高编课后作业------第十二周-Matplotlib exercise

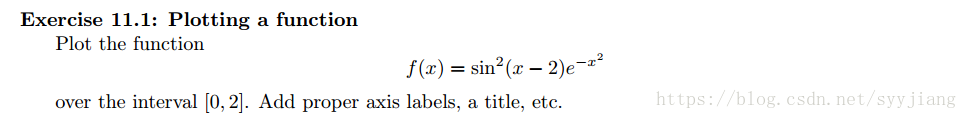
好像没有类似matlab的 syms功能（我没找），所以写了个fx

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

def fx(x):
    a = np.sin(x-2)
    a = a*a
    x = x*x
    x = -x
    x = np.exp(x)
    ret = a * x
    return ret

x = np.linspace(0,2,100)
y = fx(x)
plt.plot(x,y)
plt.xlabel('my x label')
plt.ylabel('my y label')
plt.title('exercise 1')
plt.show()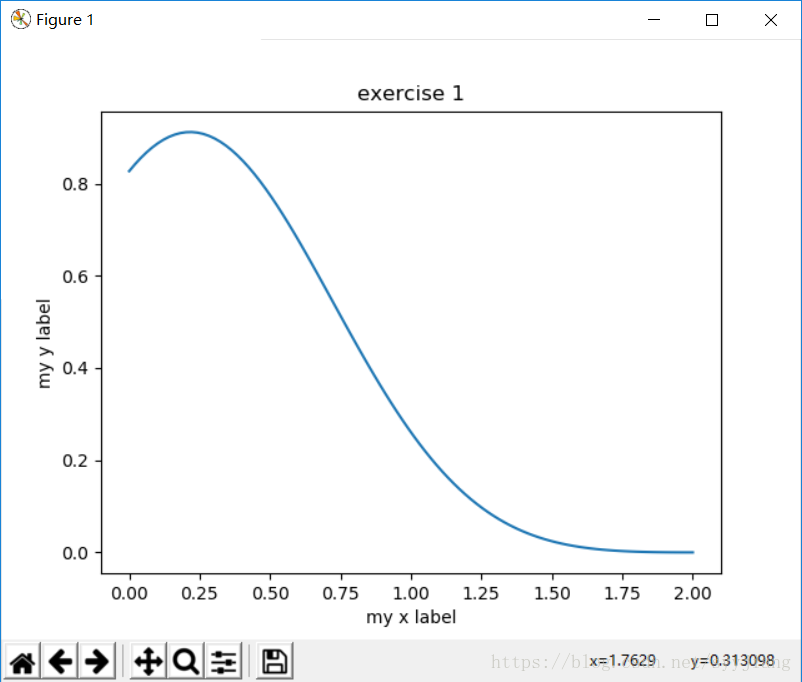

-----------------------------------------------------------------------------------------------------------------------

这题的意思大概是：X是一个对10个变量的20次观察，因此X是20*10的，每一行是1个变量的20个观测。然后生成好多b，b是10*1的，对于每一个b，生成1个z，z是标准正太分布的观测，z是20*1的，算出y。然后固定X和y，算Xb-y的最小二乘的b'，（b’就是等式左边的b箭头帽子），然后对每一组b和b’画点图就好了。 然后由于b是向量不能直接画出来，就取b的2-范数好啦。（不要在意这么多细节，关键在于如何画图）

至于实现算最小二乘，用scipy.optimize.leastsq就可以了 。。。。。于是......我就调试了将近1个小时后终于调出来了。

leastsq这个函数，传的参数主要有三个,(func, p0, args=(.....))

func是你要优化的函数，p0是迭代初始值，只要不乱选就可以。 然后p0会作为第一个参数传给func，func还可以有其他参数，那些参数通过args传给func：

比如func(p,a,b)，那leastsq(func,p0,args=(a,b))

但是！！！！这个func非常坑，要返回一个行向量而不是列向量。。。。然后另外还有一些未知错误，导致矩阵维数出错，所以最后就写成了这个鬼样子，导致p也要先reshpe一下不然ret会出错。。。。

画散点图就用scatter，贴代码：

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.optimize import leastsq


X = np.random.normal(20,2,size=(20,10))


def func(p,X,y):
    #p = p.reshape(10,1)
    """
    print(p.shape)
    print(type(p))
    print(X.shape)
    print(type(X))
    print(y.shape)
    print(type(y))
    """
    p = p.reshape(10,1)
    ret = X@p-y
    n = ret.shape[0]
    return ret.T.reshape(n)

tb = []
tbb = []
for i in range(0,8):   #生成 8 个 b
    b = np.random.normal(4,4,size=(10,1))
    z = np.random.normal(0,1,size=(20,1))
    y = X@b + z
   # print(y.shape)
    bb = leastsq(func,b,args=(X,y))[0]
    print(b.reshape(b.shape[0]))
    print(bb)
    tb.append(np.linalg.norm(b,ord=2))
    tbb.append(np.linalg.norm(bb,ord=2))

print(tb)
print(tbb)
tb = np.array(tb)
x = np.array(range(1,9))
print(x.shape)
print(tb.shape)
plt.scatter(x,tb,marker='x', label='True coefficients')
plt.scatter(x,tbb,marker='.', label='Estimated coefficients')
plt.xlabel('index')
plt.ylabel('value')
plt.legend()
plt.show()

结果大概是这个样子，还是蛮接近的，每次结果应该都不一样：

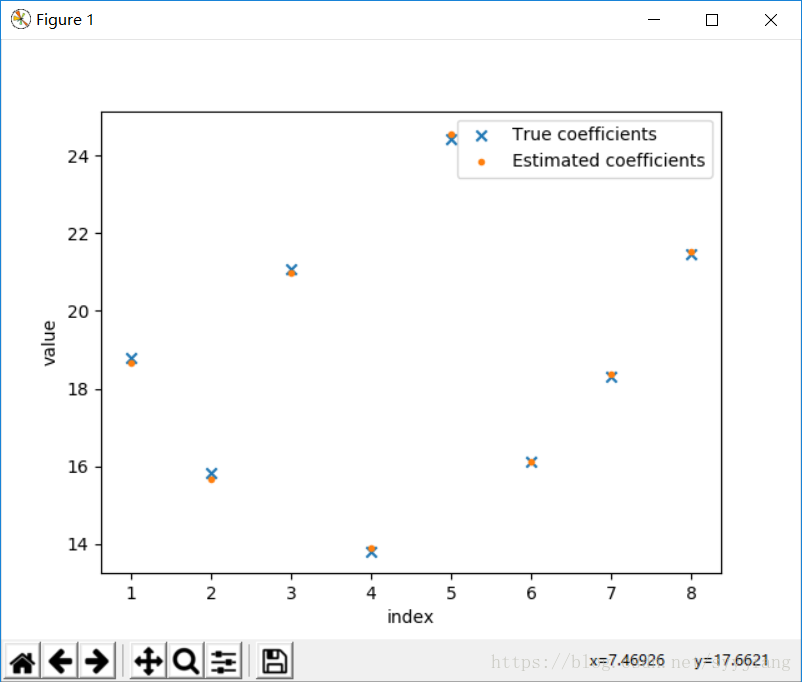
就是用高斯核密度估计来估计Z的分布，然后画直方图。这个bins意思应该是说画25个柱子。

资料好少，不过在某国外网站发现了差不多的题目，作文文档的示例：http://jpktd.blogspot.hk/2009/03/using-gaussian-kernel-density.html

import numpy as np
from scipy import stats
import matplotlib.pylab as plt
z = np.random.normal(3,4,size=(10000,))
gkde=stats.gaussian_kde(z)
ind = np.linspace(-10,20,101)
kdepdf = gkde.evaluate(ind)
plt.figure()
# plot histgram of sample
plt.hist(z, bins=25, normed=True, color='b')
# plot estimated density
plt.plot(ind, kdepdf, label='kde', color="r")
plt.title('Kernel Density Estimation')
plt.legend()
plt.show()

照猫画虎写了一个，z用的是u=3，sigma=4的正态分布。估计还是蛮准的。就是柱子不知道为什么没有边缘黑线。