P3128 [USACO15DEC]最大流Max Flow 树上差分

最新推荐文章于 2025-03-30 21:08:59 发布

原创最新推荐文章于 2025-03-30 21:08:59 发布 · 216 阅读

0 ·

CC 4.0 BY-SA版权

图论-环与根同时被 2 个专栏收录

8 篇文章

订阅专栏

倍增

2 篇文章

订阅专栏

本博客介绍了一个算法问题，即计算在一个由管道连接的隔间网络中，当进行多条牛奶运输路线时，如何找出承受最大运输压力的隔间。通过使用差分数组和LCA算法，我们能够有效地解决这个问题。

https://www.luogu.org/problem/P3128

Farmer John has installed a new system of N−1N-1N−1 pipes to transport milk between the NNN stalls in his barn (2≤N≤50,0002 \leq N \leq 50,0002≤N≤50,000), conveniently numbered 1…N1 \ldots N1…N. Each pipe connects a pair of stalls, and all stalls are connected to each-other via paths of pipes.

FJ is pumping milk between KKK pairs of stalls (1≤K≤100,0001 \leq K \leq 100,0001≤K≤100,000). For the iiith such pair, you are told two stalls sis_isi and tit_iti, endpoints of a path along which milk is being pumped at a unit rate. FJ is concerned that some stalls might end up overwhelmed with all the milk being pumped through them, since a stall can serve as a waypoint along many of the KKK paths along which milk is being pumped. Please help him determine the maximum amount of milk being pumped through any stall. If milk is being pumped along a path from sis_isi to tit_iti, then it counts as being pumped through the endpoint stalls sis_isi and

tit_iti, as well as through every stall along the path between them.

FJ给他的牛棚的N(2≤N≤50,000)个隔间之间安装了N-1根管道，隔间编号从1到N。所有隔间都被管道连通了。

FJ有K(1≤K≤100,000)条运输牛奶的路线，第i条路线从隔间si运输到隔间ti。一条运输路线会给它的两个端点处的隔间以及中间途径的所有隔间带来一个单位的运输压力，你需要计算压力最大的隔间的压力是多少。

输入格式

The first line of the input contains NNN and KKK.

The next N−1N-1N−1 lines each contain two integers xxx and yyy (x≠yx \ne yx≠y) describing a pipe

between stalls xxx and yyy.

The next KKK lines each contain two integers sss and ttt describing the endpoint

stalls of a path through which milk is being pumped.

输出格式

An integer specifying the maximum amount of milk pumped through any stall in the

barn.

输入输出样例

输入 #1复制

输出 #1复制

给你m个操作，问你每次在(p,q)路径上给所有点的权值+1，问你最后点的权值最大
我们考虑差分

首先在p上面对差分数组+1，再在q上面对差分数组+1，在Lca(p,q)处对差分数组-1,Lca(p,q)的父亲差分-1

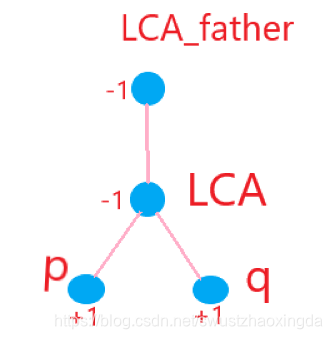
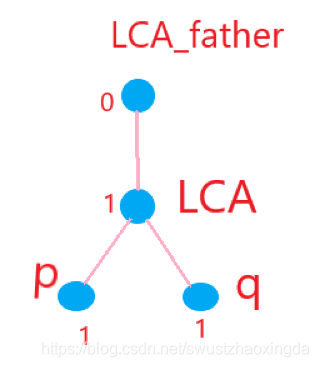
然后倍增LCA差分求和，就没了

#include<bits/stdc++.h>

using namespace std;
const int maxn=2e5+10;
typedef long long ll;
struct EDGE
{
    int x,y,nxt;
};
EDGE edge[maxn];
int head[maxn];
int deep[maxn];
int father[maxn][20];
int val[maxn];
int tot;
int sum[maxn];
int ans;
void init()
{
    tot=0;
    memset(head,-1,sizeof(head));
    memset(edge,0,sizeof(edge));
    deep[0]=0;
    memset(sum,0,sizeof(sum));
    memset(val,0,sizeof(val));
    ans=0;
}
void add(int x,int y)
{
    edge[tot].x=x;
    edge[tot].y=y;
    edge[tot].nxt=head[x];
    head[x]=tot;
    tot++;
}
void dfs(int x,int fa)
{
    father[x][0]=fa;
    deep[x]=deep[fa]+1;
    for(int j=1;j<20;j++)
    {
        father[x][j]=father[father[x][j-1]][j-1];
    }
    for(int i=head[x];i!=-1;i=edge[i].nxt)
    {
        if(edge[i].y!=fa)
        {
            dfs(edge[i].y,x);
        }
    }
}
int lca(int x,int y,int n)
{
    if(deep[x]<deep[y])
        swap(x,y);
    for(int i=19;i>=0;i--)
    {
        if(deep[x]-(1<<i)>=deep[y])
            x=father[x][i];
    }
    if(x==y)
        return x;
    for(int i=19;i>=0;i--)
    {
        if(father[x][i]!=father[y][i])
        {
            x=father[x][i];
            y=father[y][i];
        }
    }
    return father[x][0];
}
void dfs2(int x,int fa)
{
    sum[x]=val[x];
    for(int i=head[x];i!=-1;i=edge[i].nxt)
    {
        if(edge[i].y!=fa)
        {
            dfs2(edge[i].y,x);
            sum[x]+=sum[edge[i].y];
        }
    }
    ans=max(sum[x],ans);
}
int main()
{
    int n,m,x,y;
    init();
    scanf("%d%d",&n,&m);
    for(int i=0;i<n-1;i++)
    {
        scanf("%d%d",&x,&y);
        add(x,y);
        add(y,x);
    }
    dfs(1,0);
    while(m--)
    {
        scanf("%d%d",&x,&y);
        int LCA=lca(x,y,n);
        val[x]++;
        val[y]++;
        val[LCA]--;
        val[father[LCA][0]]--;
    }
    dfs2(1,0);
    cout<<ans;
    return 0;
}