刷题收获记录-盛最多水的容器

# 问题描述        

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例 1：

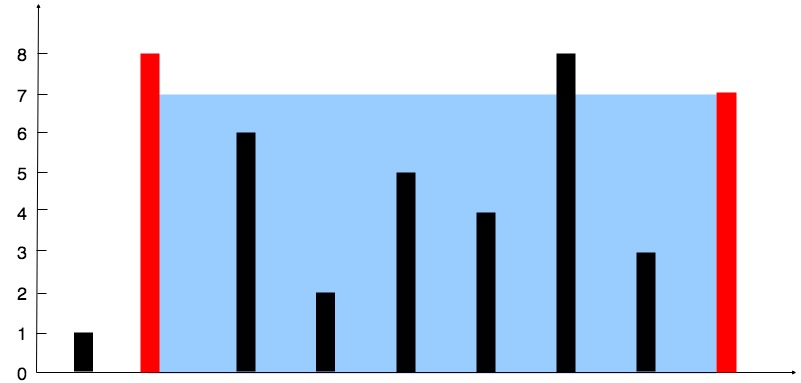
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

提示：

• n == height.length
• 2 <= n <= 105
• 0 <= height[i] <= 104

刷题前言

        看到题目一头雾水，只知道面积怎么计算。随后慢慢分析题目，既然要求最大面积，先观察特点。当宽度最大的时候，面积由最短边决定。那么宽度小于最大边后，面积由高决定了，一下子就明了了。既然最后分析，面积由高决定了，那么就将两条边从头部和尾部不断找出最大边即可。也就是height[l]跟height[r]谁大，小的就推进。

解题步骤

第一步：找到最短边

int minHeight = Math.min(height[l],height[r]);

第二步：小边推进

if (height[l] < height[r]){
    l++;
}else {
    r--;
}

完整代码

public static int maxArea(int[] height){
        int l = 0;
        int r = height.length - 1;
        int maxArea = 0;
        while (l < r){
            int minHeight = Math.min(height[l],height[r]);
            int area = (r - l) * minHeight;
            maxArea = Math.max(area,maxArea);
            if (height[l] < height[r]){
                l++;
            }else {
                r--;
            }
        }
        return maxArea;
    }

        虽然说做出来了，但是一个优秀的程序员，应该要做到，做出来后返回去思考一下是否还存在优化空间。从上面不难看出，当最短边推进后，如果推进后的边比当前最短边还短，那么就可以不需要再次进行计算面积了。这里就是优化，那么就需要记录最短边，减少计算。

优化后代码

public static int maxArea(int[] height){
        int l = 0;
        int r = height.length - 1;
        int maxArea = 0;
        while (l < r){
            int minHeight = Math.min(height[l],height[r]);
            int area = (r - l) * minHeight;
            maxArea = Math.max(area,maxArea);
            while (l < r && height[l] <= minHeight){
                l++;
            }
            while (l < r && height[r] <= minHeight){
                r--;
            }
        }
        return maxArea;
    }

总结

        这个问题是一类双指针问题，解决这类问题的时候，没有思路的话就从已知入手。比如这道题，已知的就是面积计算，然后围绕公式进行。定一个不用去考虑的变量，如宽，接下来就是考虑高如何进行。

        解决完后，需要对代码进行再次检验，查看是否存在可优化空间。

--题目来自力扣 LeetCode