136.137.260. Single Number && 位运算

136.137.260. Single Number && 位运算

 

 

136. Single Number

 

意思就是给你一堆数，每个数都出现了两次，只有一个数只出现了一次，找出这个数

位运算（和c艹一样）

&：按位与

|：按位或

^：异或（一样为0，不一样为1）

再说一下异或的性质，满足交换律和结合律

因此：

　　对于任意一个数n

　　n ^ 0 = n

　　n ^ n = 0

　　对于这道题来说，所有数依次异或剩下的就是那个数了

 　　

1 class Solution(object):
2     def singleNumber(self, nums):
3         ans = 0
4         for i in nums:
5             ans ^= i
6         return ans

 

 

127. Single Number II

意思就是所有的数都出现了三遍，只有一个数出现了一遍，求这个数

这个题没明白位运算怎么算的

对于给定数组nums，剔除所有重复元素后为nums'，要求答案ans，则有sum（nums）*3 - sum（num） = 2 * ans

则有表达式(int)((3*sum(set(nums)) - sum(nums)) / 2)

　　

1 class Solution:
2     def singleNumber(self, nums):
3         return (int)((3*sum(set(nums)) - sum(nums)) / 2)

 

 

260. Single Number III

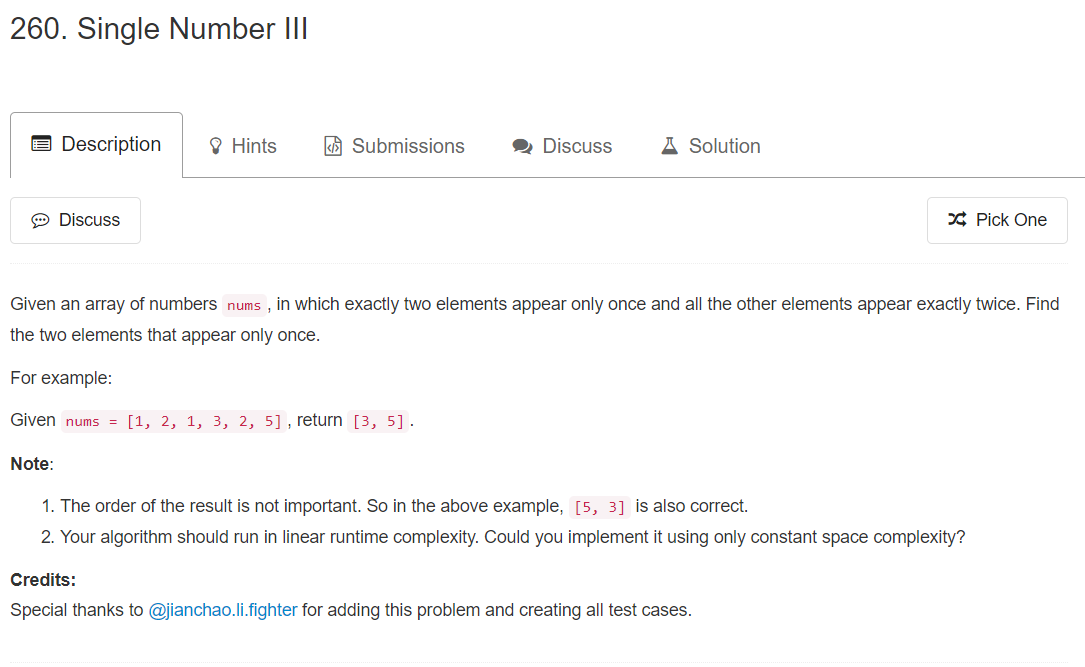
给你一个数组，所有的数都出现了两边，有两个数出现了一遍，找出这两个数

思路是，只要把这两个数m，n分到不同的两组中，就转化为了第一个问题

对于这道题来说，不需要真正的找到这两个数，只需要找出不同就行了

我们先把所有数异或起来，那么结果就是m ^ n，那么我们找到这个m ^ n的lowbit（不知道的你或许该看看树状数组？？？）

那么m，n的lowbit一定不一样，所以lowbit为1的和m异或，lowbit为0的和n异或就完成了

那么我们不用管其他数，因为对于两个一样的数，他们的等价的lowbit上一定一样，所以势必会被分到同一组

这个看代码更容易理解

 1 class Solution:
 2     def singleNumber(self, nums):
 3         A = 0
 4         B = 0
 5         diff = 0
 6         length = len(nums)
 7         for i in range(length):
 8             diff ^= nums[i]
 9         lowbit = diff & (-diff)
10         for i in range(length):
11             if (nums[i] & lowbit) != 0:
12                 A ^= nums[i]
13             else:
14                 B ^= nums[i]
15         return [A,B]

 

 

 

 

 

 

 

 

posted @ 2018-02-01 13:16 swallowblank 阅读(...) 评论(...) 编辑 收藏