day20SVD奇异值分解，降维数据集

原创已于 2025-05-19 22:23:02 修改 · 892 阅读

29 ·

CC 4.0 BY-SA版权

文章标签：

#python #机器学习 #算法

于 2025-05-19 22:22:30 首次发布

python打卡练习专栏收录该内容

20 篇文章

订阅专栏

线性代数里面学过

进一步的，通过特征值，特征向量，有可能存在一个可逆阵P或者正交阵Q，使得：

A=PDP-1 其中D是对角矩阵，对角线元素为A的特征值，P为相似变换阵，列向量为A特征向量。

A=QDQT 其中D是对角矩阵，对角线元素为A的特征值，Q为正交相似变换阵容，列向量为A特征向量经线性变换后的正交向量。

总之，A可以通过特征值，特征向量进行分解，但是存在前提，A可以相似对角化，或者A是实对称矩阵（一定可以对角化），A是方阵（大前提！）这存在诸多约束，在机器学习，深度学习中，面对的dataframe往往并不满足以上条件，因此，有必要了解SVD奇异值分解，通过关于A的奇异值以及特征向量进行任意矩阵的分解。下面为公式：

设A为m*n矩阵

U m*m（左奇异向量矩阵）：为一个正交矩阵，其列向量为AAT的特征向量。表示原始矩阵 A 在行空间（样本空间）中的主方向或基向量。简单来说，U 的列向量描述了数据在行维度上的“模式”或“结构”。

Σ m*n（奇异值矩阵）：为一个m*n的对角阵，对角线元素为奇异值，通对 ATA 或 AAT 的特征值取平方根得到的。奇异值表示原始矩阵 A 在每个主方向上的“重要性”或“能量”。较大的奇异值对应更重要的特征，较小的奇异值对应噪声或次要信息。

VT n*n（右奇异向量矩阵的转置）：为一个正交矩阵，其行向量（注意有转置，即V的列向量）为ATA的特征向量。表示原始矩阵 A 在列空间（特征空间）中的主方向或基向量。简单来说，V 的列向量描述了数据在列维度上的“模式”或“结构”。

主要应用：
- 降维：通过保留前 k 个奇异值及其对应的 U 和 V 的列向量，可以近似重构 A，减少数据维度（如 PCA 的基础）。
- 数据压缩：如图像压缩，丢弃小的奇异值以减少存储空间。
- 去噪：小的奇异值往往对应噪声，丢弃它们可以提高数据质量。
- 推荐系统：如矩阵分解，用于预测用户评分矩阵中的缺失值。

实际数据降维中，我们是否可以通过保留前k个奇异值，去U/V的前k列元素，来保留数据集中更重要的特征，忽略贡献少或者是噪声的特征。

通过一个例子，重构A矩阵，并计算损失，验证假设是否成立。

import numpy as np

A = np.array([[1, 2, 3],
              [4, 5, 6],
              [7, 8, 9],
              [10, 11, 12],
              [13, 14, 15]])

print("A的形状为：", A.shape)  # 输出：(5, 3)

u_display,sigma_display,vT_display = np.linalg.svd(A,full_matrices=False)

print("u的形状为：", u_display.shape)  # 输出：(5, 3)
print("sigma的形状为：", sigma_display.shape)  # 输出：(3,)
print("v的形状为：", vT_display.shape)  # 输出：(3, 3)

k = 1
u_display_reduced = u_display[:, :k]
sigma_display_reduced = np.diag(sigma_display[:k])
vT_display_reduced = vT_display[:k, :]

A_reduced = u_display_reduced @ sigma_display_reduced @ vT_display_reduced

print("重构后A表示为：", A_reduced)
error = np.linalg.norm(A - A_reduced)/np.linalg.norm(A,'fro')
print("重构误差为：", error)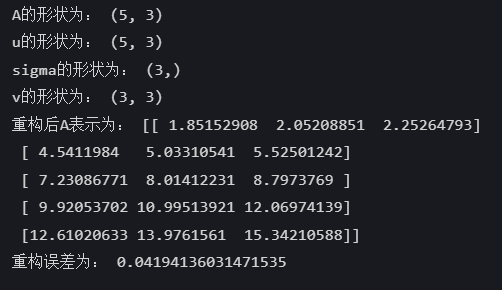

观察可以看到重构后A元素值变化波动不大，且损失也只有4.19%，处于可接受的范围。

接下来使用SVD对机器学习中的训练集和测试集进行数据的降维。

#划分训练集和测试集
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.2,random_state=42)

#对数据进行标准化，SVD一般要先标准化。
scaler = StandardScaler()
x_train_scaled = scaler.fit_transform(x_train)
x_test_scaled = scaler.transform(x_test)

#训练集的SVD分解
#假设x_train_scaled的形状为(m,n)，其中m是样本数，n是特征数
#full_matrices=False表示只计算前n个奇异值和奇异向量，使得u.shape == (m,n),sigma.shape == (n,),vT.shape ==(n,m)
u_train,sigma_train,vT_train = np.linalg.svd(x_train_scaled,full_matrices= False)

#保存前k个奇异值
k = 10
#保留vT_train的前k行
vT_train_reduced = vT_train[:k,:]
u_train_reduced = u_train[:,:k]

#训练集的降维
x_train_reduced = x_train_scaled @ vT_train_reduced.T

print(f'降维前训练集形状：{x_train_scaled.shape}') 
print(f'降维后训练集形状：{x_train_reduced.shape}')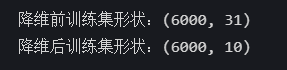

可以看到，特征数已经从31变为了10。这里，在编码时我产生过一个错误，正如上图

既然奇异值分解的公式如此，为什么降维时，代码输入如下时却没有降维效果。

x_train_reduced = u_train_reduced @ np.diag(sigma_train[:k]) @ vT_train_reduced

这是因为，保留前10个奇异值后，u_train_reduced为6000*10的矩阵（保留前10列），vT_train_reduced为10*31的矩阵（保留前10行），sigma_train[:k]为10*10的矩阵。根据矩阵乘法，这个表达式最后是重构了矩阵x_train_scaled。

因此，在实现数据特征降维时，应该是x_train_scaled@vT_train_reduced.T。这计算每个样本在这 k 个主成分上的坐标，得到降维后的数据。

x_train_reduced = x_train_scaled@ vT_train_reduced.T

我们也可以用

x_train_reduced = u_train_reduced @ np.diag(sigma_train[:k])

这两者时等价，根据上面的分解公式，x_train_scaled（即A）可以用 u_train @ sigma_train @ vT_train表示，也可近似用 x_train_scaled=u_train_reduced @ np.diag(sigma_train[:k]) @ vT_train_reduced表示，两边同时乘vT_train_reduced.T后，x_train_scaled@vT_train_reduced.T=u_train_reduced @ np.diag(sigma_train[:k]) （vT_train_reduced@vT_train_reduced.T为单位阵）

注意，对训练集做了降维处理后，训练集只有10个特征去训练，那么测试集在模型预测时也只能有10个特征，并且，为了保证训练数据的特征映射规则，测试数据也能遵循相同的规则，二者共用相同的低维映射矩阵vT_train_reduced.T。

x_test_reduced = x_test_scaled  @ vT_train_reduced.T

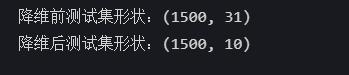
print(f'降维前测试集形状：{x_test_scaled.shape}')
print(f'降维后测试集形状：{x_test_reduced.shape}')

@浙大疏锦行