数据结构（一）

时间复杂度和空间复杂度

算法中的基本操作的执行次数，为算法的时间复杂度。

空间复杂度计算规则基本跟时间复杂度类似，也使用大O渐进表示法。

线性表

顺序表

顺序表是用一段物理地址连续的存储单元依次存储数据元素的线性结构，一般情况下采用数组存储。在数组 上完成数据的增删查改。

顺序表分为：静态顺序表：使用定长数组；动态顺序表：动态的开辟数组存储。

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
//#ifndef __SEQLIST_H_
//#define __SEQLIST_H_
//#endif 


//静态稍规范的顺序表
#define N 10
typedef int SLDataType;
struct SeqList
{
	SLDataType a[N];
	int size;    //顺序表的大小
};

typedef int SLDataType;
typedef struct SeqList
{
	SLDataType* arr;
	int size;        //数组的大小
	int capacity;   //存储空间的大小
}SL;
void SLInit(SL* ps1)
{
	assert(ps1);
	ps1->arr = NULL;
	ps1->capacity = ps1->size = 0;
}
void SLDestroy(SL* psl)
{
	assert(psl);
	if (psl->arr)
	{
		free(psl->arr);
		psl->arr = NULL;
		psl->capacity = psl->size = 0;
	}
}

//打印SL
void SLPrint(SL* psl)
{
	assert(psl);
	for (int i = 0; i < psl->size; ++i)
	{
		printf("%d  ", psl->arr[i]);
	}
	printf("\n");
}
//一个扩容函数
void CheckCapacity(SL* psl)
{
	assert(psl);

	if (psl->capacity ==  psl->size)
	{
		//当size和容量一样大的时候需要扩容
		int NewCapacity = psl->capacity;
		NewCapacity = NewCapacity == 0 ? 4 : NewCapacity * 2;
		//有两种扩容方式，1、原地扩容(后面堆的空间足够)；2、异地扩容(后面空间不够,去堆的其他 地方开辟连续空间)；
		SLDataType* Tmp = (SLDataType*)realloc(psl->arr, sizeof(SLDataType) * NewCapacity);
		if (Tmp == NULL)
		{
			perror("realloc error");
			exit(-1);
		}
		psl->arr = Tmp;
		psl->capacity = NewCapacity;
	}
}

//增删查改
//头查头删，尾插尾删
void SLPsuhBack(SL* psl, SLDataType data)
{
	assert(psl);
	CheckCapacity(psl);
	psl->arr[psl->size] = data;
	psl->size++;
	//也可以使用插入数据的，在最后插入
	//
	//SLInsert(psl, (psl->size), data);
}
//头部插入数据，需要将数据挪动，复杂度为O(N)
void SLPushFront(SL* psl, SLDataType data)
{
	assert(psl);
	CheckCapacity(psl);
	int end = psl->size;
	while (end > 0)
	{
		psl->arr[end] = psl->arr[end - 1];
		end--;
	}
	psl->arr[0] = data;
	psl->size++;

	//也可以使用插入实现
	//SLInsert(psl, 0, data);
}
//尾部弹出数据
void SLPopBack(SL* psl)
{
	比较温柔的检查数据
	//assert(psl);
	//if (psl->size > 0)
	//{
	//	psl->size--;
	//}
	//else
	//	return;

	//比较暴力的检查数据，告诉你出错的地方在哪儿
	assert(psl->size > 0);
	psl->size--;


}
//从头部弹出数据
void SLPopFront(SL* psl)
{
	assert(psl->size>0);
	//记得检查一下size的大小
	assert(psl->size > 0);
	int end = psl->size;
	for (int i = 0; i < end - 1; i++)
	{
		psl->arr[i] = psl->arr[i + 1];
	}
	psl->size--;
}

//查找数据
int SLFind(SL* psl, SLDataType data)
{
	assert(psl);
	int i = 0;
	for (i = 0; i < psl->size; i++)
	{
		if (data == psl->arr[i])
		{
			return i;
		}
	}
	return -1;
}

void SLInsert(SL* psl,size_t pos, SLDataType data)
{
	assert(psl);
	assert(pos <= psl->size);
	CheckCapacity(psl);
	//将数据往后挪动
	//int end = psl->size-1;
	//while (end >=(int) pos)   //不加（int）的时候，当pos为0的时候因为pos是size_t类型的，在0位置插入的时候，会发生整型提升，
	//					         //把有符号数转换为一个无符号数去比较，所以负数的时候，会继续进入循环
	//{
	//	psl->arr[end+1] = psl->arr[end];
	//	end--;
	//}
	int end = psl->size ;
	while (end > pos)   
	{
		psl->arr[end] = psl->arr[end-1];
		end--;
	}
	psl->arr[pos] = data;
	psl->size++;
}

void SLErase(SL* psl, size_t pos)
{
	assert(psl);
	assert(pos <= psl->size);
	//将指定位置的数据进行覆盖即可
	for (int i = pos-1; i < psl->size; i++)
	{
		psl->arr[i] = psl->arr[i + 1];
	}
	psl->size--;
}
//顺序表的修改
void SLModify(SL* psl, size_t pos, SLDataType data)
{
	assert(psl);
	assert(pos < psl->size);
	psl->arr[pos] = data;
}

链表

链表是一种物理存储结构上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链 接次序实现的 。主要有单向，双向，带头，不带头，循环，非循环这几种结构。最常用的是无头单向非循环链表，例如哈希桶和图的邻接表等等；其次是带头双向循环链表。

typedef int SLTDataType;
typedef struct SListNode {
	SLTDataType data;
	struct SListNode* next;    //下一个结构体的指针
}SLTNode;
 


//销毁链表
void SlistDestroy(SLTNode** phead)
{
	assert(phead);
	while (*phead != NULL)
	{
		SListPopFront(phead);
	}
	*phead = NULL;
}
void SListPrint(SLTNode*  phead)
{
	SLTNode* cur = phead;
	while(cur != NULL)
	{
		printf("-->%d", cur->data);
		cur = cur->next;
	}
	printf("-->NULL\n");
}

//创造节点
SLTNode* BuyNewNode(SLTDataType x)
{
	//创建一个新的节点，需要在堆上创造，否则临时变量在函数结束后会被销毁
	SLTNode* newnode = (SLTNode*)malloc(sizeof(SLTNode));
	newnode->data = x;
	newnode->next = NULL;
	return newnode;
}

//打印链表
void SListPrint(SLTNode* phead)
{
	SLTNode* cur = phead;
	while(cur != NULL)
	{
		printf("-->%d", cur->data);
		cur = cur->next;
	}
	printf("-->NULL\n");
}

//头插链表Node
//这里使用二级指针的原因是：需要phead指针的地址，
// 指向上一个节点的地址，如果用一级指针的话，只是值传递，不会修改指针的地址
void SListPushFront(SLTNode** phead)
{
	assert(pphead);
	SLTNode* newnode = BuyNewNode(x);
	newnode->next = *pphead;
	*pphead = newnode;
}
//尾插
//尾插也需要二级指针，需要考虑是否为一个空链表，如果是一个空链表的话，就必须改变plist的值
void SListPushBack(SLTNode** pphead)
{
	assert(pphead);
	SLTNode* backnode = BuyNewNode(x);
	if (*pphead == NULL)
	{
		*phead = backnode;
	}
	else
	{
		SLTNode* cur = *pphead;
		while (cur->next != NULL)
		{
			cur = cur->next;
		}
		cur->next = backnode;
	}
}
//尾删
void SListPopBack(SLTNode** pphead)
{
	assert(pphead);
	assert(*pphead);
	if ((*pphead)->next == NULL)
	{
		free(*pphead);
		*pphead = NULL;
	}
	else
	{
		SLTNode* cur = *pphead;
		写法1：
		//SLTNode* cur1 = NULL;
		//while (cur->next != NULL)
		//{
		//	cur1 = cur;
		//	cur = cur->next;
		//}

		//cur1->next = NULL;
		//free(cur);
		//cur = NULL;
		//写法2
		while (cur->next->next != NULL)
		{
			cur = cur->next;
		}
		free(cur->next);
		cur->next = NULL;
	}
}
//头删
void SListPopFront(SLTNode** pphead)
{
	assert(pphead);
	if (*pphead == NULL)
	{
		return;
	}
	else
	{
		SLTNode* cur = *pphead;
		*pphead = (*pphead)->next;		//*pphead = cur->next; 
		free(cur);
		cur = NULL;	
	}
}
//查找
SLTNode* SListFind(SLTNode** pphead,SLTDataType x)
{

    assert(pphead);
	SLTNode* cur = *pphead;
	while (cur!= NULL)
	{
		if (cur->data != x)
		{
			cur = cur->next;
		}
		else
		{
			return cur;
		}
	}
	return NULL;
}
//在pos前插入
void SListInsert(SLTNode** pphead, SLTNode* pos, SLTDataType x)
{
    assert(pphead);
	assert(pos);
	SLTNode* prev = *pphead;
	//要注意头插的情况
	if (pos == pphead)
	{
		SListPushFront(pphead, x);
	}

	else
	{
		while (prev->next != pos)
		{
			prev = prev->next;
		}
		SLTNode* newnode = BuyNewNode(x);
		prev->next = newnode;
		newnode->next = pos;
	}
}
//在pos后面c插入
void SListInsertBack(SLTNode* pos, SLTDataType x)
{
	SLTNode* newnode = BuyNewNode(x);
	newnode->next = pos->next;
	pos->next = newnode;
}

//删除pos
void SListErase(SLTNode** pphead, SLTNode* pos)
{
	assert(pphead);
	assert(pos);
	SLTNode* prev = *pphead;
	//判断是否删除的是头部位置
	if (pos == *pphead)
	{
		SListPopFront(pphead);
	}
	else
	{
		while (prev->next != pos)
		{
			prev = prev->next;
			//检测pos是否为空节点
			assert(prev);
		}
		prev->next = pos->next;
		free(pos);
	}
}
//删除pos后面的位置
void SListEraseBack(SLTNode* pos)
{
	assert(pos);
	//需要判断是不是尾部
	if (pos->next == NULL)
	{
		return;
	}
	else
	{
		SLTNode* next1 = pos->next;
		pos->next = next1->next;
		free(next1);
	}
}

顺序表优点：1、尾插尾删效率高；2、随机访问(用下标随机访问)；3、相比链表而言，cpu高速缓存命中率较高。缺点：头部删除和中部插入删除效率很低--O(N)，扩容性能消耗(异地扩容)+空间浪费。

链表优点：1、任意位置插入删除效率很高-O(1)；2、按需申请释放，不存在浪费空间。缺点：不能随机访问

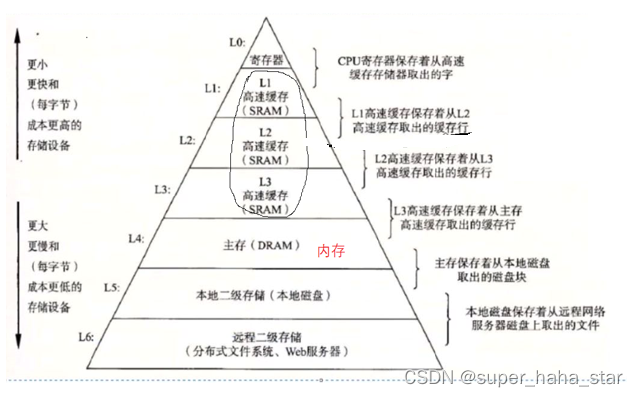
 CPU执行指令，不会直接访问内存，首先看数据在不在三级缓存(L1,L2,L3)，在的话直接访问，如果不在的话，则加载到缓存(L1,L2,L3)在由CPU获取。加载进入三级缓存的时候，连续的内存位置会被一起加载进去(CPU的加载策略)，加载的长度取决与硬件，对于内存不连续的链表，加载内存的时候，容易造成缓存污染。

栈和队列

栈：先进后出，常用函数size(),top(),push(),pop()，栈的实现一般可以使用数组或者链表实现，相对而言数组的结构实现更优一些。因为数组在尾上插入数据的代价比较小。

typedef int STDataType;
typedef struct Stack
{
	STDataType* a;
	int top;
	int capacity;
}ST;
void StackInit(ST* ps)
{
	assert(ps);
	ps->a = NULL;
	ps->capacity = ps->top = 0;
}
void StackDestroy(ST* ps)
{
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->capacity = ps->top = 0;
}
void StackPush(ST* ps, STDataType x)
{
	assert(ps);
	//扩容
	if (ps->capacity == ps->top)
	{
		int NewCapacity = (ps->capacity == 0) ? 4 : ps->capacity * 2;
		STDataType* temp = (STDataType*)realloc(ps->a, NewCapacity * sizeof(STDataType));
		if (temp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		ps->capacity = NewCapacity;
		ps->a = temp;
	}
	ps->a[ps->top] = x;
	ps->top++;
}
void StackPop(ST* ps)
{
	assert(ps);
	assert(!StackEmpyt(ps));
	ps->top--;
}
STDataType StackTop(ST* ps)
{
	assert(ps);
	assert(!StackEmpyt(ps));
	return ps->a[ps->top - 1];
}
bool StackEmpyt(ST* ps)
{
	assert(ps);
	return ps->top == 0;
}
int STackSize(ST* ps) 
{
	assert(ps);
	return ps->top;
}

队列：先进先出，常用函数front(),back(),push(),pop()。队列：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出 FIFO(First In First Out) 入队列：进行插入操作的一端称为队尾 出队列：进行删除操作的一端称为队头。队列也可以数组和链表的结构实现，使用链表的结构实现更优一些，因为如果使用数组的结构，出队列在数 组头上出数据，效率会比较低。

typedef int QDataType;

typedef struct QueueNode
{
	struct QueueNode* next;
	QDataType val;

}QNode;
typedef struct Queue
{
	QNode* head;
	QNode* tail;
	int size;

}Queue;
void  QueueInit(Queue* pq)
{
	assert(pq);
	pq->head = pq->tail = NULL;
	pq->size = 0;

}
void QueueDestroy(Queue* pq)
{
	assert(pq);
	QNode* cur = pq->head;
	while (cur)
	{
		QNode* del = cur;
		cur = cur->next;
		free(del);
	}
	pq->head = pq->tail = NULL;
}
void QueuePush(Queue* pq, QDataType x)
{
	assert(pq);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode==NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	else
	{
		newnode->val = x;
		newnode->next = NULL;
	}
	//开始往队列里塞入数据，首先判断是否为空
	if (pq->head == NULL)
	{
		pq->head = pq->tail = newnode;

	}
	else
	{
		pq->tail->next = newnode;
		pq->tail = newnode;
	}
	pq->size++;

}
void QueuePop(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(&pq));
	if (pq->head->next == NULL)
	{
		free(pq->head);
		pq->head = pq->tail = NULL;
	}
	else
	{
		QNode* del = pq->head;
		pq->head = pq->head->next;
		free(del);

	}
	pq->size--;
}
QDataType QueueFront(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(&pq));
	return pq->head->val;

}
QDataType QueueBack(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(&pq));

	return pq->tail->val;
}
bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->head == NULL && pq->tail == NULL;
}
int QueueSize(Queue* pq)
{
	assert(pq);
	return pq->size;
}