2、基于框架Hierarchical Softmax的模型
下面介绍基于Hierarchical Softmax的两个模型——CBOW模型和Skip-gram模型。两者的结构如下:
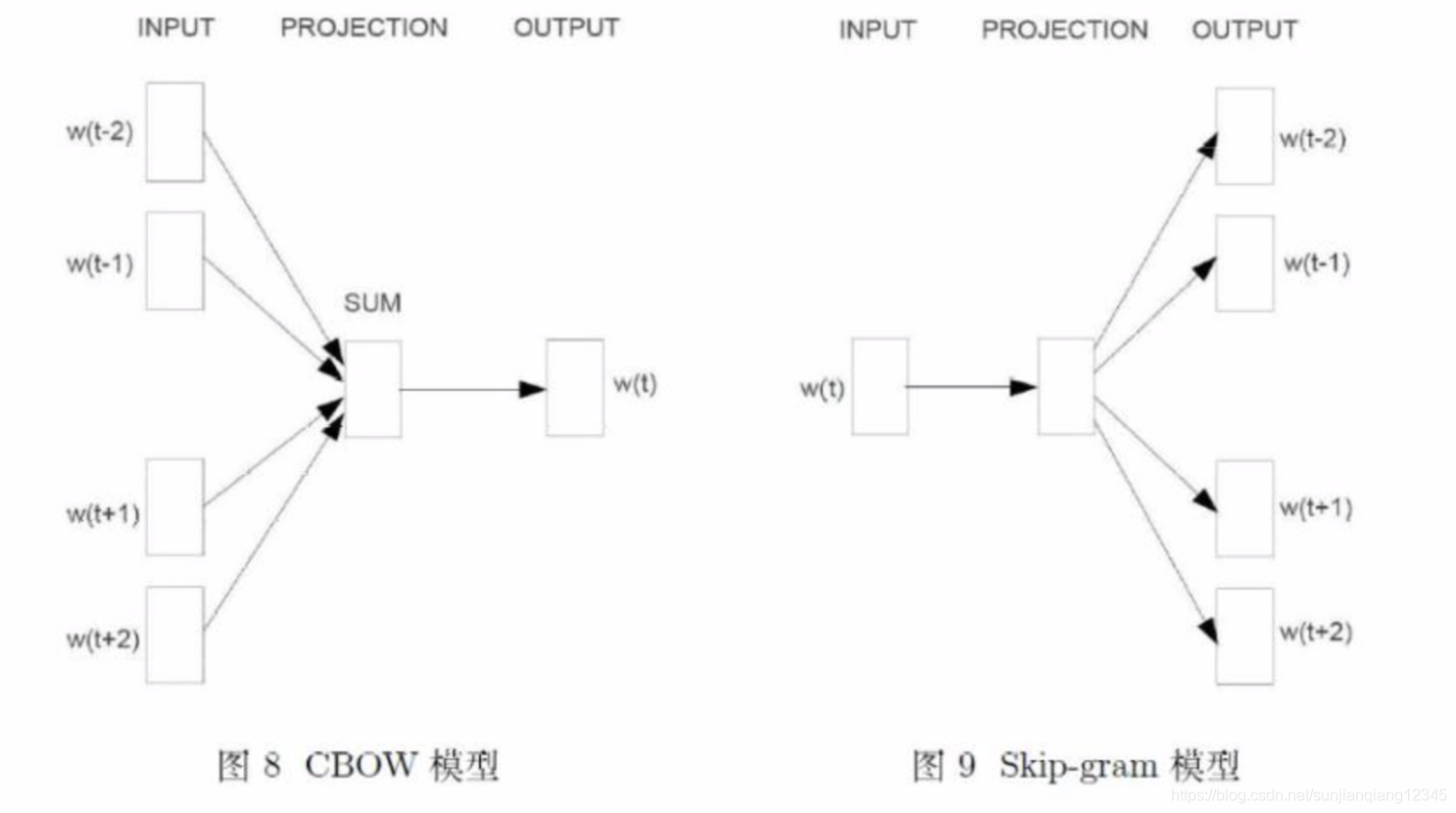
两个模型都包含三层:输入层、投影层和输出层。前者是在已知当前词的上下文(context)
的前提下,预测当前词
;后者是在已知当前词
的前提下,预测其上下文
。CBOW模型的目标函数是对数似然函数
其中为
函数。Skip-gram模型的目标函数也是对数似然函数
。
(1)CBOW模型
① 网络结构
CBOW模型的网络结构包括三层:输入层、投影层和输出层。以为例:
a 输入层: 包含中
个词的词向量
,其中
为词向量的长度。
b 投影层:将输入层的个词向量求和累加,即
。
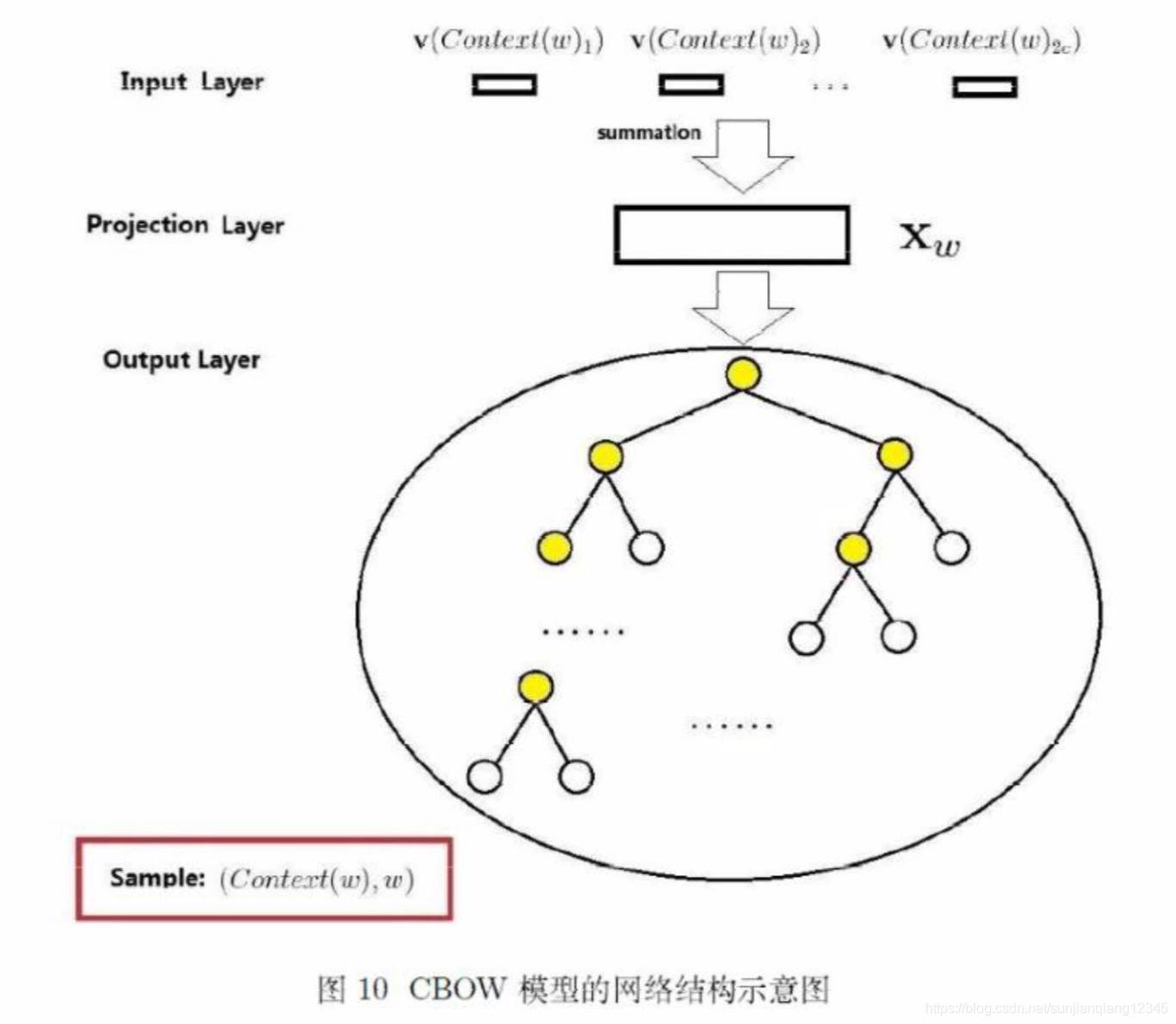
c 输出层:输出对应一棵二叉树,它是以语料中出现过的词当叶子结点,以各词在语料中出现的次数当权值构造出来的Huffman树。该树的叶子结点共个,分别对应词典
中的词。
② 梯度计算及参数更新公式
考虑Huffman树中的某个叶子结点,假设它对应词典中的词
,记
a、:从根结点出发到达
对应叶子结点的路径;
b、:路径
中包含结点的个数;
c、:路径
中的
个结点,其中
表示根结点,
表示词
对应的结点;
d、: 词
的Huffman编码,它由
位编码构成,
表示路径
中第
个结点对应的编码(根结点不对应编码)。
e、: 路径
中非叶子结点对应的向量,
表示路径
中第
个非叶子结点对应的向量。
以“足球”为例。如下图,红线表示路径
,长度为
。
为路径
上的5个结点。
分别为1,0,0,1,
为路径
上4个非叶子结点对应的向量。
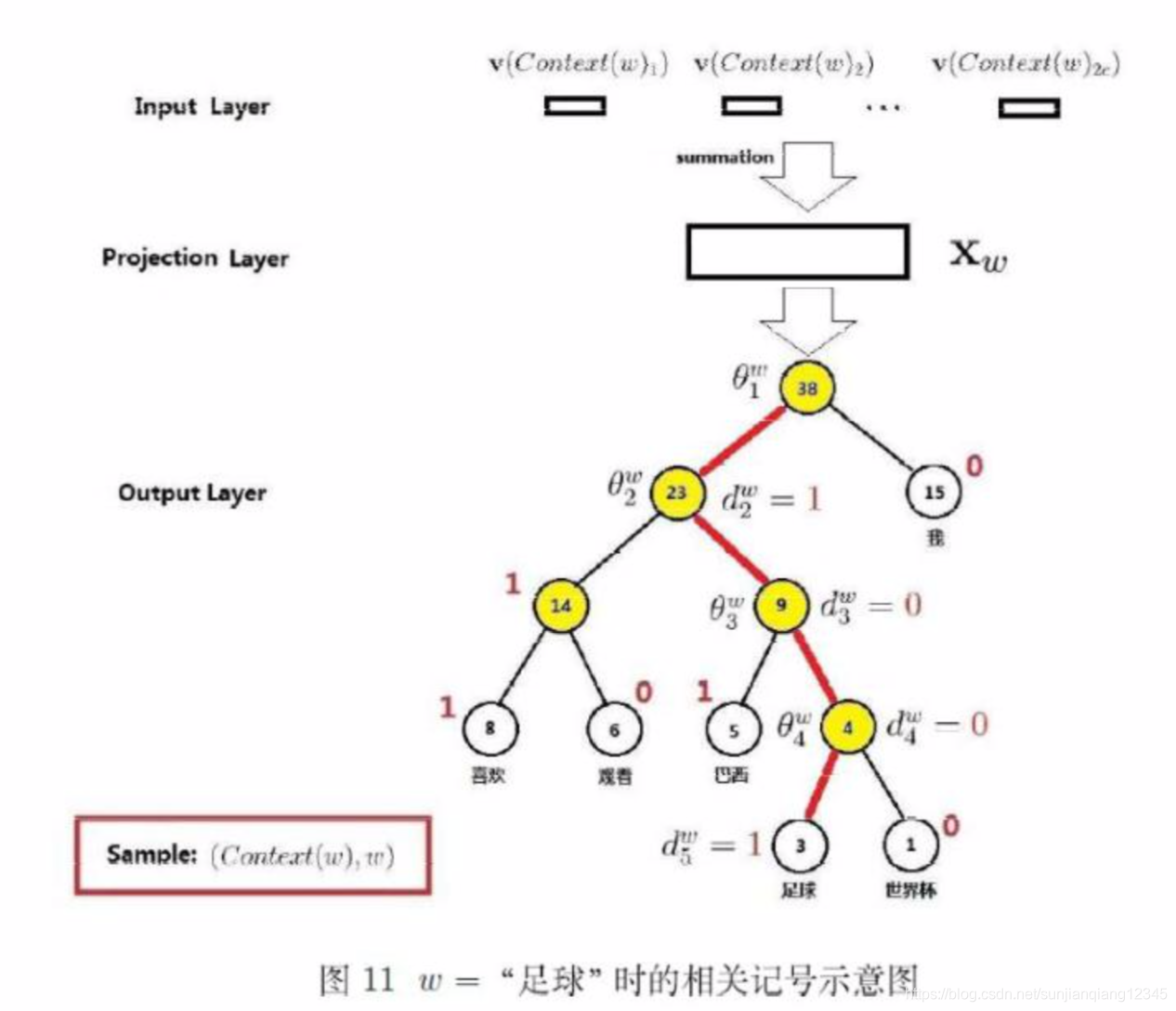
条件概率函数的计算。从根结点到达“足球”这个叶子结点,中间经历了4次分支,每一次分支都可视为进行了一次二分类。在word2vec中约定:
即将一个结点进行分类时,分到左边的是负类,分到右边的是正类。一个结点被分为正类和负类的概率分别为
和
所以上述4个二分类的概率如下:
1、第1次:;
2、第2次:;
3、第3次:;
4、第4次:,
所以
总结:对于字典中的任何词
,Huffman树中必有从根结点到词
对应结点的路径
。
上存在
个分支,将每个分支看作一次二分类,每一次分类产生一个概率,将这些概率乘起来,就是
,即
其中
损失函数取对数似然函数:
![]()
设大括号中的连加项为:
![]()
然后使用随机梯度上升法来更新参数:每取一个样本, 对目标函数中的所有参数做一次刷新。目标函数
中的参数包括向量
.
关于
的梯度为
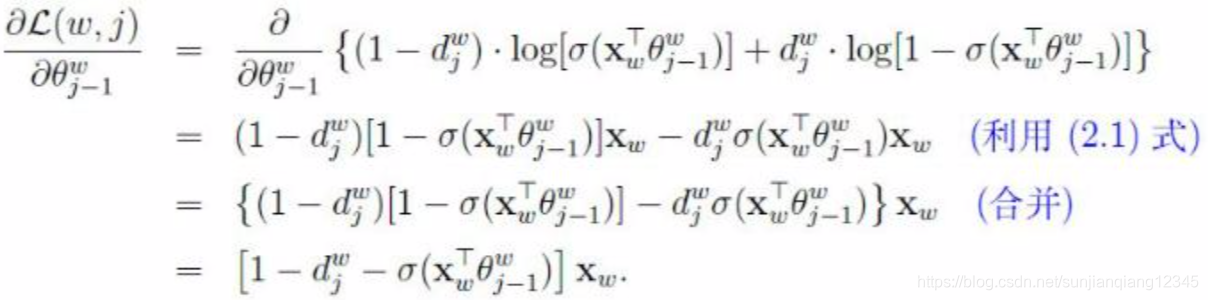
于是的更新公式为
![]()
中
和
是对称的,所以
![]()
表示
中各词词向量
的累加,
的更新公式为
![]()
③ 参数更新算法
设样本为,基于框架Hierarchical Softmax的CBOW的梯度上升法更新各参数的伪代码如下






 本文深入探讨了HierarchicalSoftmax技术在CBOW和Skip-gram模型中的应用,详细解析了这两种模型的网络结构、目标函数、条件概率计算方法以及参数更新算法。通过实例说明了如何利用Huffman树优化模型训练过程,提高效率。
本文深入探讨了HierarchicalSoftmax技术在CBOW和Skip-gram模型中的应用,详细解析了这两种模型的网络结构、目标函数、条件概率计算方法以及参数更新算法。通过实例说明了如何利用Huffman树优化模型训练过程,提高效率。
















 1551
1551

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








