本文是对《word2vec中的数学》(作者peghoty)的内容摘要。感谢作者,感谢为本文提供直接或间接帮助的人。
1、Huffman编码
(1)Huffman树
① 路径和路径长度
路径:在一棵树中,从一个结点往下可以到达的结点的通路;
路径长度:通路中分支的数目称为路径长度。例如,若规定根结点的层号为1,则从根结点到第L层的路径长度为L-1。
② 结点的权和带权路径长度
结点的权:为树中结点赋予一个具有某种含义的非负数值;
结点的带权路径长度:从根结点到该结点之间的“路径长度”与该结点的“权”的乘积。
③ 树的带权路径长度
树的带权路径长度:所有叶子结点的带权路径长度之和。
④ Huffman树
Huffman树:给定n个权重作为n个叶子结点的权重,构造一棵二叉树,若它的带权路径长度达到最小,则称这样的二叉树为Huffman树。
例:设“我”、“喜欢”、“观看”、“巴西”、“足球”、“世界杯”这6个词出现的次数分别是15、8、6、5、3、1。以这6个词为叶子结点,以相应的次品为权值,构造一棵Huffman树。
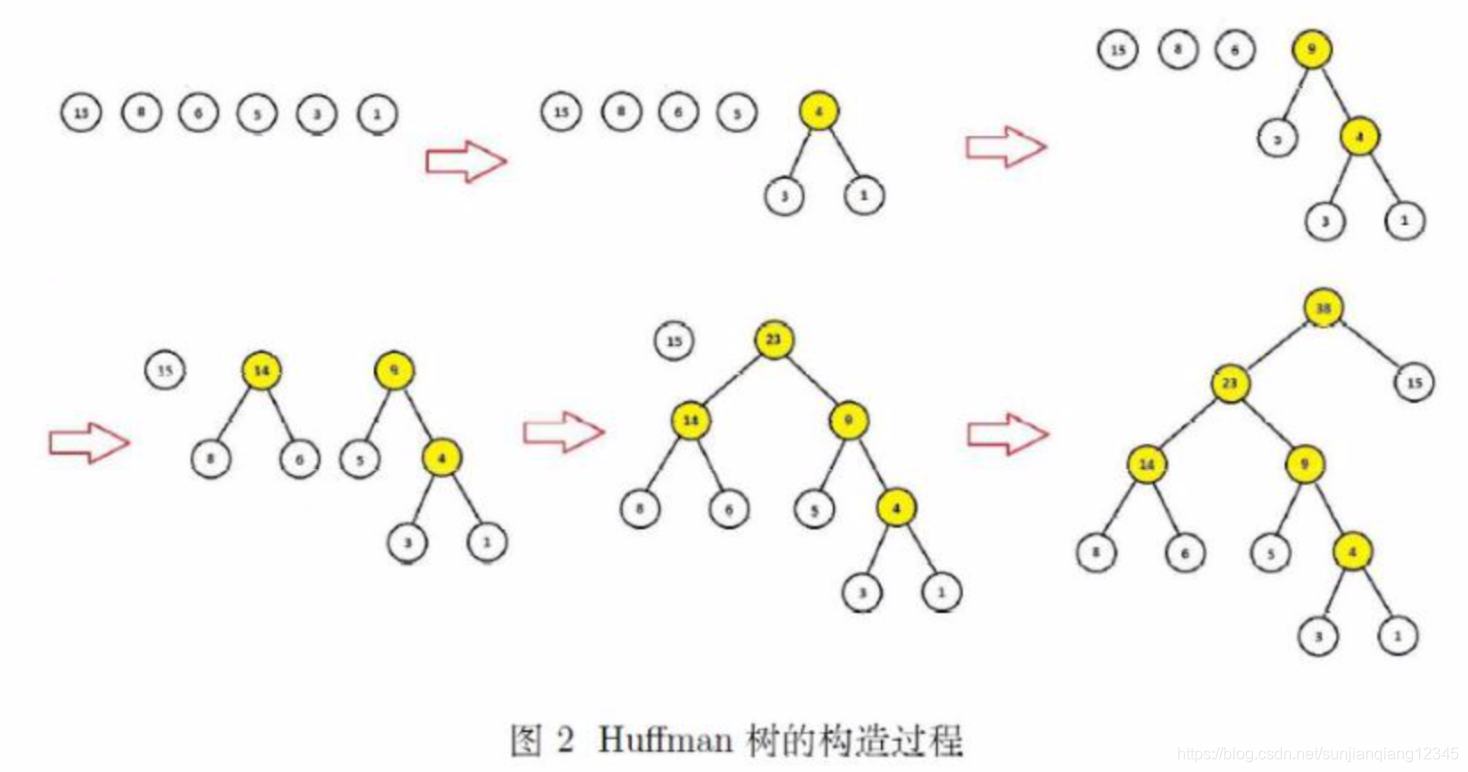
(2)Huffman树的构造
给定n个权重作为二叉树的n个叶子结点,可通过如下算法构造一棵Huffman树。
Huffman树构造算法:
① 将看成是有n棵树的森林(每棵树仅有一个结点)。
② 在森林中选出两个根结点的权重最小的树合并,作为一棵新树的左、右子树(一般将这两个根结点中权重大一点的作为左子树,权重小一点的作为右子树),且新树的根结点权重为其左、右子树根结点权值之和。
③ 从森林中删除选取的两棵树,并将新树加入森林。
④ 重复②、③步,直到森林中只剩一棵树为止,该树即为所求的Huffman树。
(3)构造Huffman树的数学原理 —— 排序不等式
排序不等式:设有两组数,和
,其中
,
,
为
的一个乱序排列,则有
,即
“逆序乘积之和”<=“乱序乘积之和”<=“顺序乘积之和”。
(4)Huffman编码
在数据通信中,需要将传输的文字转换成二进制的字符串,用0,1码的不同排列来表示字符。以字符出现的频次为权重,生成一棵Huffman树,在Huffman树中,将左子结点编码为1,右子结点编码为0,这样得到的叶结点的编码(即字符的编码)可以满足如下两个要求:
① 一个字符的编码不能是另一个字符编码的前缀;
② 传输报文的长度最短(根据排序不等式可知,“出现频次小的字符的编码长,而出现频次大的字符的编码短”)。
上例中得到的“我”、“喜欢”、“观看”、“巴西”、“足球”的Huffman编码为0, 111, 110, 101, 1001和1000。如下图所示:
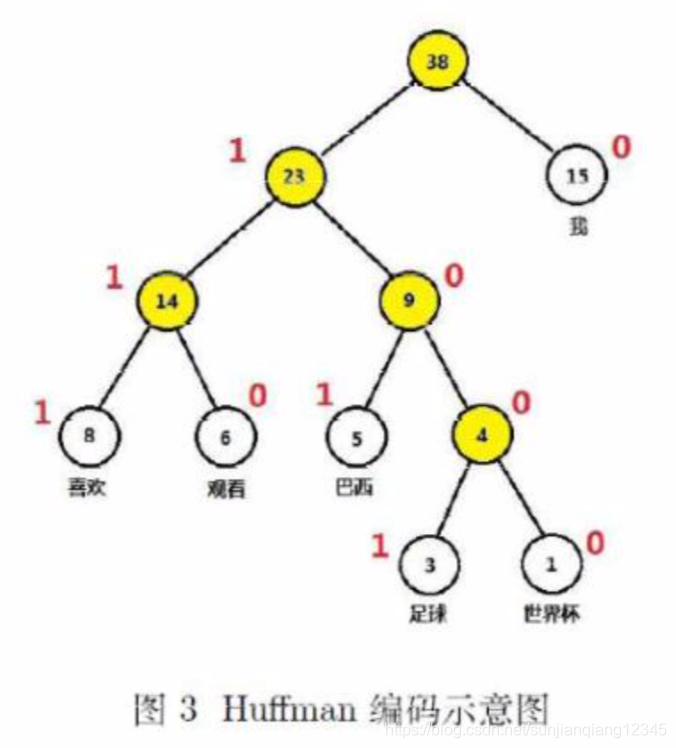





 本文介绍了Huffman编码的基本概念,包括Huffman树的构造原理和过程,以及如何利用Huffman树进行高效的数据压缩。通过具体实例展示了如何根据字符出现频率生成Huffman树,并为每个字符分配最优的二进制编码。
本文介绍了Huffman编码的基本概念,包括Huffman树的构造原理和过程,以及如何利用Huffman树进行高效的数据压缩。通过具体实例展示了如何根据字符出现频率生成Huffman树,并为每个字符分配最优的二进制编码。
















 4531
4531

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








