数据结构进阶(四)二叉排序树(二叉查找树)

注:构造一棵二叉排序树的目的，其实并不是为了排序(中序遍历)，而是为了提高查找、插入、删除关键字的速度。

定义

    二叉排序树又叫二叉查找树，英文名称是：Binary Sort Tree.BST的定义就不详细说了，我用一句话概括：左 < 中 < 右。 根据这个原理，我们可以推断：BST的中序遍历必定是严格递增的。

    二叉查找树是满足以下条件的二叉树：

    1.左子树上的所有节点值均小于根节点值；

    2.右子树上的所有节点值均不小于根节点值；

    3.左右子树也满足上述两个条件。

    二叉查找树是基于二叉树的，其结点数据结构定义为如下：

public class TreeNode {
  public Integer data;
    
  /*该节点的父节点*/ 
  public TreeNode parent;
    
  /*该节点的左子节点*/
  public TreeNode left;
    
  /*该节点的右子节点*/
  public TreeNode right;
    
  public TreeNode(Integer data) {
    this.data = data;
  }
  
  @Override
  public String toString() {
    return "TreeNode [data=" + data + "]";
  }
}

    现在明白了什么是二叉查找树，那么二叉查找树的基本操作又是如何来实现的呢？

查找

    在二叉查找树中查找x的过程如下：

    1、若二叉树是空树，则查找失败。

    2、若x等于根结点的数据，则查找成功，否则。

    3、若x小于根结点的数据，则递归查找其左子树，否则。

    4、递归查找其右子树。

   根据上述的步骤，写出其查找操作的代码：

  /**
   * @param data
   * @return TreeNode
   */
  public TreeNode findTreeNode(Integer data){
    if(null == root){
      return null;
    }
    TreeNode current = root;
    while(current != null){
      if(current.data > data){
        current = current.left;
      }else if(current.data < data){
        current = current.right;
      }else {
        return current;
      }
        
    }
    return null;
  }

插入

    二叉查找树的插入过程如下：

    1.若当前的二叉查找树为空，则插入的元素为根节点；

    2.若插入的元素值小于根节点值，则将元素插入到左子树中；

    3.若插入的元素值不小于根节点值，则将元素插入到右子树中。

  /**
   * 往树中加节点  
   * @param data
   * @return Boolean 插入成功返回true
   */
  public Boolean addTreeNode(Integer data) {
  
    if (null == root) {
      root = new TreeNode(data);
      System.out.println("数据成功插入到平衡二叉树中");
      return true;
    }
  
    TreeNode treeNode = new TreeNode(data);// 即将被插入的数据
    TreeNode currentNode = root;
    TreeNode parentNode;
  
    while (true) {
      parentNode = currentNode;// 保存父节点
      // 插入的数据比父节点小
      if (currentNode.data > data) {
        currentNode = currentNode.left;
        // 当前父节点的左子节点为空
        if (null == currentNode) {
          parentNode.left = treeNode;
          treeNode.parent = parentNode;
          System.out.println("数据成功插入到二叉查找树中");
          size++;
          return true;
        }
        // 插入的数据比父节点大
      } else if (currentNode.data < data) {
        currentNode = currentNode.right;
        // 当前父节点的右子节点为空
        if (null == currentNode) {
          parentNode.right = treeNode;
          treeNode.parent = parentNode;
          System.out.println("数据成功插入到二叉查找树中");
          size++;
          return true;
        }
      } else {
        System.out.println("输入数据与节点的数据相同");
        return false;
      }
    }     
}

删除

   二叉查找树的删除，分三种情况进行处理：

   1.p为叶子节点，直接删除该节点，再修改其父节点的指针（注意分是根节点和不是根节点），如图a。

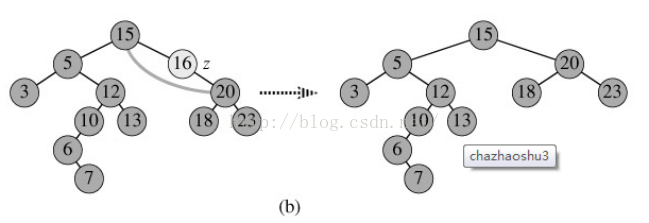
   2.p为单支节点（即只有左子树或右子树）。让p的子树与p的父亲节点相连，删除p即可；（注意分是根节点和不是根节点）；如图b。

   3.p的左子树和右子树均不空。找到p的后继y，因为y一定没有左子树，所以可以删除y，并让y的父亲节点成为y的右子树的父亲节点，并用y的值代替p的值；或者方法二是找到p的前驱x，x一定没有右子树，所以可以删除x，并让x的父亲节点成为y的左子树的父亲节点。如图c。

美文美图