支持向量机SVM

支持向量机

一.简介

  支持向量机（support vector machines）是一种二分类模型，它的目的是寻找一个超平面来对样本进行分割，分割的原则是间隔最大化，最终转化为一个凸二次规划问题来求解。由简至繁的模型包括：
当训练样本线性可分时，通过硬间隔最大化，学习一个线性可分支持向量机；
当训练样本近似线性可分时，通过软间隔最大化，学习一个线性支持向量机；
当训练样本线性不可分时，通过核技巧和软间隔最大化，学习一个非线性支持向量机；

二、线性可分支持向量机

   给定训练样本集$D=(x_1,y_1)，(x_2,y_2)，\cdots ,(x_m,y_m)$,其中yi∈{−1,+1}yi∈\{−1,+1\}yi∈{−1,+1},分类学习最基本的想法就是基于训练集$D$在样本空间中找到一个划分超平面，将不同类别的样本分开。

   直观看上去，能将训练样本分开的划分超平面有很多，但应该去找位于两类训练样本“正中间”的划分超平面，即图中红色的那条，因为该划分超平面对训练样本局部扰动的“容忍”性最好，例如，由于训练集的局限性或者噪声的因素，训练集外的样本可能比图中的训练样本更接近两个类的分隔界，这将使许多划分超平面出现错误。而红色超平面的影响最小，简言之，这个划分超平面所产生的结果是鲁棒性的。

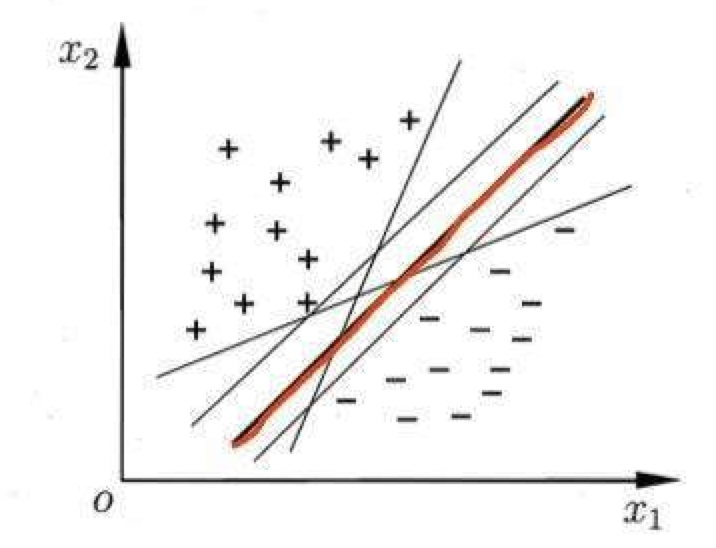
2.1. 那什么是线性可分呢？

​    如果一个线性函数能够将样本分开，称这些数据样本是线性可分的。那么什么是线性函数呢？其实很简单，在二维空间中就是一条直线，在三维空间中就是一个平面，以此类推，如果不考虑空间维数，这样的线性函数统称为超平面。我们看一个简单的二维空间的例子，$O$代表正类，$X$代表负类，样本是线性可分的，但是很显然不只有这一条直线可以将样本分开，而是有无数条，我们所说的线性可分支持向量机就对应着能将数据正确划分并且间隔最大的直线。

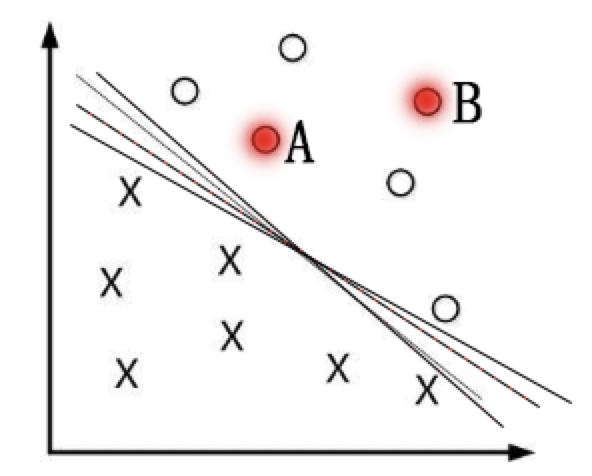
   那么我们考虑第一个问题，为什么要间隔最大呢？一般来说，一个点距离分离超平面的远近可以表示分类预测的确信度，如图中的A B两个样本点，B点被预测为正类的确信度要大于A点，所以SVM的目标是寻找一个超平面，使得离超平面较近的异类点之间能有更大的间隔，即不必考虑所有样本点，只需让求得的超平面使得离它近的点间隔最大。
   接下来考虑第二个问题，怎么计算间隔？只有计算出了间隔，才能使得间隔最大化。

任意点$\vec{x}$到超平面$w^T+b=0$的距离：$r=\frac{{\vec{w}}^T\vec{x}}{||w||}$
对任意$\forall$正样本$(\overrightarrow{x_i},y_i)\in D$,有
${\vec{w}}^T{x}_i>c$时，$y_i=1$
${\vec{w}}^T{x}_i>c<=>{\vec{w}}^T{x}_i+b>0<=>{\vec{w}}^T{x}_i+b>1$(因为$b$是常数，为了计算方便写成1)
同理对任意$\forall$负样本$(\overrightarrow{x_i},y_i)\in D$,有${\vec{w}}^T{x}_i+b<-1$时，$y_i=-1$
$$f(x)=\{\begin{array}{ll}{\vec{w}}^T{x}_i+b\ge 1& y_i=+1\\ {\vec{w}}^T{x}_i+b\le -1& y_i=-1\end{array}$$
即：$y_i({\vec{w}}^T{x}_i+b)\ge 1$
其中$\vec{w}$为法向量，决定了超平面的方向，$b$为位移量，决定了超平面与原点的距离。​ 该公式被称为最大间隔假设，$y_i=+1$ 表示样本为正样本，$y_i=-1$ 表示样本为负样本。
距离超平面${\vec{w}}^T{x}_i+b=0$最近的几个点使上式等号成立，他们被称为”支持向量“。虚线称为边界，两条虚线间的距离称为间隔（margin）。

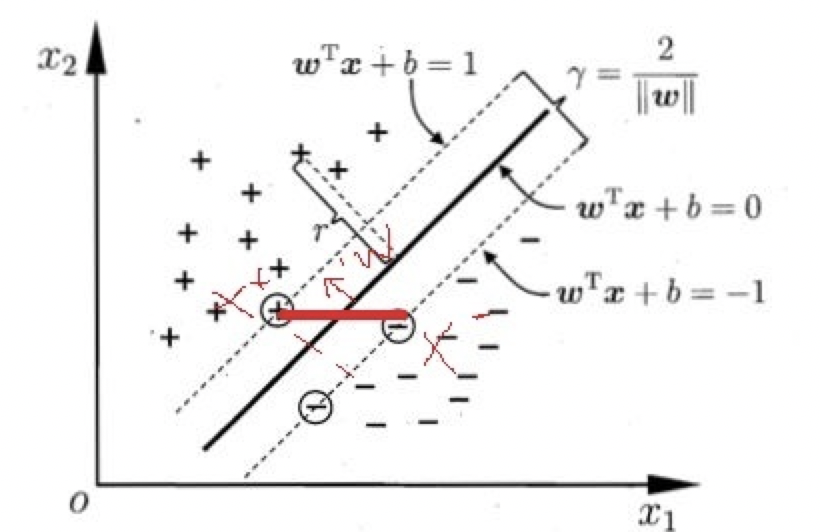
两条平行线间的距离公式：$\frac{1-b-(-1-b)}{||w||}=\frac{2}{||w||}$
两类样本距离最大的因素仅仅和最佳超平面的法向量有关。
至此，我们求得了间隔，SVM的思想是使得间隔最大化，即：
$$\{\begin{array}{l}\max \frac{2}{||w||}\\ st.y_i({\vec{w}}^T{x}_i+b)\ge 1,i=1,2,...,n\end{array}（2.1）$$

显然，最大化 $\frac{2}{||w||}$相当于最小化 $||w||$，为了计算方便，将公式转化成如下公式:
$$\{\begin{array}{l}\min \frac{1}{2}||w|{|}^2\\ st.y_i({\vec{w}}^T{x}_i+b)\ge 1,i=1,2,...,n\end{array}（2.2）$$
等价于：
$$\{\begin{array}{l}\min \frac{1}{2}||w|{|}^2\\ st.1-y_i({\vec{w}}^T{x}_i+b)\le 0,i=1,2,...,n\end{array}（2.3）$$
该基本型是一个凸二次规划问题，可以采用拉格朗日乘子法对其对偶问题求解，拉格朗日函数：
$$L(\vec{w},b,\vec{\alpha })=\frac{1}{2}||w|{|}^2-\sum _{i=1}^n{\alpha }_i(y_i({\vec{w}}^T{x}_i+b)-1),其中\alpha >0（2.4）$$
对$w,b$求导后：
$$\{\begin{array}{l}\vec{w}={\sum }_{i=1}^n{\alpha }_i{y}_i\overrightarrow{x_i}\\ {\sum }_{i=1}^n{\alpha }_i{y}_i=0\end{array}（2.5）$$
将上式带入拉格朗日函数中得到：
$$\{\begin{array}{l}L(\vec{w},b,\vec{\alpha })={\sum }_{i=1}^n{\alpha }_i-\frac{1}{2}{\sum }_{i=1}^n{\sum }_{1=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j\overrightarrow{x_i}\overrightarrow{x_j}\\ {\sum }_{i=1}^n{\alpha }_i{y}_i=0\\ {\alpha }_i\ge 0,i=1,2,...,n\end{array}（2.6）$$
原问题就转换为如下关于$\alpha$ 的问题：

$$\{\begin{array}{l}max{\sum }_{i=1}^n{\alpha }_i-\frac{1}{2}{\sum }_{i=1}^n{\sum }_{1=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j\overrightarrow{x_i}\overrightarrow{x_j}\\ st.{\sum }_{i=1}^n{\alpha }_i{y}_i=0\\ {\alpha }_i\ge 0,i=1,2,...,n\end{array}（2.7）$$
由上可知，不关心单个样本如何，只关心样本件两两的成积。
求解出$\overrightarrow{{\alpha }_i}$之后，再求解$\vec{w}$和$b$即可得到SVM模型。
$$f(\vec{x})=\vec{w}\vec{x}+b=\sum _{1=1}{\alpha }_i{y}_i{\overrightarrow{x_i}}^T\overrightarrow{x_i}+b（2.8）$$

2.2.SVM的KKT条件

$$\{\begin{array}{l}minf(x)\\ st.h_j(x)=0,j=1,2...,p\\ g_k(x)\le 0,k=1,2,...,q\end{array}（2.9）$$

等价于：
$$\{\begin{array}{l}L(\vec{w},b,\vec{\alpha })对x求导为零\\ h(x)=0\\ ag(x)=0,a\ge 0\end{array}（2.10）$$
对应的SVM的KKT条件：
$$\{\begin{array}{l}{\alpha }_i\ge 0\\ y_i(w_i^T\vec{x}+b)-1\ge 0,i=1,2,...,n\\ {\alpha }_i{y}_i(w_i^T\vec{x}+b-1）=0\end{array}（2.11）$$
我们分析一下，对于任意的训练样本 $(x_i,y_i)$，
若 ${\alpha }_i=0$，则其不会在公式（2.8）中的求和项中出现，也就是说，它不影响模型的训练；
若 ${\alpha }_i>0$，则$y_{i}f(x_i)-1=0$，也就是 $y_{i}f(x_i)=1$，即该样本一定在边界上，是一个支持向量。
这里显示出了支持向量机的重要特征：当训练完成后，大部分样本都不需要保留，最终模型只与支持向量有关。

三、非线性支持向量机和核函数

对于非线性问题，线性可分支持向量机并不能有效解决，要使用非线性模型才能很好地分类。先看一个例子，如下图，很显然使用直线并不能将两类样本分开，但是可以使用一条椭圆曲线（非线性模型）将它们分开。非线性问题往往不好求解，所以希望能用解线性分类问题的方法求解，因此可以采用非线性变换，将非线性问题变换成线性问题。

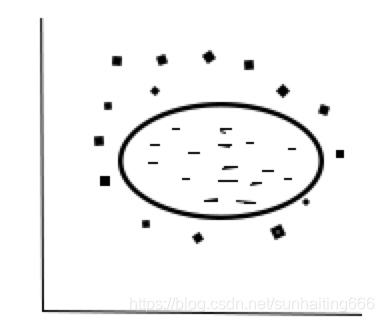
对于这样的问题，可以将训练样本从原始空间映射到一个更高维的空间，使得样本在这个空间中线性可分，如果原始空间维数是有限的，即属性是有限的，那么一定存在一个高维特征空间是样本可分。令ϕ(x)表示将 x 映射后的特征向量，于是在特征空间中，划分超平面所对应的的模型可表示为：
$$f(x)={\vec{w}}^T\varphi (x)+b(3.1)$$
于是有最小化函数：
$$\{\begin{array}{l}\min \frac{1}{2}||w|{|}^2\\ st.1-y_i({\vec{w}}^T\varphi (x_i)+b)\le 0,i=1,2,...,n\end{array}（3.2）$$
其对偶问题为：
$$\{\begin{array}{l}max{\sum }_{i=1}^n{\alpha }_i-\frac{1}{2}{\sum }_{i=1}^n{\sum }_{1=1}{\alpha }_i{\alpha }_j{y}_i{y}_j\varphi (x_i{)}^T\varphi (x_j)\\ st.{\sum }_{i=1}^N{\alpha }_i{y}_i=0\\ {\alpha }_i\ge 0,i=1,2,...,n\end{array}（3.3）$$

若要对公式（3.3）求解，会涉及到计算 $\varphi (x_i{)}^T\varphi (y_i)$，这是样本 $x_i$ 和 $x_j$ 映射到特征空间之后的内积，由于特征空间的维数可能很高，甚至是无穷维，因此直接计算 $\varphi (x_i{)}^T\varphi (y_i)$通常是困难的，于是想到这样一个函数：

$$\kappa (x_i,x_j)=<\varphi (x_i),\varphi (x_j)>=\varphi (x_i{)}^T\varphi (x_j)(3.4)$$
即 $x_i$ 和 $x_j$ 在特征空间中的内积等于他们在原始样本空间中通过函数$\kappa (x_i,x_j)$计算的函数值，于是公式（3.3）写成如下：
$$\{\begin{array}{l}max{\sum }_{i=1}^n{\alpha }_i-\frac{1}{2}{\sum }_{i=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j\kappa (x_i,x_j)\\ st.{\sum }_{i=1}^N{\alpha }_i{y}_i=0\\ {\alpha }_i\ge 0,i=1,2,...,n\end{array}（3.3）$$
求解后得到：
$$\begin{array}{rl}f(x)& =w^T\varphi (x)+b\\ & =\sum _{i=1}^n{\alpha }_i{y}_i\varphi (x_i{)}^T\varphi (x_j)+b\\ & =\sum _{i=1}^n{\alpha }_i{y}_i\kappa (x_i,x_j)+b\end{array}(3.4)$$
这里的函数$\kappa (x_i,x_j)$ 就是核函数，在实际应用中，通常人们会从一些常用的核函数里选择（根据样本数据的不同，选择不同的参数，实际上就得到了不同的核函数），下面给出常用的核函数：

• 线性核：

$$\kappa (x_i,x_j)=x_i^T{x}_j$$

• 多项式核（d是多项式的次数，d=1是退化为线性核）：
  $$\kappa (x_i,x_j)=(x_i^T{x}_j{)}^d$$

• 高斯核（$\sigma >0$）：
  $$\kappa (x_i,x_j)=exp(\frac{||x_i-x_j|{|}^2}{2{\sigma }^2})$$

• 拉普拉斯核（$\sigma >0$）：
  $$\kappa (x_i,x_j)=exp(\frac{||x_i-x_j||}{\sigma })$$

• sigmiod核（$\beta >0,\theta <0$）：
  $$\kappa (x_i,x_j)=tanh(\beta x_i^T{x}_j+\theta )$$

此外，核函数也可以通过组合得到，在此不再赘述。

四、线性支持向量机（软间隔支持向量机）与松弛变量

4.1、线性支持向量机

  在前面的讨论中，我们假设训练样本在样本空间或者特征空间中是线性可分的，但在现实任务中往往很难确定合适的核函数使训练集在特征空间中线性可分，退一步说，即使瞧好找到了这样的核函数使得样本在特征空间中线性可分，也很难判断是不是由于过拟合造成。
  线性不可分意味着某些样本点 $(x_i,y_i)$不能满足间隔大于等于1的条件，样本点落在超平面与边界之间。为解决这一问题，可以对每个样本点引入一个松弛变量 ${\xi }_i\ge 0$，使得间隔加上松弛变量大于等于1，这样约束条件变为：
$$y_i(w^T{x}_i+b)\ge 1-{\xi }_i(4.1)$$

同时，对于每一个松弛变量 ${\xi }_i\ge 0$，支付一个代价 ${\xi }_i\ge 0$，目标函数变为

$$\frac{1}{2}||w|{|}^2+C\sum _{i=1}^m{\xi }_i(4.2)$$

其中 $C>0$为惩罚参数，$C$值大时对误分类的惩罚增大， $C$值小时对误分类的惩罚减小，公式（4.2）包含两层含义：使 $\frac{1}{2}||w|{|}^2$尽量小即间隔尽量大，同时使误分类点的个数尽量小，$C$是调和两者的系数。
有了公式（4.2），可以和线性可分支持向量机一样考虑线性支持向量机的学习过程，此时，线性支持向量机的学习问题变成如下凸二次规划问题的求解（原始问题）：
$$\{\begin{array}{l}\min \frac{1}{2}||w|{|}^2+C{\sum }_{i=1}^m{\xi }_i\\ st.y_i(w^T{x}_i+b)\ge 1-{\xi }_i,i=1,2,...,n\end{array}（4.3）$$
2、对偶问题
与线性可分支持向量机的对偶问题解法一致，公式（4.3）的拉格朗日函数为：
$$L(w,b,\alpha ,\xi ,\mu )=\frac{1}{2}||w|{|}^2+C\sum _{i=1}^m{\xi }_i+\sum _{i=1}^n{\alpha }_i(1-{\xi }_i-y_i(w^T{x}_i+b))-\sum _{i=1}^n{\mu }_i{\xi }_i(4.4)$$
其中${\alpha }_i>0,{\mu }_i\ge 0$是拉格朗日乘子。
令$L(w,b,\alpha ,\xi ,\mu )$对$w,b,\xi$的偏导数为0可得如下：
$$\{\begin{array}{l}w={\sum }_{i=1}^n{\alpha }_i{y}_i{x}_i\\ {\sum }_{i=1}^n{\alpha }_i{y}_i=0\\ C={\alpha }_i+{\mu }_i\end{array}（4.5）$$
将公式(4.5)代入公式（4.4）得对偶问题：
$$\{\begin{array}{l}max{\sum }_{i=1}^n{\alpha }_i-\frac{1}{2}{\sum }_{i=1}^n{\sum }_{1=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j\overrightarrow{x_i}\overrightarrow{x_j}\\ st.{\sum }_{i=1}^n{\alpha }_i{y}_i=0{\alpha }_i\ge 0,{\mu }_i\ge 0,C={\alpha }_i+{\mu }_i,i=1,2,...,n\end{array}（4.6）$$

解出 $\alpha$ 之后，根据公式(4.5)可以求得 $w$ ， 进而求得 $b$，可以得到模型：

$$f(\vec{x})=w^{T}x+b=\sum _{1=1}{\alpha }_i{y}_i{x}_i^T{x}_i+b（4.7）$$

上述过程的KKT条件为：
$$\{\begin{array}{l}{\alpha }_i\ge 0\\ y_{i}f(x_i)\ge 1-{\xi }_i\\ {\alpha }_i(y_{i}f(x_i)-1+{\xi }_i)=0\\ {\xi }_i>0,{\mu }_i{\xi }_i=0\end{array}（4.8）$$
我们分析一下，对于任意的训练样本 $(x_i,y_i)$，总有 ${\alpha }_i=0$或者$y_{i}f(x_i)-1+{\xi }_i=0$，若 ${\alpha }_i=0$，则其不会在公式（2.8）中的求和项中出现，也就是说，它不影响模型的训练；
若 ${\alpha }_i>0$，必有$y_{i}f(x_i)-1+{\xi }_i=0$，也就是 $y_{i}f(x_i)=1-{\xi }_i$，此时该样本是一个支持向量，由于$C={\alpha }_i+{\mu }_i$；
若 ${\alpha }_i<C$，则必有${\mu }_i>0$，根据公式（4.8）知 ${\xi }_i=0$，即该样本恰好落在最大间隔的边界上；
若 ${\alpha }_i=C$，则${\mu }_i=0$，此时若 ${\xi }_i\le 1$，则该样本在最大间隔的内部；若${\xi }_i>1$则样本分类错误。

五、总结

  至此，关于SVM的三类问题：线性可分支持向量机与硬间隔最大化，非线性支持向量机与核函数，线性支持向量机与软间隔最大化一一介绍完毕。
  我们所面对的所有的机器学算法，都是有适用范围的，或者说，我们所有的机器学习算法都是有约束的优化问题。而这些约束，就是我们在推导算法之前所做的假设。
  比如：Logistics Regression，在Logistics Regression中，假设后验概率为Logistics 分布；再比如：LDA假设fk(x)是均值不同，方差相同的高斯分布；这些都是我们在推导算法之前所做的假设，也就是算法对数据分布的要求。
  而对于SVM而言，它并没有对原始数据的分布做任何的假设，这就是SVM和LDA、Logistics Regression区别最大的地方。这表明SVM模型对数据分布的要求低，那么其适用性自然就会更广一些。如果我们事先对数据的分布没有任何的先验信息，即，不知道是什么分布，那么SVM无疑是比较好的选择。
  但是，如果我们已经知道数据满足或者近似满足高斯分布，那么选择LDA得到的结果就会更准确。如果我们已经知道数据满足或者近似满足Logistics 分布，那么选择Logistics Regression就会有更好的效果。

六、python代码实现

from sklearn import svm
import matplotlib.pyplot as plt
import numpy as np

x = [[1, 8], [3, 20], [1, 15], [3, 35], [5, 35], [4, 40], [7, 80], [6, 49]]
y = [1, 1, -1, -1, 1, -1, -1, 1]
# 线性核函数（linear），多项式核函数（poly），高斯核函数（rbf），拉普拉斯核函数（laplace）和Sigmoid核函数
"""
    核函数(这里简单介绍了sklearn中svm的四个核函数，还有precomputed及自定义的)
        
    LinearSVC：主要用于线性可分的情形。参数少，速度快，对于一般数据，分类效果已经很理想
    RBF:主要用于线性不可分的情形。参数多，分类结果非常依赖于参数
    polynomial:多项式函数,degree 表示多项式的程度-----支持非线性分类
    Sigmoid：在生物学中常见的S型的函数，也称为S型生长曲线

    说明2：根据设置的参数不同，得出的分类结果及显示结果也会不同
"""
clf = svm.SVC()  # 默认参数：kernel='rbf'
# clf = svm.LinearSVC() # 其不支持kernel参数，因为设计思想就是线性分类。如果确定数据, 可以进行线性划分，可以选择此函数
clf.fit(x, y)
# 预测
result = clf.predict([[2, 2]])  # 两个方括号表示传入的参数是矩阵而不是list
print("预测结果：", result)

print(np.array(x).reshape(1, -1))
# 根据训练出的模型绘制样本点
for i in x:
    # 我们不知道z的shape属性是多少，
    # #但是想让z变成只有一行，列数不知道多少，
    # #通过`z.reshape(1,-1)`，Numpy自动计算出有16行，
    # 新的数组shape属性为(16, 1)，与原来的(2, 8)配套。
    print("====", np.array(i).reshape(1, -1))
    res = clf.predict(np.array(i).reshape(1, -1))
    if res > 0:
        plt.scatter(i[0], i[1], c='r', marker='*')
    else:
        plt.scatter(i[0], i[1], c='g', marker='*')
# 生成随机实验数据(15行2列)
rdm_arr = np.random.randint(1, 15, size=(15, 2))
# 回执实验数据点
for i in rdm_arr:
    res = clf.predict(np.array(i).reshape(1, -1))
    if res > 0:
        plt.scatter(i[0], i[1], c='r', marker='.')
    else:
        plt.scatter(i[0], i[1], c='g', marker='.')
# 显示绘图结果
plt.show()