递归
1.什么是递归?
函数自己调用自己的情况
c语言 + 数据结构 (二叉、快排、归并)
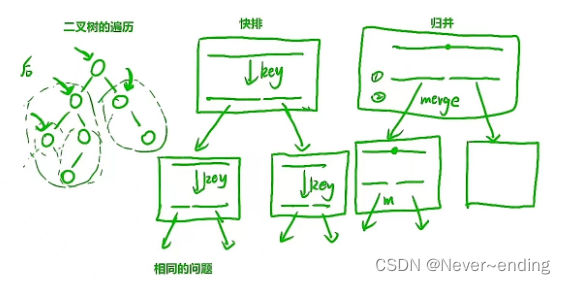
二叉树的后序遍历:
从根节点开始,先进左子树,再进右子树,到左子树之后重复这个过程,返回之后进右子树重复这个过程,最后遍历根节点。
快速排序:
找到基准元素之后先向左边排序,再向右边排序,进入左边之后重复这个过程,返回之后进右边重复这个过程,最终整合。
归并排序:
将一个待排序段分成两份,左边进行归并,右边进行归并,最终整体归并。
2.为什么会用到递归?
本质:
主问题 -> 相同的子问题
子问题 -> 相同的子问题
..................................
3.如何理解递归?(分成三个层次)
1.递归展开的细节图
2.二叉树中的题目
3.宏观看待递归的过程
1.不要在意递归的细节展开图 2.把递归的函数当成一个黑盒
3.相信这个黑盒一定能完成这个任务
//伪代码,二叉树后序遍历
void dfs(TreeNode* root)
{
//细节-出口
if(root == nullptr)
return;
else
{
dfs(root->left);
dfs(root->right);
printf(root->val);
}
}
//伪代码,归并
void merge(nums, int left, int right)
{
//细节-出口
if(left >= right)
return;
int mid = (left + right) / 2;
merge(nums, left, mid);
merge(nums, mid + 1 right);
//合并两个有序数组
}
4.如何写好一个递归?
1.先找到相同的子问题!!! -> 函数头的设计
2.只关心某一个子问题是如何解决的 -> 函数体的书写
3.注意一下递归函数的出口即可
搜索 vs 深度优先遍历 vs 深度优先搜索 vs 宽度优先遍历 vs 宽度优先搜索 vs 暴搜
1.对比
深度优先遍历 vs 深度优先搜索(DFS)
宽度优先遍历 vs 宽度优先搜索(BFS)
=====》本质上是一致的
遍历是形式,目的是搜索
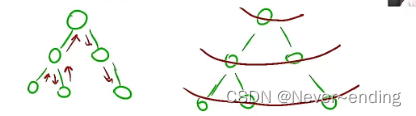
2.关系图
暴力枚举一遍所有的情况
搜索(暴搜)=DFS+BFS
3.拓展搜索问题
全排列问题(树状图结构问题都可以)
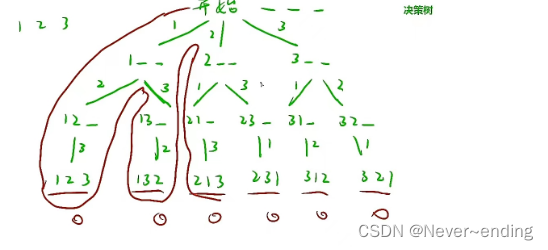
三、回溯与剪枝
回溯本质就是深搜,就是深搜过程中做了错误的决定,调回到分支处(红色线就相当于回溯)
剪枝就是回到多分支处发现原本其中一条路走过了,不再走了,相当于把它去掉了
四、整合以及规划
专题一:递归
专题二:二叉树中的深搜
专题三: 穷举vs暴搜vs深搜vs回湖vs剪枝
专题四:综合练习
专题五: FloodFill 算法
专题六:记忆化搜索




 本文介绍了递归的基本概念、在数据结构(如二叉树后序遍历、快速排序和归并排序)中的应用,探讨了递归的本质和理解方法,比较了深度优先遍历与宽度优先遍历,以及回溯和剪枝技巧。最后概述了相关专题的学习路径。
本文介绍了递归的基本概念、在数据结构(如二叉树后序遍历、快速排序和归并排序)中的应用,探讨了递归的本质和理解方法,比较了深度优先遍历与宽度优先遍历,以及回溯和剪枝技巧。最后概述了相关专题的学习路径。
















 4479
4479










