ML/DL学习笔记2——偏差和方差模型好坏

    不同的model对应的error是不同的那么error是怎么来的呢？这里引入偏差和方差这两个概念。

概念引入

 偏差（bias）：描述的是预测值（估计值）的期望与真实值之间的差距。偏差越大，越偏离真实数据。
 方差（variance）：描述的是预测值的变化范围，离散程度，也就是离其期望值的距离。方差越大，数据的分布越分散。

  红色靶心表示为实际值，蓝色点集为预测值。

  低偏差，低方差：这是训练的理想模型，此时蓝色点集基本落在靶心范围内，且数据离散程度小，基本在靶心范围内。
  低偏差，高方差：这是深度学习面临的最大问题，过拟合了。也就是模型太贴合训练数据了，导致其泛化（或通用）能力差，若遇到测试集，则准确度下降的厉害。
  高偏差，低方差：这往往是训练的初始阶段。
  高偏差，高方差：这是训练最糟糕的情况，准确度差，数据的离散程度也差。

                                             李宏毅DL笔记P4

抽样分布

 $\hat{y}$ 和 $y\ast$真值和估测值
 $\hat{y}$ 表示那个真正的function，而$f\ast$表示这个$\hat{f}$ 的估测值
就好像在打靶，$\hat{f}$是靶的中心点，收集到一些data做training以后，你会得到一个你觉得最好的function即$f\ast$，这个$f\ast$落在靶上的某个位置，它跟靶中心有一段距离，这段距离就是由Bias和variance决定的。bias表示所有$f\ast$的平均落靶位置和真值靶心的距离，variance表示这些$f\ast$的集中程度

 抽样分布的理论(概率论与数理统计)
 假设独立变量为x(这里的x代表每次独立地从不同的training data里训练找到的$f\ast$)，那么：

  总体方差是一组资料中各数值与其算术平均数离差平方和的平均数。

 用样本均值$\overline{x}$ 估测总体期望u

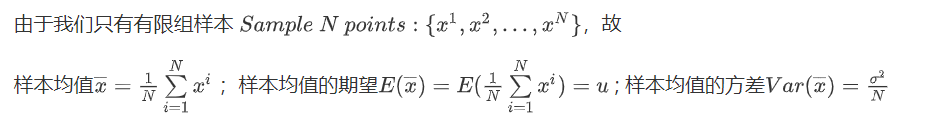
     补充数学知识：算术平均是来自样本的，是近似的；数学期望是母体的，是精确的。

 样本均值 $\overline{x}$ 的期望是总体期望u也就是说是按概率对称地分布在总体期望u的两侧的；而 $\overline{x}$ 分布的密集程度取决于N，即数据量的大小，如果N比较大， $\overline{x}$ 就会比较集中，如果N比较小， $\overline{x}$ 就会以为中心分散开来。综上，样本均值$\overline{x}$