python算法题——搜索篇 poj2488

骑士之旅

描述

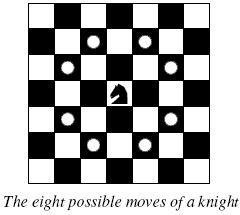
背景 骑士厌倦了一次又一次地看到相同的黑白方块，并决定环游世界。每当骑士移动时，它在一个方向上是两个正方形，一个垂直于这个方向的正方形。骑士的世界是他赖以生存的棋盘。我们的骑士生活在一个棋盘上，棋盘的面积比普通的 8 * 8 棋盘小，但它仍然是矩形的。你能帮助这位冒险的骑士制定旅行计划吗？

问题 找到一条路径，让骑士访问每个方块一次。骑士可以在棋盘的任何方块上开始和结束。

输入

输入以第一行的正整数 n 开头。以下行包含 n 个测试用例。

每个测试用例由一行组成，其中包含两个正整数 p 和 q，使得 1 <= p * q <= 26。

这表示一个 p * q 棋盘，其中 p 描述有多少个不同的平方数 1， . . . ， p 存在，q 描述存在多少个不同的方格字母。

这些是拉丁字母表的第一个q字母：A。

输出

每个方案的输出都以包含"Scenario #i:"的行开头，其中 i 是从 1 开始的方案编号。

然后打印一行，其中包含按字典顺序排列的第一条路径，该路径访问棋盘的所有方块，骑士移动后跟一条空线。

路径应通过连接所访问的方块的名称在一行上给出。每个方格名称由一个大写字母后跟一个数字组成。 如果不存在这样的路径，则应在一行上输出不可能。

示例输入

3
1 1
2 3
4 3

示例输出

Scenario #1:
A1
​
Scenario #2:
impossible
​
Scenario #3:
A1B3C1A2B4C2A3B1C3A4B2C4

大致题意，给定一个棋盘的大小，骑士从任意点出发，访问棋盘上每一个点一次，有无这种可能

这题只是需要输出方法和可能性，那么可以用DFS，但是开始点是不确定的，所以有可能需要换开始点

但是这有一个显而易见的问题，从四个角落开始的话就是端点，端点的好处就是只能向外出，而除端点外的点开始的话。。。好吧，也不是不可能

打表

dx = [1, 1, -1, -1, 2, 2, -2, -2]
dy = [2, -2, 2, -2, 1, -1, 1, -1]

DFS

def DFS(x, y, a, b, t):
    if t >= a * b:
        print("路径是：")
    for i in range(8):
        xx = x + dx[i]
        yy = y + dy[i]
        if temp[xx][yy]:
            continue
        temp[xx][yy] = True
        DFS(xx, yy, a, b, t + 1)
        temp[xx][yy] = False

既然DFS需要传递这么多参数，再加上需要输出路径，为何不定义一个结构体呢？

结构体

class node:
    def __init__(self, x, y, t, action, points):
        self.x = x
        self.y = y
        self.t = t
        self.action = action
        self.points = points

DFS2.0

def DFS2(f):
    if f.t >= a * b:
        print(len(f.action))
        print(f.action)
        exit(0)
        #如果需要将所有方案输出可以用
        #return
    for i in range(8):
        xx = f.x + dx[i]
        yy = f.y + dy[i]
        if xx >= a or yy >= b:
            continue
        if xx < 0 or yy < 0:
            continue
        if temp[xx][yy]:
            continue
        temp[xx][yy] = True
        newnode = node(xx, yy, f.t + 1, [], [])
        newnode.action = copy.deepcopy(f.action)
        newnode.action.append(i)
        newnode.points = copy.deepcopy(f.points)
        newnode.points.append([xx + 1, yy + 1])
        DFS2(newnode)
        temp[xx][yy] = False

main

if __name__ == '__main__':
    a, b = map(int, input().split())
    
    for i in range(a):
        for j in range(b):
            #每次调用DFS前都需要将棋盘初始化
            #1.初始化temp记录有无走过
            temp = [[False for i in range(b)]for i in range(a)]
            temp[i][j] = True
            #DFS(i, j, a, b, 1)
            node1 = node(i, j, 1, [0], [[i + 1, j + 1]])
            DFS2(node1)

因为a, b是定义在main中的变量，在其他函数中可以访问到！

用deepcopy记得import copy

完整代码

import copy
​
​
class node:
    def __init__(self, x, y, t, action, points):
        self.x = x
        self.y = y
        self.t = t
        self.action = action
        self.points = points
​
def DFS2(f):
    if f.t >= a * b:
        print(len(f.action))
        print(f.action)
        print(f.points)
        exit(0)
        #return
    for i in range(8):
        xx = f.x + dx[i]
        yy = f.y + dy[i]
        if xx >= a or yy >= b:
            continue
        if xx < 0 or yy < 0:
            continue
        if temp[xx][yy]:
            continue
        temp[xx][yy] = True
        newnode = node(xx, yy, f.t + 1, [], [])
        newnode.action = copy.deepcopy(f.action)
        newnode.action.append(i)
        newnode.points = copy.deepcopy(f.points)
        newnode.points.append([xx + 1, yy + 1])
        DFS2(newnode)
        temp[xx][yy] = False
​
if __name__ == '__main__':
    a, b = map(int, input().split())
​
    dx = [1, 1, -1, -1, 2, 2, -2, -2]
    dy = [2, -2, 2, -2, 1, -1, 1, -1]
​
    for i in range(a):
        for j in range(b):
            # 每次调用DFS前都需要将棋盘初始化
            # 1.初始化temp记录有无走过
            temp = [[False for i in range(b) ]for i in range(a)]
            temp[i][j] = True
            # DFS(i, j, a, b, 1)
            node1 = node(i, j, 1, [0], [[i + 1, j + 1]])
            DFS2(node1)

此代码输出

4 3 #输入

12 #步数

[0, 4, 6, 1, 4, 6, 1, 0, 7, 5, 2, 7] #每次的方案

[[1, 1], [3, 2], [1, 3], [2, 1], [4, 2], [2, 3], [3, 1], [4, 3], [2, 2], [4, 1], [3, 3], [1, 2]] #每次的地方