12.快速排序

快排的思想：如果要排序数组中下标从 p 到 r 之间的一组数据，我们选择 p 到 r 之间的任意一个数据作为 pivot（分区点）。

  我们遍历 p 到 r 之间的数据，将小于 pivot 的放到左边，将大于 pivot 的放到右边，将 pivot放到中间。经过这一步骤之后，数组 p 到 r 之间的数据就被分成了三个部分，前面 p 到 q-1之间都是小于 pivot 的，中间是 pivot，后面的 q+1 到 r 之间是大于 pivot 的。

  根据分治、递归的处理思想，我们可以用递归排序下标从 p 到 q-1 之间的数据和下标从 q+1 到r 之间的数据，直到区间缩小为 1，就说明所有的数据都有序了。

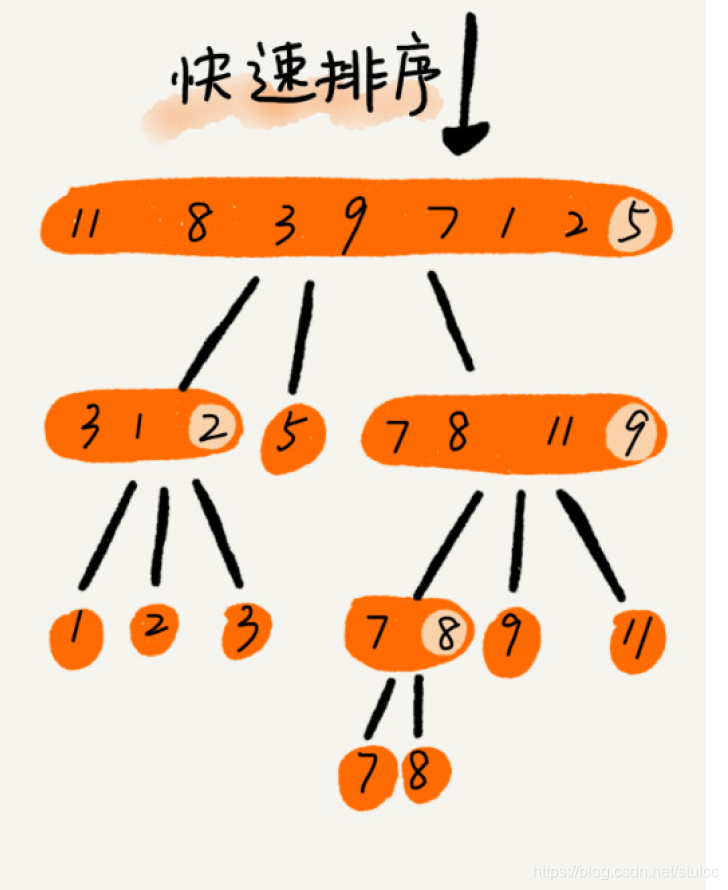
如果我们用递推公式来将上面的过程写出来的话，就是这样：

递推公式：
quick_sort(p…r) = quick_sort(p…q-1) + quick_sort(q+1, r)
终止条件：
p >= r

• 快速排序也可以很快解决top k问题
• 和归并排序相比解决了空间复杂度的问题，原地排序
• 是不稳定排序，原因是因为分区的过程涉及交换操作，i所在的位置第一个不符合标准的元素，后面接着还有不符合标准的元素，当我们再往后发现了j是符合标准的元素，此时就要交换i和j位置。此时原先在前的元素就跑到后面了。所以说是不稳定排序算法。
• 时间复杂度是O(nlogn)，极端情况下可能退化成O(n)。

public class SortQuick {

    public static void main(String[] args) {
        int a[] = {9, 8, 5, 6, 3, 4, 1, 2};
        new SortQuick().quicksort(a, 0, a.length - 1);
        for (int i = 0; i < a.length; i++) {
            System.out.print(a[i] + ", ");
        }
        System.out.println();
        new SortQuick().selectTopK(a, 3);
        for (int i = 0; i < 3; i++) {
            System.out.print(a[i] + ", ");
        }
    }

    public void selectTopK(int[] nums, int k) {
        int partition = partition(nums, 0, nums.length - 1);
        while (partition != k) {
            if (partition > k) {
                //说明还需要进一步缩小空间获取前k大
                partition = partition(nums, 0, partition - 1);
            } else {
                //说明还需要扩大空间获取前k大
                partition = partition(nums, partition + 1, nums.length - 1);
            }
        }
    }

    /**
     * 这里是递归，递归都要使用递归公式来思考代码的编写
     *
     * @param nums
     * @param start
     * @param end
     */
    public void quicksort(int[] nums, int start, int end) {
        if (start >= end) {
            return;
        }
        int partition = partition(nums, start, end);
        quicksort(nums, start, partition - 1);
        quicksort(nums, partition + 1, end);
    }

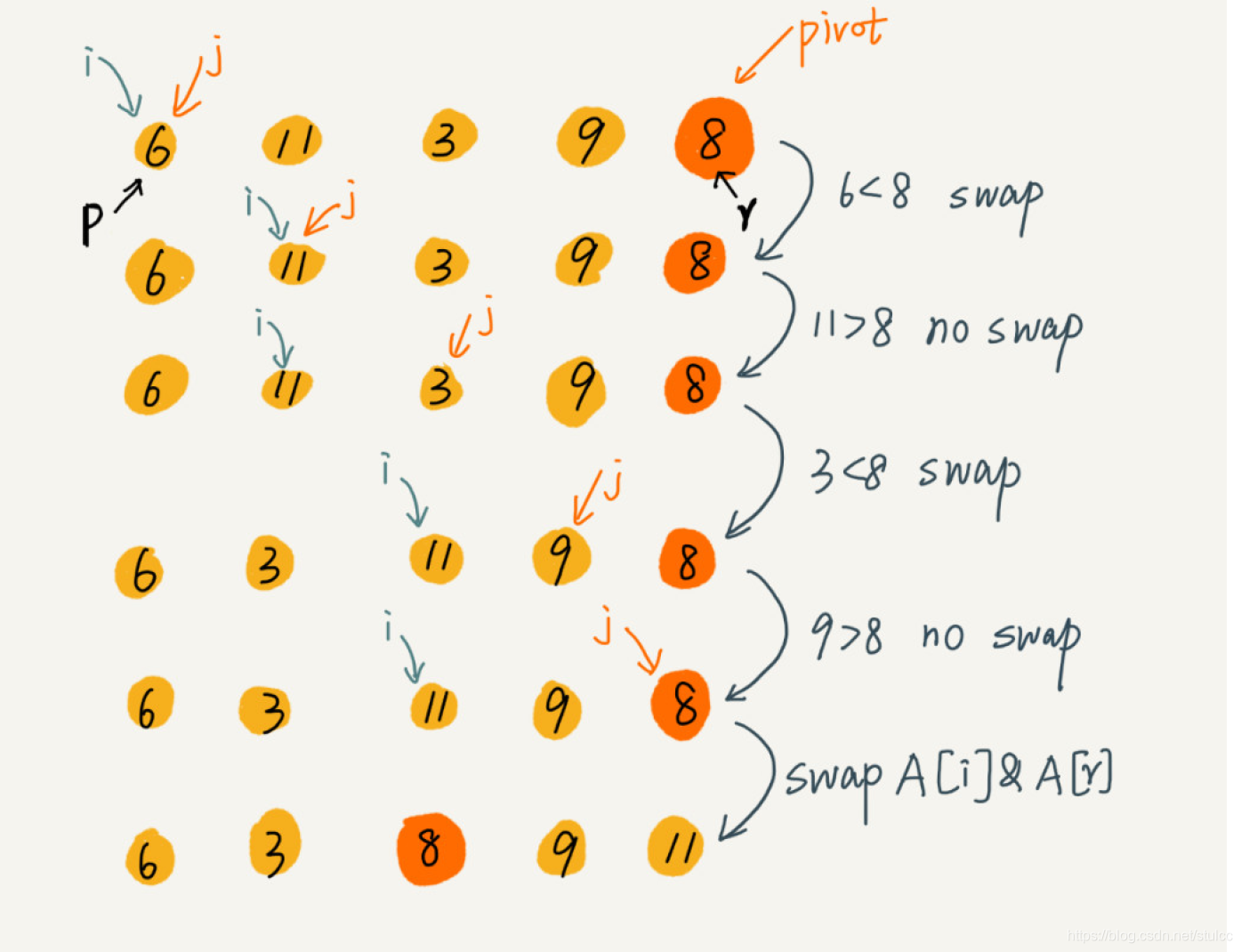
    public int partition(int[] nums, int start, int end) {
        //选取最后一个作为基点，比他小的放前面，比他大的放后面
        int point = end;
        int index = start;//从start到index的值比较小的
        for (int i = start; i <= end; i++) {
            if (nums[i] < nums[point]) {
                //如果当前i是满足条件的，就把它放到index上
                int temp = nums[index];
                nums[index] = nums[i];
                nums[i] = temp;
                index++;
            }
        }
        //把基准数挪到角标这里
        int temp = nums[index];
        nums[index] = nums[point];
        nums[point] = temp;
        return index;
    }
}