文章提供了一种使用自定义的平衡二叉搜索树（SBT）解决数组中子数组累加和在特定范围内的数量问题。通过维护SBT的平衡，以及重写添加和查询方法，可以高效地计算出符合条件的子数组个数。此外，文章还提到了归并排序的解决方案作为对比。
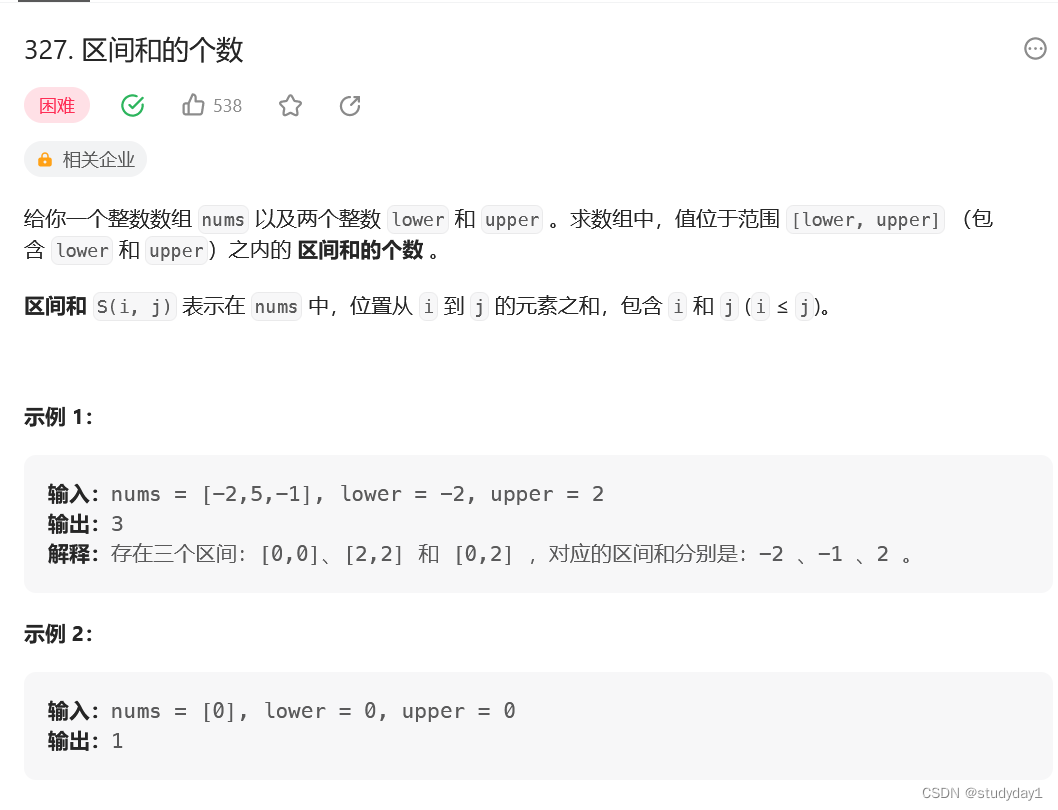
一、题目一
给定一个数组arr，和两个整数a和b（a<=b）求arr中有多少个子数组，累加和在[a,b]这个范围上返回达标的子数组数量
class Solution {
//自定义SBT节点类
public static class SBTNode {
public long key; //节点key值 因为题目是一个一维数组 不需要设定value
public SBTNode l; //节点左子节点
public SBTNode r; //节点右子节点
public long size; //节点作为头节点的子树的节点个数
public long all; //辅助变量：目标数组添加一个数则累计加1 包括有重复数字的 ，添加重复Key值的 SB树是覆盖 而不会新增
public SBTNode(long k) { //构造函数 初始化值
key = k;
size = 1;
all = 1;
}
}
//自定义SBT树类
public static class SizeBalancedTreeSet {
private SBTNode root; //SBT树的根节点 头节点
private HashSet<Long> set = new HashSet<>(); //集合 存放元素 利用其唯一性可以判断下个加入节点是否重复 注意要实例化对象避免空指针异常
//右旋操作
private SBTNode rightRotate(SBTNode cur) {
//求出数组的重复数值 就是cur当前节点的all 减去左右子树的all 剩下的就是cur当前节点的重复个数
long same = cur.all - (cur.l != null ? cur.l.all : 0) - (cur.r != null ? cur.r.all : 0);
//操作右旋 就是cur下来右节点 其左节点上到cur位置
SBTNode left = cur.l; //左子节点提出
cur.l = left.r; //cur当前节点的左树 赋值 左子节点的右子树
left.r = cur; //左子节点的右子树 赋值 当前节点
left.size = cur.size; //左子节点上移到cur位置 更新节点的个数
cur.size = (cur.l != null ? cur.l.size : 0) + (cur.r != null ? cur.r.size : 0) + 1;
left.all = cur.all; //左子节点上移到cur位置 更新节点的all数组元素添加个数 包含重复数值
cur.all = (cur.l != null ? cur.l.all : 0) + (cur.r != null ? cur.r.all : 0) + same; //cur刷新all 就需要添加当前的左右子树all值 以及 在之前cur位置时的保存的重复数值个数same
return left;
}
//左旋操作
private SBTNode leftRotate(SBTNode cur) {
//求出数组的重复数值 就是cur当前节点的all 减去左右子树的all 剩下的就是cur当前节点的重复个数
long same = cur.all - (cur.l != null ? cur.l.all : 0) - (cur.r != null ? cur.r.all : 0);
//操作左旋 就是cur下来左节点 其右节点上到cur位置
SBTNode right = cur.r; //右子节点提出
cur.r = right.l; //cur当前节点的右树 赋值 左子节点的左子树
right.l = cur; //左右子节点的左子树 赋值 当前节点
right.size = cur.size; //右子节点上移到cur位置 更新节点的个数
cur.size = (cur.l != null ? cur.l.size : 0) + (cur.r != null ? cur.r.size : 0) + 1;
right.all = cur.all; //右子节点上移到cur位置 更新节点的all数组元素添加个数 包含重复数值
cur.all = (cur.l != null ? cur.l.all : 0) + (cur.r != null ? cur.r.all : 0) + same; //cur刷新all 就需要添加当前的左右子树all值 以及 在之前cur位置时的保存的重复数值个数same
return right;
}
//SBT树，调整平衡方法 返回调整后的新头节点
// 注意这里的平衡 是根据 叔叔节点数 大于 全部每个侄子节点数 否则就是不平衡要调整
//与AVL树相同分四种情况 LL LR RR RL
//每一种对应的调整平衡旋转都一样 右旋 ； 对子节点左旋再对当前节点右旋 ； 左旋； 对子节点右旋再对当前节点左旋
//不一样的地方在于 SBT树还需要再判断那些节点的孩子节点变化了 对这些节点 要递归继续调整平衡，因为可能会调整了树位置后 又多出了一些不平衡的情况
// LL 调整后 cur.r cur两个节点的孩子节点发生变化 所以就对两个节点递归进行再次调整
// LR cur.l cur.r cur 三个节点
// RR cur.l cur 两个节点
// RL cur.l cur.r cur 三个节点
private SBTNode maintain(SBTNode cur) {
if (cur == null) return null; //cur空树 直接返回null
//根据平衡特性 叔叔节点与侄子节点的比较 分别取出 cur.l cur.l.l cur.l.r ; cur.r cur.r.l cur.r.r 六个节点进行比较
//也就是cur的左右子树 以及孙子树
long leftSize = cur.l != null ? cur.l.size : 0;
long leftLeftSize = cur.l != null && cur.l.l != null ? cur.l.l.size : 0;
long leftRightSize = cur.l != null && cur.l.r != null ? cur.l.r.size : 0;
long rightSize = cur.r != null ? cur.r.size : 0;
long rightLeftSize = cur.r != null && cur.r.l != null ? cur.r.l.size : 0;
long rightRightSize = cur.r != null && cur.r.r != null ? cur.r.r.size : 0;
if (leftLeftSize > rightSize) { //1.左左侄子树 大于 右叔叔树 LL型
cur = rightRotate(cur); //当前节点右旋
cur.r = maintain(cur.r); //当前节点的右子节点 其孩子节点变化 需要递归调用再调整看看是否不平衡了
cur = maintain(cur); //等右子节点调整好 再调整cur节点 因为其孩子节点肯定也是变化了
} else if (leftRightSize > rightSize) { //2. 左右侄子树 大于 右叔叔树 LR型
cur.l = leftRotate(cur.l); //当前节点的左子节点 左旋
cur = rightRotate(cur); //当前节点 右旋 把孙子节点提上来
cur.l = maintain(cur.l); //当前节点的左子节点 其孩子节点变化 需要递归调用再调整看看是否不平衡了
cur.r = maintain(cur.r); //当前节点的右子节点 其孩子节点变化 需要递归调用再调整看看是否不平衡了
cur = maintain(cur); //等左右子节点调整好 再调整cur节点 因为其孩子节点肯定也是变化了
} else if (rightRightSize > leftSize) { //3.右右侄子树 大于 左叔叔树 RR型
cur = leftRotate(cur); //当前节点左旋
cur.l = maintain(cur.l); //当前节点的左子节点 其孩子节点变化 需要递归调用再调整看看是否不平衡了
cur = maintain(cur); //等左子节点调整好 再调整cur节点 因为其孩子节点肯定也是变化了
} else if (rightLeftSize > leftSize) { //4. 右左侄子树 大于 左叔叔树 RL型
cur.r = rightRotate(cur.r); //当前节点的右子节点 右旋
cur = leftRotate(cur); //当前节点 左旋 把孙子节点提上来
cur.l = maintain(cur.l); //当前节点的左子节点 其孩子节点变化 需要递归调用再调整看看是否不平衡了
cur.r = maintain(cur.r); //当前节点的右子节点 其孩子节点变化 需要递归调用再调整看看是否不平衡了
cur = maintain(cur); //等左右子节点调整好 再调整cur节点 因为其孩子节点肯定也是变化了
}
return cur; //最后要返回刷新的当前新头节点
}
//添加指定key值到SBT树中,返回新根节点 当前根节点cur 添加key值 当前SBT树是否存在key值节点
private SBTNode add(SBTNode cur, long key, boolean falg) {
if (cur == null) {
return new SBTNode(key); //SBT树空，直接实例化新节点返回
} else {
//树非空 那么就添加到树中 首先all就要加1 进来一个树 all就+1
cur.all++;
if (key == cur.key) {
return cur; //递归树直到cur相等时 就返回当前节点给上层
} else { //如果没有遇到，那么就会继续左右下沉
if (!falg) { //如果树是不包含该节点的
//如果当前key 不包含 那么size就要加1
cur.size++;
}
if (key < cur.key) {
//如果key 小于当前节点 那么就节点左下移动 节点值减小
cur.l = add(cur.l, key, falg);
} else {
//否则就是 大于当前节点 等于的已经在前面判断了 节点右下移动 节点值扩大
cur.r = add(cur.r, key, falg);
}
return maintain(cur); //最后添加完 需要往上每个节点进行平衡调整
}
}
}
//外部接口： 给树添加指定值
public void add(long sum) {
boolean falg = set.contains(sum); //判断集合中是否已经有相同值节点
root = add(root, sum, falg); //从根节点开始的整个SBT树 添加sum值 返回新根节点刷新
set.add(sum); //最后需要把该值加入集合中 用来判断重复值
}
//外部接口： 返回小于key的有多少个节点
public long lessKeySize(long key) {
SBTNode cur = root; //cur作为 SBT树的根节点 用于待会的树遍历
long ans = 0; //ans用于接收 小于key的节点树
while (cur != null) {
//遍历整个树 直到下层节点为空
//如果当前节点等于key 那么 小于key的 就是当前ans的累加值 以及其左子树的all值 表示有多少节点数经过 直接返回
if (cur.key == key) {
return ans + (cur.l != null ? cur.l.all : 0);
} else if (cur.key > key) {
//如果当前值大于key 那么需要继续往左子树下层 找到小于key的节点
cur = cur.l;
} else {
//如果当前值小于key 说明其左子树以及当前值 都是小于key的 那么就存在符合情况 将当前数的all 减去右子树all 剩下的就左子树和当前节点的all 这些就是符合条件的 进行累加
ans += cur.all - (cur.r != null ? cur.r.all : 0);
cur = cur.r; //然后cur当前节点继续往右看看有没有还小于key的
}
}
return ans; //最后返回ans的结果值
}
//外部接口： 返回大于key的有多少个节点
//反过来就是需要求出 小于等于key的有多少个节点 然后再将头节点的all减去 小于key的我们有方法（key） 那么小于等于key 不就是 （key+1)
public long moreKeySize(long key){
return root != null ? (root.all - lessKeySize(key+1)) : 0;
}
}
/**
* 主方法
* 给定一个数组arr，和两个整数a和b（a<=b）
* 求arr中有多少个子数组，累加和在[a,b]这个范围上
* 返回达标的子数组数量
*/
public static int countRangeSum(int[] nums, int lower, int upper){
//定义自定义SBT树类结构对象 支持添加入数字 这里我们添加的是前缀和数值 可以接收重复的数值，SBT树中本身不存在重复值，我们通过改写添加all属性进行数值个数累加
SizeBalancedTreeSet treeSet = new SizeBalancedTreeSet();
//前缀和
long sum = 0;
//结果子数组个数
int ans = 0;
//一开始 没有前缀 先给SBT树加一个 0 的前缀和
treeSet.add(0);
for(int i = 0; i < nums.length; i++){
sum += nums[i]; //前缀和累加
//求 多少个子数组 累加和在[lower,upper]范围上
//转换成有多少个 每次遍历数组i位置时 0开始的前缀和 右区间范围0,i-1索引 前缀和在 [sum - upper, sum - lower]范围的有多少个
//假设我们的前缀区间是[10,20] 那么我们调用树结构的接口方法 只有小于key的方法 可以这样转换：
// F(10) 表示 >10 F(21) 表示 >21 F(21) - F(10) 就表示 [10,20]的范围了
long a = treeSet.lessKeySize(sum - lower + 1);
long b = treeSet.lessKeySize(sum - upper);
ans += a- b; //ans进行累加 区间就是 a-b 就是前缀和在 [sum - upper, sum - lower]范围的个数 也就是表示i结尾的子数组有多少个累加和在[lower,upper]范围内
treeSet.add(sum); //然后要把sum前缀和 加入SBT树结构中 如果有存在同样前缀和的 SBT树会进行处理 也就是重复的值会一起计算
}
return ans; //最后返回结果
}
//方法二： 改写归并排序
// public static int countRangeSum(int[] nums, int lower, int upper) {
// if(nums == null || nums.length == 0) return 0;
// //根据题意，将数组转换成一个前缀和数组，即i位置值为0-i区间数据元素的和,注意要用long类型，累加防止整数溢出
// long[] sum = new long[nums.length];
// sum[0] = nums[0]; //先赋值第一个，第一个前缀和就是只有自己
// for(int i = 1;i<sum.length;i++){
// sum[i] = nums[i] + sum[i-1];
// }
// //归并排序传入的是前缀和数组，用来处理题意要求的区间
// return process(sum,0,sum.length-1,lower,upper);
// }
// public static int process(long[] arr,int l ,int r,int lower,int upper){
// //base case:左右索引相等，指向前缀和数组中同一个值，因为合并函数是严格确保了左右数组都有，所以这种特例会漏了
// // 需要单独处理。那么就表示，从0-l个元素区间的和，判断是否在区间内，在则返回1，递归中进行累加
// if(l == r){
// return arr[l] >= lower && arr[l] <= upper ? 1 :0;
// }
// int m = l + ((r-l)>>1);
// return process(arr,l,m,lower,upper) +
// process(arr,m+1,r,lower,upper)+
// merge(arr,l,m,r,lower,upper);
// }
// public static int merge(long[] arr,int l, int m, int r,int lower,int upper){
// //题意是找区间值符合[lower,upper]，那么意思就是在每个元素i往左的全部组合区间是否存在[lower,upper]，可以
// //转换成i元素之前的不包括i,的前缀和中，有多少个前缀和在[arr[i]-upper,arr[i]-lower]，
// //这样处理就能一次循环中得到右数组元素为结尾的在左数组区间，一共有多少个符合的前缀和。
// //合并前先判断 右数组[m+1,r]中从左往右每一个元素i，在左数组[l,m]中依次遍历匹配是否在左数组中存在有
// // [[arr[i]-upper,arr[i]-lower]的前缀和 有则获取
// int ans = 0;
// //区间是在左数组中找的 所以范围在l,m之间
// int windowL = l;
// int windowR = l;
// //外层遍历每个右数组元素
// for(int i = m+1;i<=r;i++){
// //根据前面提到的转换逻辑，定义出左数组的左右边界范围
// long max = arr[i] - lower;
// long min = arr[i] - upper;
// //内层遍历左数组的元素所以左右指针都是不超过m
// //这里遍历左指针是小于min 右指针是大于等于max 所以右指针跳出时是会多出一个不符合的值的，就是左闭右开
// while(windowR<=m && arr[windowR]<=max){
// windowR++;
// }
// while(windowL<=m && arr[windowL]<min){
// windowL++;
// }
// //遍历完之后就开始累计左右指针包含了多少个区间符合的 [windowL,windowR)
// ans += windowR - windowL;
// }
// //下面就是合并逻辑
// long[] help = new long[r-l+1];
// int index = 0;
// int p1 = l;
// int p2 = m+1;
// while(p1<=m&&p2<=r){
// help[index++] = arr[p1]<=arr[p2]? arr[p1++]:arr[p2++];
// }
// while(p1<=m){
// help[index++] = arr[p1++];
// }
// while(p2<=r){
// help[index++] = arr[p2++];
// }
// for(int i =0;i<help.length;i++){
// arr[l+i] = help[i];
// }
// return ans;
// }
}
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
