数据结构：三元组的构建、相加和快速转置

最新推荐文章于 2025-09-29 15:43:20 发布

原创

最新推荐文章于 2025-09-29 15:43:20 发布 · 1.1w 阅读

133 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c语言 #数据结构

本文介绍稀疏矩阵的三元组表存储方法，包括三元组表的定义、构建过程、相加操作及快速转置算法，并提供详细的代码实现。

1.三元组表的定义

三元组研究目的对于在实际问题中出现的大型的稀疏矩阵，若用常规分配方法在计算机中储存，将会产生大量的内存浪费，而且在访问和操作的时候也会造成大量时间上的浪费，为了解决这一问题，从而产生了多种解决方案。由于其自身的稀疏特性，通过压缩可以大大节省稀疏矩阵的内存代价。

主要是用来存储稀疏矩阵的一种压缩方式，也叫三元组表。假设以顺序存储结构来表示三元组表（triple table），则得到稀疏矩阵的一种压缩存储方式，即三元组顺序表，简称三元组表。

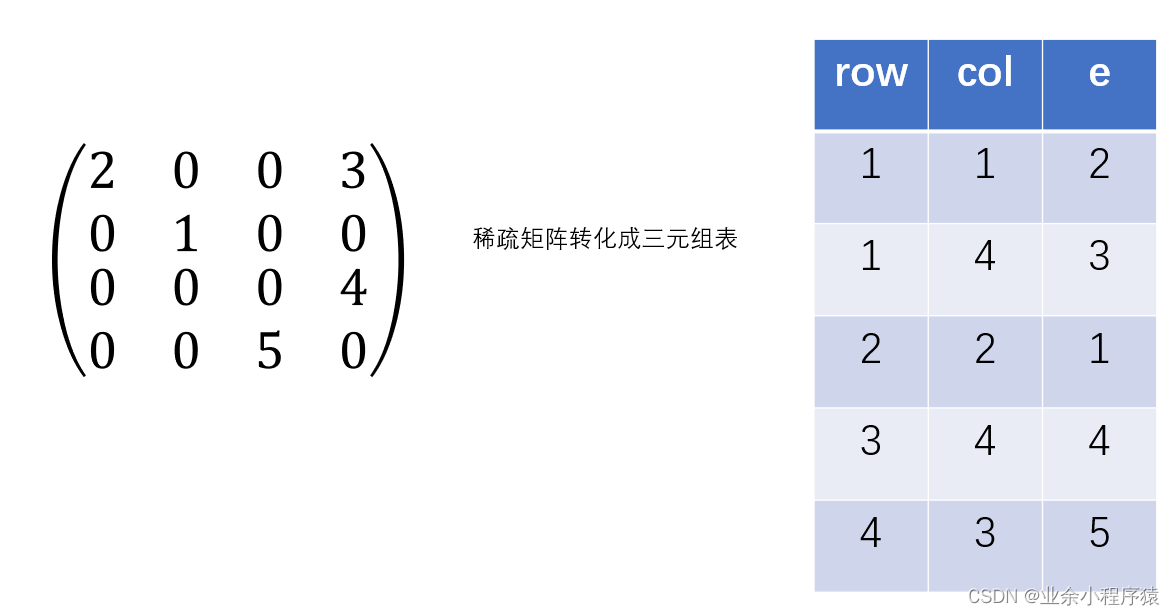
2.三元组表的数据结构

#define MAX 1000

typedef struct
{
	int row,col,e;    //数据所在的行、列，数值
}Triple;

typedef struct
{
	Triple  data[MAX+1];
	int mu,nu,tu;		//矩阵的行数，列数和非零元个数
}TSMatrix;

3.三元组表的构建

思路：从第一行开始遍历查找非零元素，存入三元组表data[tu]中，data[tu].row=i，data[tu].col=j，data[tu].e=a[i][j]

void input(TSMatrix *p,int m,int n)
{
	int i,j;
	int a[100][100];
	for( i=1;i<=m;i++)    //随机生成稀疏矩阵
	for(j=1;j<=n;j++)
	{
		if(1+rand()%4>=1+rand()%19)
			a[i][j]=1+rand()%99;
		else
			a[i][j]=0;
	}
	for(int i=1;i<=m;i++){    //打印出该稀疏矩阵
	for(int j=1;j<=n;j++)
	{

		printf("%4d",a[i][j]);
	}printf("\n");
	}
	p->tu=0;    //三元组表的总个数
	for(i=1;i<=m;i++)    //进行查找非零元素进行存储
	for(j=1;j<=n;j++)
	{
		if(a[i][j]!=0)
		{
		p->data[p->tu].row=i;	//行
		p->data[p->tu].col=j;	//列
		p->data[p->tu].e=a[i][j];	//	数据
		++p->tu;
		}
	}

}

4.输出三元组表

void printTriple(TSMatrix *p)
{
	printf("\n三元组：\n");
	for(int i=0;i<p->tu;i++)
	{
		printf("%4d %4d %4d\n",p->data[i].row,p->data[i].col,p->data[i].e);
	}
}