搞懂Halcon的弧形角度和与X轴角度

原创已于 2024-05-06 10:15:59 修改 · 1.3k 阅读

5 ·

CC 4.0 BY-SA版权

文章标签：

#开发语言 #c++

于 2024-04-30 00:38:05 首次发布

一. 搞懂定义

1.Halcon 弧形

关键参数是起始角度和终点角度范围可选(0~6.28) 或者是（0~-6.28），还有就是方向order： positive是逆时针转， negative是顺时针。

2.直线与X轴夹角

定义：绕着起始点转到 x轴的角度（x轴可由起始点及其右边的点构成），范围包括 0~3.14 -3.14~0。

二. 直线和X轴夹角代码测试

观察直线与轴夹角，可以用以下代码

dev_close_window ()
dev_open_window (0, 0, 512, 512, 'white', WindowID)
RowA1 := 255
ColumnA1 := 10

RowA2 := 255
ColumnA2 := 501

dev_set_color ('red')

disp_line (WindowID, RowA1, ColumnA1, RowA2, ColumnA2)
dev_set_color ('black')

AngleTuple:=[]
RadTuple:=[]
RowB1 := 255
ColumnB1 := 255
for i := 1 to 360 by 5    //角度转为弧度
    RowB2 := 255 + sin(rad(i)) * 200       
    ColumnB2 := 255 + cos(rad(i)) * 200   //x是cos   y是sin
    disp_line (WindowID, RowB1, ColumnB1, RowB2, ColumnB2)
    angle_lx (RowB1, ColumnB1, RowB2, ColumnB2, Angle)
    RadTuple:=[RadTuple,rad(i)]
    AngleTuple:=[AngleTuple,Angle]

endfor

效果如下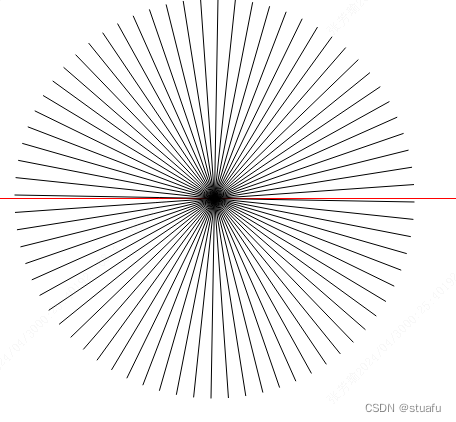

范围就是 0~3.14 -3.14~0 （3.14 也是-3.14）

三.弧线的起始点和终止点

那么如果在halcon 已知一段圆弧（通过拟合轮廓得出，可以获取起始角度终止角度方向，但是正角度可能正负都有），需要遍历起始角度和终点角度求出圆弧上的每个点坐标（步）。这里不用轮廓提取点的方法。需要注意的是弧线的角度，和通过三角函数求点的角度不是同一概念，先通过以下代码获取得到首尾点，下图较大的红十字。

startAng:=360- (start_angle_rad)/3.14159*180
endAng:= 360-(end_angle_rad)/3.14159*180

RowB2 := 255 + sin(2*3.14159-start_angle_rad) * radius       
ColumnB2 := 255 + cos(2*3.14159-start_angle_rad) * radius   //x是cos   y是sin
gen_cross_contour_xld(Cross, RowB2, ColumnB2, 20, 0)

RowB3 := 255 + sin(2*3.14159-end_angle_rad) * radius       
ColumnB3:= 255 + cos(2*3.14159-end_angle_rad) * radius   //x是cos   y是sin
gen_cross_contour_xld(Cross2, RowB3, ColumnB3, 40, 0)

四.通过角度遍历弧线每一点

继续考虑角度的各种情况，处理思路
1.先将弧度转为0~6.24之间
2.再针对顺逆方向，起始终止谁大谁小，进行调整角度。


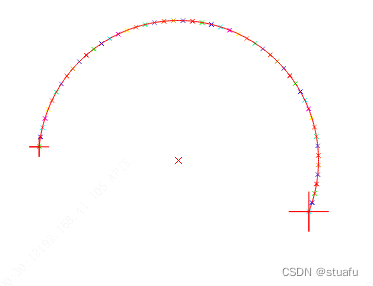
* 定义圆心坐标和半径
row_center := 255
col_center := 255
radius := 100
num_points:=50
start_angle_rad := -4.56851606560302
end_angle_rad :=6.755260182603
order:='negative'


* 初始化轮廓对象用于显示点
gen_empty_obj(ArcPoints)

if( start_angle_rad<0 )
    start_angle_rad:=start_angle_rad+6.28
endif

if( end_angle_rad<0 )
    end_angle_rad:=end_angle_rad+6.28
endif





**以下代码可封装为GenCrossCircleRad (SinPoints, ArcPoints, ContCircle1, start_angle_rad, end_angle_rad, row_center, col_center, radius, num_points, order, angleTupleSin, angleTuple)
**



gen_circle_contour_xld(ContCircle, row_center, col_center, radius, start_angle_rad,end_angle_rad,order, 1)


gen_cross_contour_xld(Point, row_center, col_center, 10, 0.785)  // 注意坐标顺序，先y后x
concat_obj(ArcPoints, Point, ArcPoints)



if(order=='positive')
    if(start_angle_rad>end_angle_rad)
       
        end_angle_rad:=end_angle_rad+6.28
    endif    
endif



if(order=='negative' )
    if(start_angle_rad<end_angle_rad)
       
        start_angle_rad:=start_angle_rad+6.28
    endif    
endif





*如果是角度  那么化简到 -PI~PI  然后逐步添加角度差
*

angle_step_rad := (end_angle_rad - start_angle_rad) / num_points


angleTupleSin:=[]

* 遍历角度
for i := 0 to num_points by 1
    angle_rad := start_angle_rad + i * angle_step_rad 
    
    *x := col_center + radius * sin(angle_rad)  // 使用cos计算X坐标
    *y := row_center + radius * cos(angle_rad)  // 使用sin计算Y坐标
    
     y := 255 - sin(angle_rad) * radius       
     x := 255 + cos(angle_rad) * radius   //x是cos   y是sin
     
   
    angleTupleSin:=[angleTupleSin,angle_rad]
    * 生成点，并添加到轮廓对象
     gen_cross_contour_xld(Point, y, x, 6+i*0.0, 0.785)  // 注意坐标顺序，先y后x
    concat_obj(ArcPoints, Point, ArcPoints)
endfor


return ()
gen_empty_obj(SinPoints)

get_contour_xld(ContCircle, Row, Col)


tuple_length(Row, Length)

angleTuple:=[]
for i := 1 to Length-1 by 1
    
    tuple_select(Row,i, y)
    tuple_select(Col, i,x)
    gen_cross_contour_xld(Point, y,x, 6+i*0.05, 0.785)  // 注意坐标顺序，先y后x
    
    angle_lx( y, x,row_center, col_center, Angle)
    angleTuple:=[angleTuple,Angle]
     concat_obj(SinPoints, Point, SinPoints)
endfor