排序——堆排序

原创于 2024-03-04 19:45:55 发布 · 1.1k 阅读

24 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #数据结构 #排序算法 #c语言

c语言知识点同时被 2 个专栏收录

38 篇文章

订阅专栏

数据结构代码与解释

17 篇文章

订阅专栏

本节继续复习排序算法。这次复习排序算法中的堆排序。堆排序属于选择排序。

什么是堆？

在复习堆排序之前，首先我们需要回顾一下什么是堆。

堆的本质其实是一个数组。它的物理结构本质上是一个数组。但是它的逻辑结构是一棵完全二叉树。我们在判断一个数组是否是一个堆的时候根据的就是它的逻辑结构。

那么怎么根据它的逻辑结构判断是否是一个堆。

首先堆的逻辑结构的二叉树的每一个孩子节点都大于它的每一个父亲，就是堆。这种堆叫做小堆。如果它的逻辑结构的每一个孩子节点都小于它的父亲节点。它同样是个堆，同时这种堆叫做大堆。

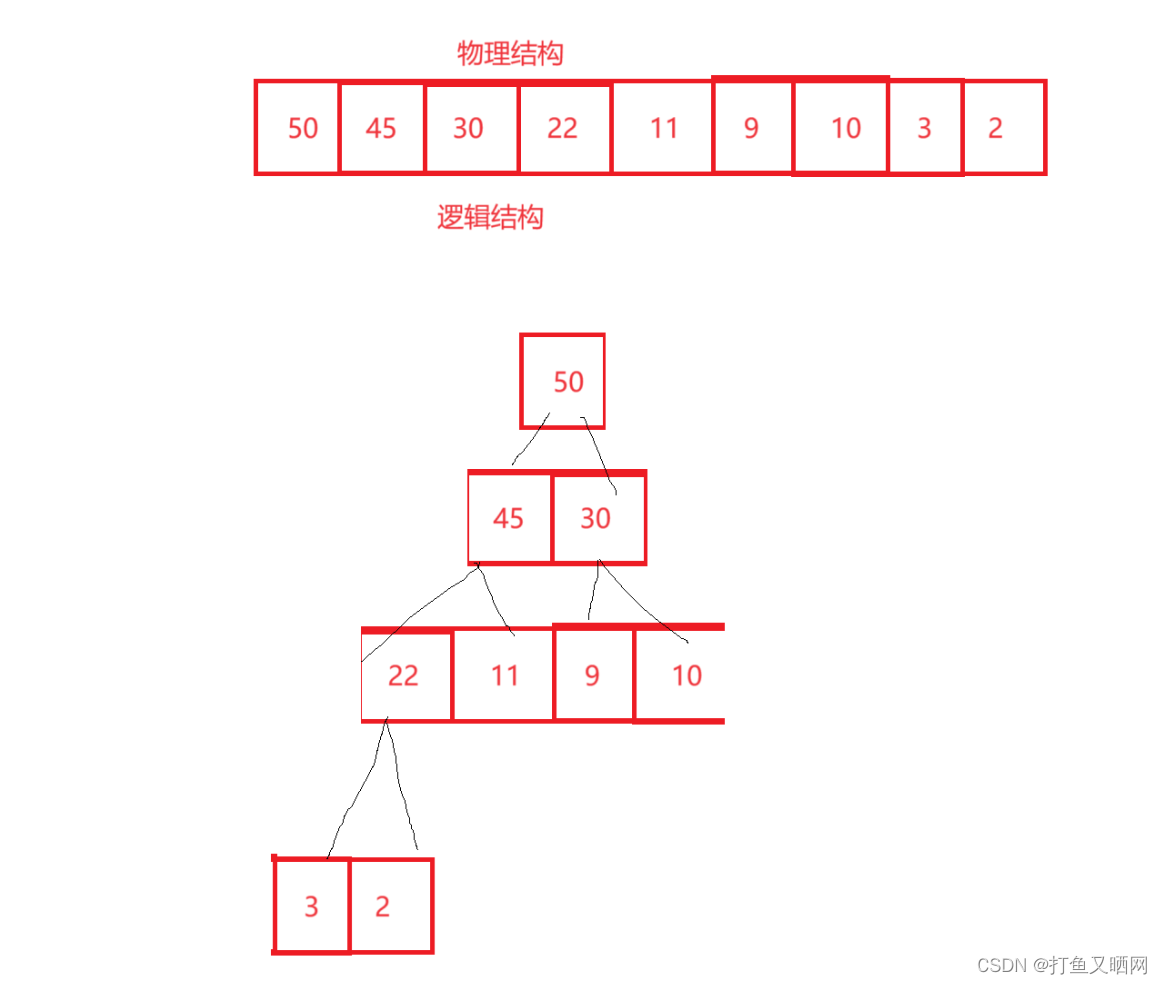
如图数组就是一个小堆

将该小堆的逻辑结构画出来就是这样的：

我们可以看到，在这棵二叉树之中的每一个父亲节点都小于它的孩子节点。那么他就是一个小堆。

大堆就是它的每个父亲节点都大于它的每个孩子节点

如图：

堆排序

堆排序的思想

堆排序的思想利用了大堆或小堆的结构。

我们从上面的解析可以发现。大堆中，第一个元素一定是整个数组中最大的那个元素；小堆中，第一个元素一定是数组中最小的那个元素。

堆排的核心就是每一趟都将堆的第一个元素和堆的最后一个元素交换位置。然后让这个堆的元素个数减一。同时通过向下调整算法重新建堆。循环往复。不断选出最大或者最小的那个数据放到堆的最后。

不知道向下调整算法可以去回顾本节：堆——c语言实现堆结构-优快云博客

现在我们来分析一下堆的排序过程。

我们使用小堆进行堆排：

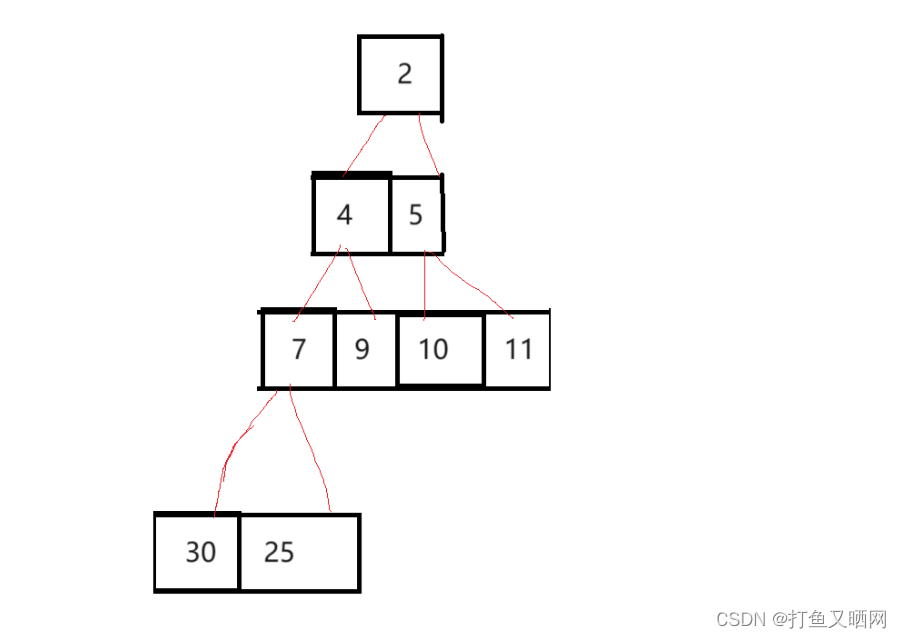
第一步，将第一个元素也就是堆顶的元素和最后一个元素交换：

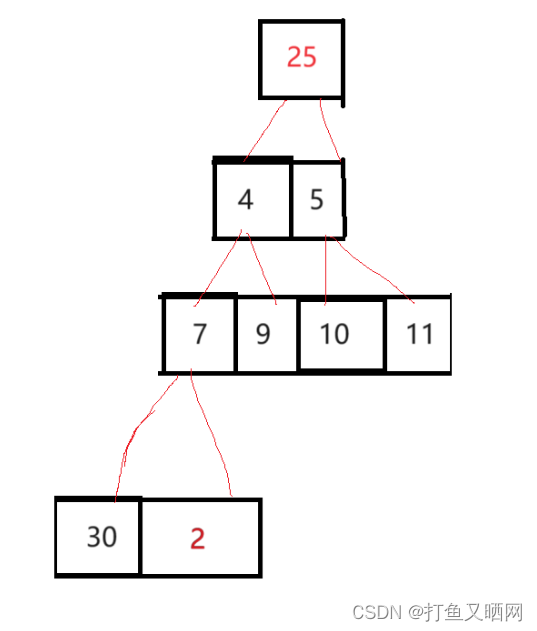
然后堆的大小减一：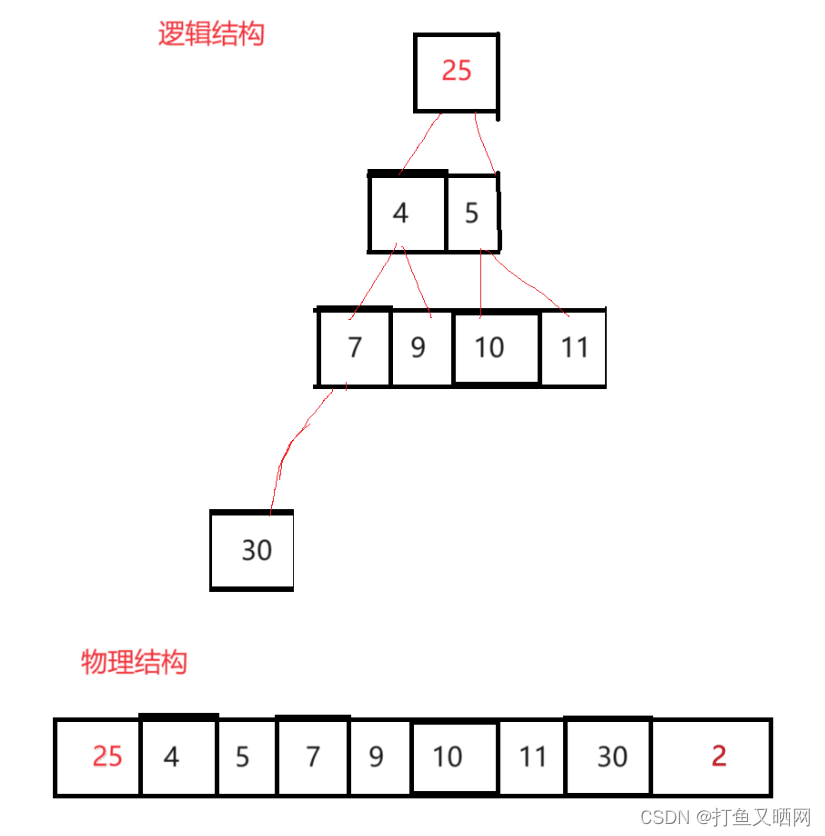

向下调整算法重新建堆：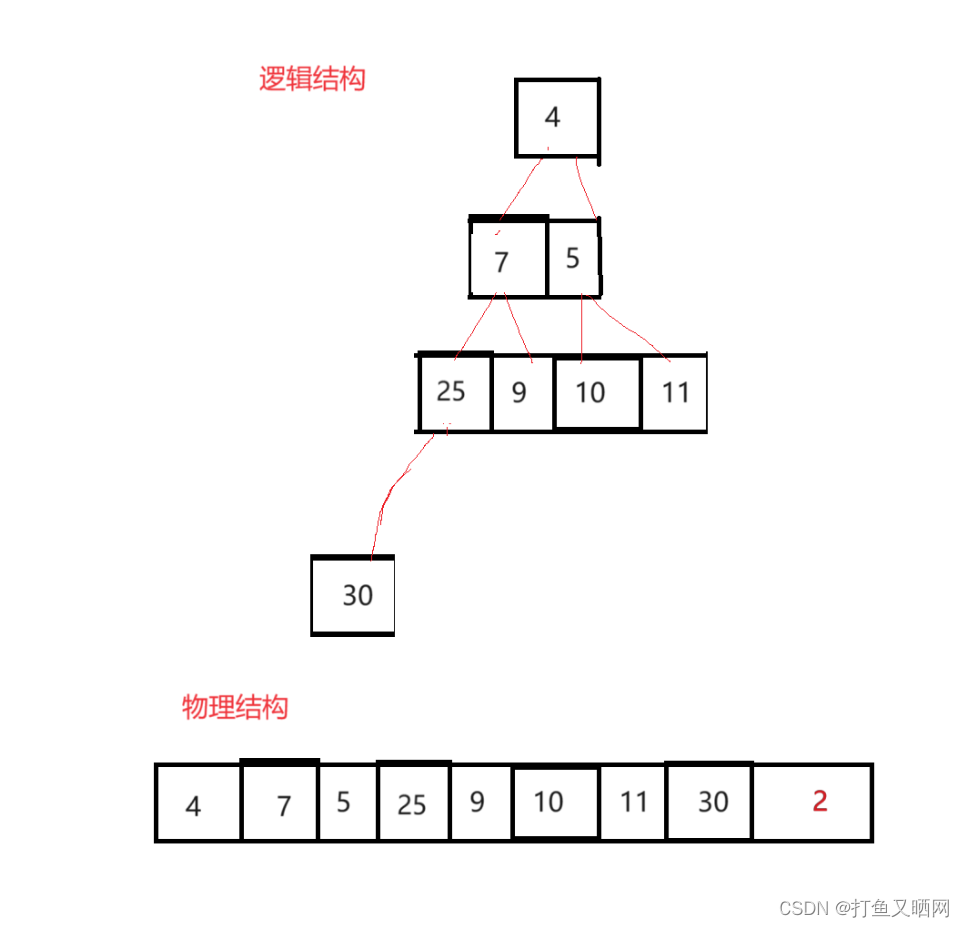

堆的第一个元素再次和堆最后一个元素交换位置：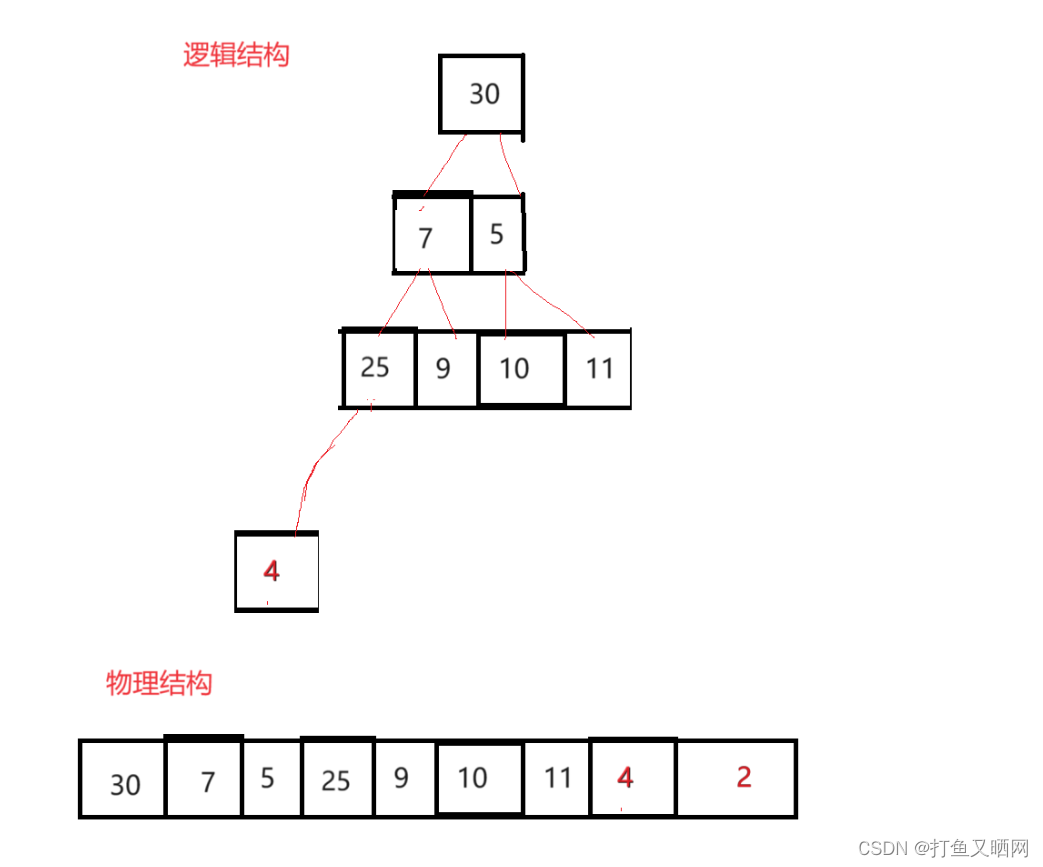

堆的大小减一：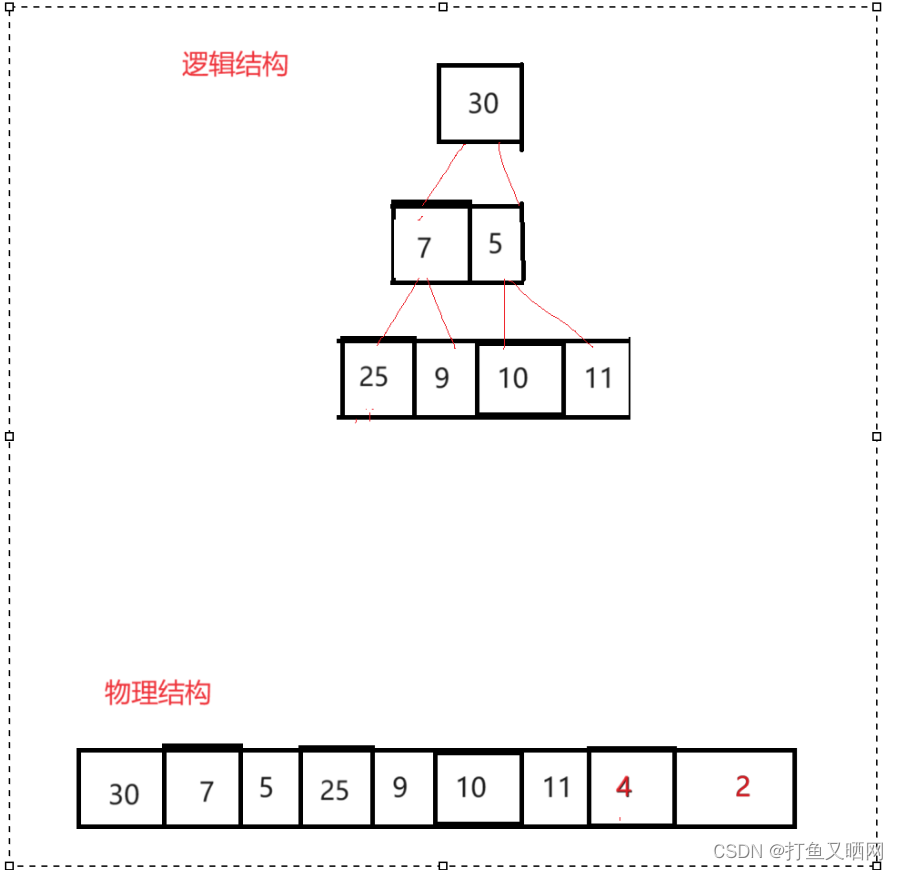

然后向下调整算法重新建堆：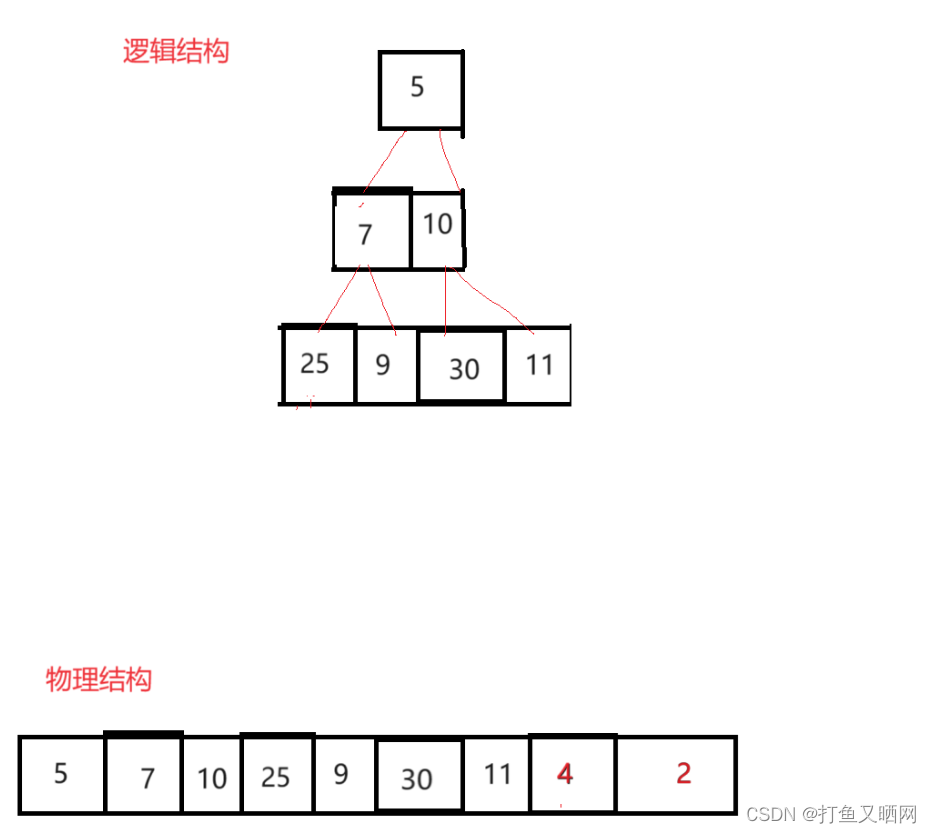

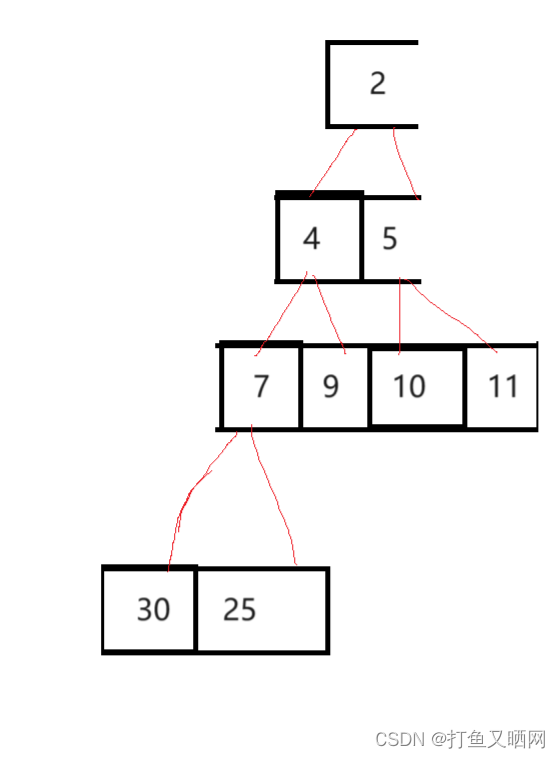
然后堆的第一个元素再和堆的最后一个元素交换位置，然后堆的大小减一，然后向下调整算法调堆。循环，一直到堆只剩下一个元素位置。排好后就是这样的：现在已经有序，同时是降序。这时我们使用的是小堆排的。其实这里就是用大小堆控制升序降序。小堆排的就是降序，大堆排的就是升序。

堆排代码

向下调整算法

我们先再来实现一次向下调整算法：

//向下调整建大堆。
void AdjustDownSort(int* a, int sz, int parent)
{

}
a是要建堆的数组， sz是数组的大小。 parent是建堆的堆顶节点

//向下调整建大堆。
void AdjustDownSort(int* a, int sz, int parent)
{
	int child = parent * 2 + 1;//先假设左孩子小。 

	
}
我们先假设左孩子比较大（注意，我这里要建的是大堆）。

//向下调整建大堆。
void AdjustDownSort(int* a, int sz, int parent)
{
	int child = parent * 2 + 1;//先假设左孩子小。 

	while (child < sz) //控制条件是孩子不能超出整个数据。 
	{
		
        child = 2 * parent + 1;
	}
}
然后使用child指针控制循环结束。当child指针超出整个数组的时候就不用再向下调整了。

//向下调整建大堆。
void AdjustDownSort(int* a, int sz, int parent)
{
	int child = parent * 2 + 1;//先假设左孩子小。 

	while (child < sz) //控制条件是孩子不能超出整个数据。 
	{
		if (child + 1 < sz && a[child] < a[child + 1])//让child指向大的那个孩子。说明建大堆， 排升序。 
		{
			child++;
		}
		
			child = 2 * parent + 1;

		

	}
}
因为我们是假设的左孩子比较大，所以进入循环之后我们要比较一下左右孩子。如果右孩子更大的话就假设错误， child指针需要加加。


//向下调整建大堆。
void AdjustDownSort(int* a, int sz, int parent)
{
	int child = parent * 2 + 1;//先假设左孩子小。 

	while (child < sz) //控制条件是孩子不能超出整个数据。 
	{
		if (child + 1 < sz && a[child] < a[child + 1])//让child指向大的那个孩子。说明建大堆， 排升序。 
		{
			child++;
		}
		//
		if (a[child] > a[parent]) 
		{
			Swap(&a[child], &a[parent]);
			parent = child;//继续向下调整。 父亲便孩子， 孩子变成孩子的孩子。
			child = 2 * parent + 1;

		}
		else 
		{
			break;//如果父亲比小的孩子还要大， 那么这个父亲就是一个堆。 就不需要再调整建堆了。
		}
		//

	}
}

然后在每次循环中都比较一下父亲节点和两个孩子中更小的节点。如果孩子比父亲还要大。就交换孩子节点和父亲节点。

如果孩子节点比父亲节点要小。那么就说明这个堆已经建好了。就跳出循环。

堆排整体

一、
//堆排序
void HeapSort(int* a, int sz) 
{
		
}
首先，堆排的函数名以及传参。除了快排传参基本都是传要排序的数组和数组的大小。

二、


//堆排序
void HeapSort(int* a, int sz) 
{
	int end = sz - 1;


	//先建堆， 向下调整建大堆
	for (int i = (end - 1) / 2; i >= 0; i--)//从最后一个节点的父亲开始向下调整。  一棵子树一棵子树的建成堆。最后整体成堆
	{
		AdjustDownSort(a, sz, i);//向下调整算法建大堆。
	}
	//

	while (end > 0) 
	{
		Swap(&a[0], &a[end]);//让第n个数据和堆顶最大的那个数据交换， 就能让第end个数据是最大的那个数据。 
		AdjustDownSort(a, end, 0);//第n个数据和堆顶数据交换后，前end - 1个数据只有堆顶不符合堆， 堆顶左右子树都是堆， 这时满足
		//向下调整算法。 然后向下调整。 
		end--;
	}
	
}