整数规划（一）

定义

部分或全部决策变量是整数的规划问题，称为整数规划。

如果模型是线性（一次，加减运算）的，则称为整数线性规划。

目标：

条件：

如果全部决策变量x取整数值，则称为全整数规划，反之，则称为混合整数规划。

如果决策变量只能取0 和1 ，则称为0-1规划。

整数线性规划的数学模型求解方法

整数规划对应的松弛问题就是决策变量从整数松弛到全部实数。

注意：整数规划的最优解不一定是再松弛问题的最优解的邻近整数解。

分支定界法

分支：从最优解的邻近整数分支开始进行分支。 用于缩小搜索范围

定界：更新目标函数的上界或下界。   用来剪支，提高搜索效率。

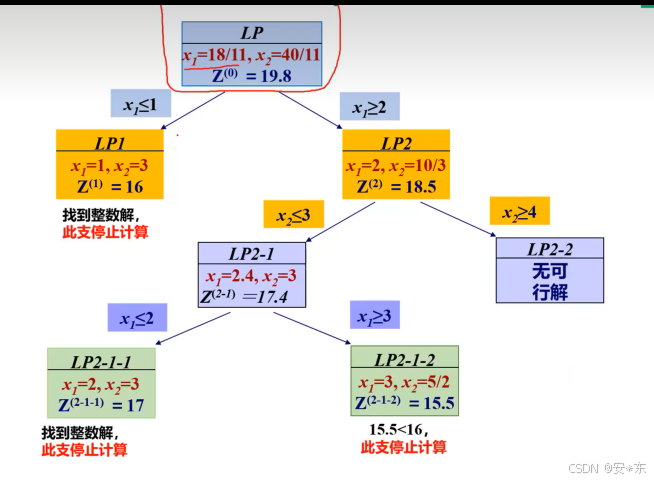
如图：

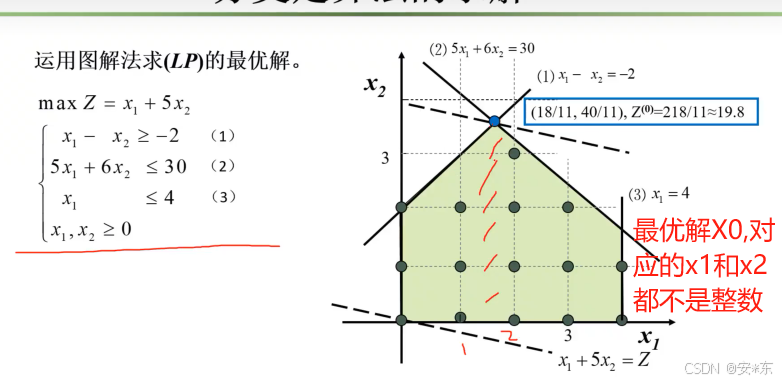
此时，最优解的初始上界为19.8。第一次分支，以x1为条件分为x1<=1和x1>=2。得到两个松弛子问题。

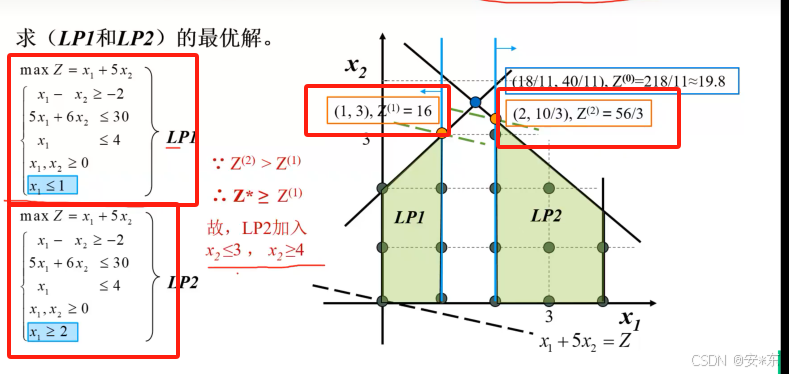
发现第一个子问题LP1的最优解为（1，3）目标值为16.此时16就作为目标值的一个下界，而LP2对应的最优解为（2，10/3）56/3 大于LP1.因此需要对LP2继续进行分支。以x2<=3,x2>=4作为分支条件，然后继续计算。

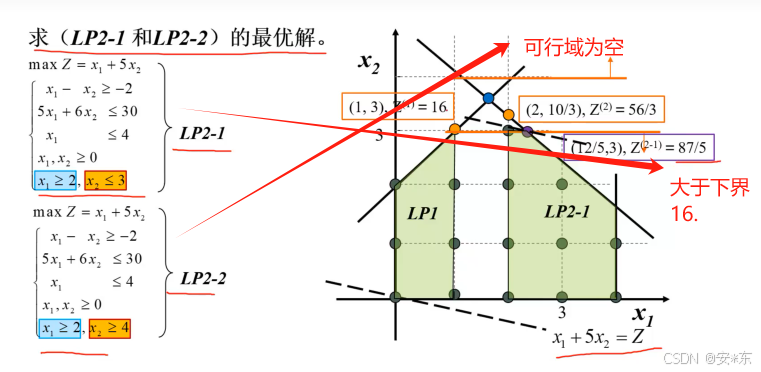
此时，我们发现，LP2-1的最优解大于下界 16.因此，需要继续分支。此时以x1<=2,x1>=3作为分支条件。

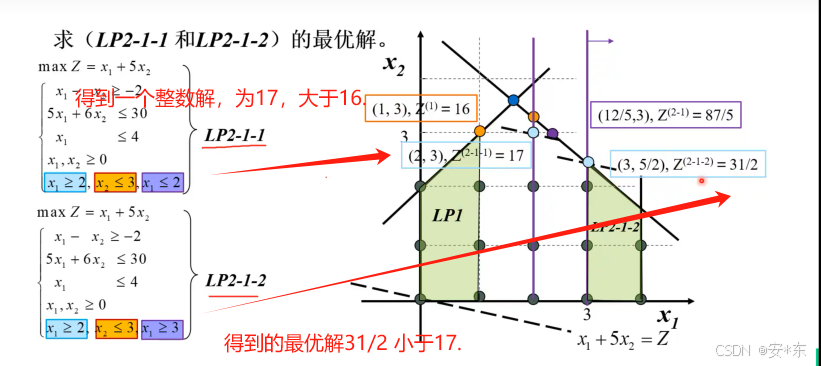
此时，由于LP2-1-2的最优解31/2 小于LP2-1-1的（整数）最优解17.因此没有必要再队LP2-1-2继续分支。（这就是定界提高搜索效率）

此时得到了目标函数的最优整数解（2，3） 17.