后缀自动机学习笔记

后缀自动机感觉比回文自动机和AC自动机难理解很多，我花了一个下午加一个晚上感觉还没有完全理解。
蒟蒻还是太菜了，但是我还是要写这篇博客，也希望能加深我的理解。

---

1.什么是后缀自动机

hihocoder的出题人很有良心，在一道题目里详解了什么是后缀自动机。想看的点这里。我也搬过来讲讲。

首先我们先把后缀自动机的图放出来，对于字符串S=”aabbabd”，它的后缀自动机是：（搬自hihocoder）

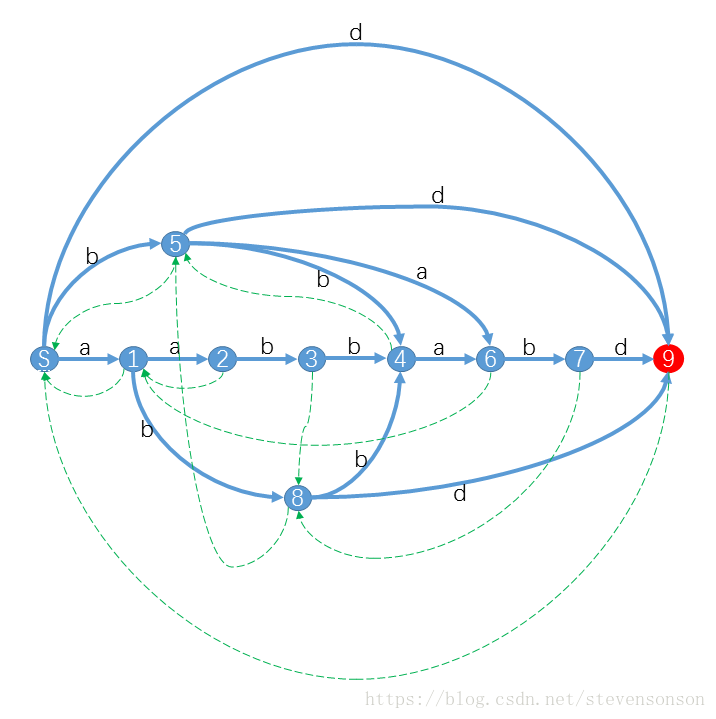
看起来十分的复杂，我们先不管绿线，只看蓝色的线，我们发现从S出发，沿着任意一条线走，一直走到T（图中的9），走出来的路径都是该字符串的后缀，不信可以试试看，举个例子：S5679对应的字符串是babd,就是aabbabd的后缀。
那么我们从S出发，沿着任意蓝线走，走到任意位置，走出的字符串都是该文本串的子串，比如S1846是abba，就是一个子串。
所以结合这张图，我们就能大概弄懂后缀自动机是个什么东西、它能干啥。

2.后缀自动机相关的一些东西

看上面的图，我们知道后缀自动机要构筑出所有的后缀，那么在构筑之前，我们要先看一些东西，以便后面理解。
首先一个概念是子串的位置结束集合。也就是一个子串，它在哪些位置结束过，比如对于aabbabd,那么子串ab的结束位置集合为{3,6}因为它在这样个位置都结束过，子串aabb的结束位置集合就只有{3}了。我们以endpos(s)表示s子串的结束位置集合。
我们把所有的子串的endpos都求出来，如果又两个子串的endpos相等，那么我们就把这两个子串的endpos归为一类。
那么接下去就有一个结论了，如果串s是串t的后缀，那么endpos(s) ⊇ endpos(t)，这个十分显然，因为只要t出现过的地方，s都出现过。而s出现过的地方，t并不一定出现过。并且还有一个结论，如果s不是t的后缀，那么 endpos(s) ∩ endpos(t) = ∅，这也非常显然。并且这两个命题的逆命题也一样成立。

那么我们就能发现一些性质了，endpos相同的子串集合一定是一些长度递减，并且长度短的为长度长的的后缀的一些子串。随便举个例子，就以endpos=6的集合为例，又哪些字符串呢？aabbab,abbab,bbab,bab。你看后面的串是前面的串的后缀，而且长度递减。
但是ab就不行了，因为ab在位置三出现过。所以我们发现对于每个endpos相同的集合，它里面的字符串的长度都是一段连续的数，对于endpos为i的集合，我们把子串长度最大的记为longest[i],最小的记为shortest[i],那么shortest[i]肯定等于某个longest[j]+1,比如我们前面endpos为6的集合的shortest就是endpos为{3，6}的集合的longest加一。

如果shortest[i]=longest[j]+1，那么我们就记fa[i]=j,那大家可以发现，我们上图中绿色的连线其实就是fa这个数组的连线，而图中每个点代表的endpos集合就是从S走到这个点的字符串的endpos。

如果我们遮掉蓝色的边不看，只看绿色的边，我们会发现其实这是个树形结构，对于这棵树，我们称之为parent树，这棵树在构建后缀自动机的时候又很大的用处。

3.后缀自动机的构建

下面最重要的部分后缀自动机的构建要来了。对于构建，我们要分三种情况：

1°

假设我们要加入的字符为c，它是第p个点。而在之前加入的字符中没有出现过c，那么怎么办呢，我们先找到上一个出现的字符，然后一直往回跳它们的fa,知道跳到S点，然后把这些点的c儿子都赋值为p，最后fa[p]=1即可。

    while(f&&!son[f][c]) son[f][c]=p,f=fa[f];
    if(!f){fa[p]=1;return;} //为什么fa[p]等于1？因为在以p结尾的endpos中，p是最短的，shortest为1，
    //而1（也就是空节点）的longest为0，所以fa[p]=1

这种情况还是比较简单的。
而如果出现过c字符，那么我们的f会在某一个地方停下来。

2°

这种情况也比较特殊，就是前面加入的字符串的所有字符都为c，比如之前的字符串为aaa,现在又加入字符a。
那么这个时候会出现什么情况呢？设x为son[f][c]，那么$longest(f)+1=shortest(x)=longest(x)$，因为只有从s到我们要加入字符的地方所有的字符都一样时，整个自动机才会只有一条路径。（比如如果串是aaa,那么自动机就是一条aaa的链。但如果串是aab，那么串除了是aab的链以外，还会有一条从S连到b的路径，那么这时候上式就不成立了）
那么这个时候直接让fa[p]=x即可。

    int x=son[f][c]；
    if(len[x]==len[f]+1){
        fa[p]=x;return;
    }

3°

那么剩下的情况，也就是$longest(f)+1=shortest(x)=longest(x)$不成立时的情况就是第三种情况了。
那么这时的操作比较复杂：

把x节点复制一遍给y，所有前面连续的一段本应该连向x的都连向y（也就是说在A前面可能还有连向x的边），所有从x连出去的边都连向y，把x和p的parent父亲连向y，把y的len设置为len[f]+1。

这么说可能大家有点懵逼，所以结合代码和举例子，可以再理解一下：

    int y=++node,x=son[f][c];
    fa[y]=fa[x];fa[x]=fa[p]=y;len[y]=len[f]+1;
    memcpy(son[y],son[x],sizeof(son[y]));
    while(f&&son[f][c]==x) son[f][c]=y,f=fa[f];

我们以aaabb为例：
首先添加a，属于情况1，直接连即可。后面两次添加a，都属于情况2，比较简单。然后第一次添加b，又是情况1。然后当我们添加第二个b时，这个b的父亲是第一个b。那么我们就按照上述方法进行复制和置换。那么S相连的b就成了复制的b，但第三个a相连的b依旧是第一个b。而第一个b的父亲变成了复制的b。然后它们(第一个b和我们复制的b)的儿子是第二个b，而第二个b的父亲是第一个b。

大家发现这样改动的根本意义是改变了第一个b的父亲。因为在加入一个字符后，第一个b的endpos集合会变，所以需要一个新的点来帮助维护正确的parent树。

讨论完这三种情况后，我们构建就完成了。

---

模板

洛谷的板子题

代码如下：

#include<bits/stdc++.h>
#define MAXN 2000005
#define ll long long
using namespace std;
int read(){
    char c;int x;while(c=getchar(),c<'0'||c>'9');x=c-'0';
    while(c=getchar(),c>='0'&&c<='9') x=x*10+c-'0';return x;
}
string s;
int lst=1,node=1,son[MAXN][26],fa[MAXN],len[MAXN],siz[MAXN],A[MAXN],t[MAXN];
ll ans;
void SAM(int c){
    int f=lst,p=++node;lst=p;
    len[p]=len[f]+1;siz[p]=1;
    while(f&&!son[f][c]) son[f][c]=p,f=fa[f];
    if(!f){fa[p]=1;return;}  //situation 1
    int x=son[f][c],y=++node;
    if(len[x]==len[f]+1){  //situation 2
        fa[p]=x;node--;return;
    }
    fa[y]=fa[x];fa[x]=fa[p]=y;len[y]=len[f]+1;  //situation 3
    memcpy(son[y],son[x],sizeof(son[y]));
    while(f&&son[f][c]==x) son[f][c]=y,f=fa[f];
}
int main()
{
    cin>>s;
    for(int i=0;i<s.size();i++) SAM(s[i]-'a');
    for(int i=1;i<=node;i++) t[len[i]]++;
    for(int i=1;i<=node;i++) t[i]+=t[i-1];
    for(int i=1;i<=node;i++) A[t[len[i]]--]=i;
    for(int i=node;i;i--){  //由于题目要求，将所有的len进行基数排序，然后从parent树上从后到前（类似于dfs）的思想统计答案
        int now=A[i];siz[fa[now]]+=siz[now];
        if(siz[now]>1) ans=max(ans,1ll*siz[now]*len[now]);
    }
    printf("%lld\n",ans);
    return 0;
}