探索和推导OpenGL中GLFrustum()投影矩阵的时候想到的一个“结论”,虽然不是很复杂,但是推导起来用到了代数射影几何、线性代数里的一些基础知识,用Geogebra生成动态图演示一下。
其实是一系列问题:
- 平面上存在唯一的线性映射MMM,把矩形ABCDABCDABCD映射为顶点坐标如图、边长为2的小正方形A′B′C′D′A'B'C'D'A′B′C′D′;
- 设置矩形ABCDABCDABCD的四个顶点坐标,使得 l≤−1,b≤−1l\le-1,b\le-1l≤−1,b≤−1, r≥1,t≥1r\ge 1, t\ge 1r≥1,t≥1。 求证线性映射MMM有唯一的不动点在小正方形A′B′C′D′A'B'C'D'A′B′C′D′之内;或者,求小正方形A′B′C′D′A'B'C'D'A′B′C′D′之内的线性映射MMM的不动点坐标。
这个问题有一定计算量;我给出的解答,基于代数射影几何、线性代数、矩阵的特征向量和特征值等。
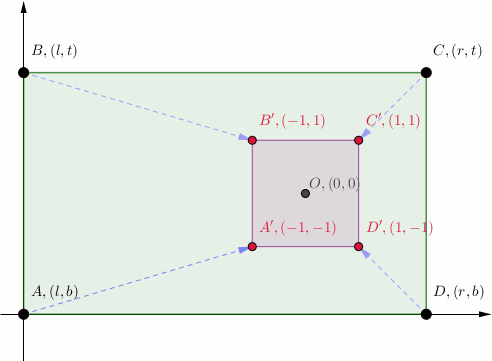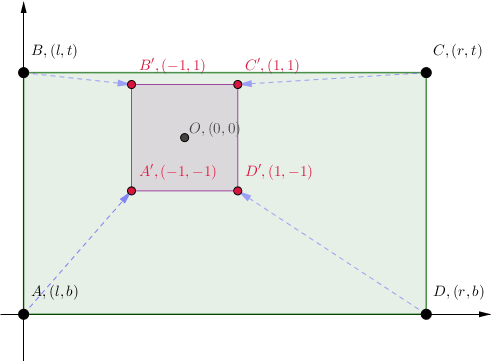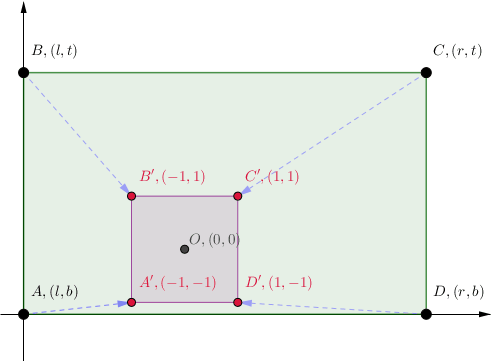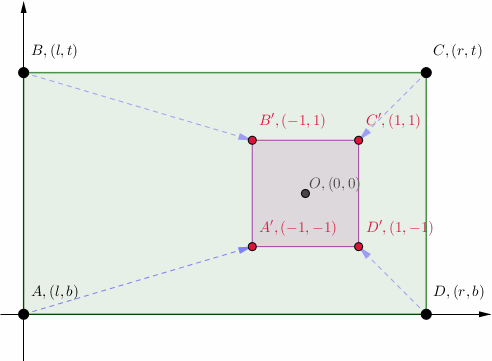








 探讨OpenGL中GLFrustum()投影矩阵的推导,涉及代数射影几何与线性代数原理。解析平面上唯一线性映射,将矩形映射为特定小正方形,并寻找其在小正方形内的唯一不动点。
探讨OpenGL中GLFrustum()投影矩阵的推导,涉及代数射影几何与线性代数原理。解析平面上唯一线性映射,将矩形映射为特定小正方形,并寻找其在小正方形内的唯一不动点。
















 337
337

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








