机器学习：支持向量机（下）

非线性支持向量机

模型

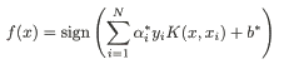
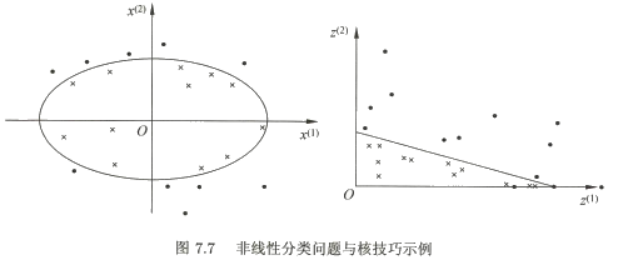
非线性问题往往不好求解，所以希望能用解线性分类问题的方法解决这个问题。所采取的方法是进行一个非线性变换，将非线性问题变换为线性问题，通过解变换后的线性问题的方法求解原来的非线性问题。对图7.7所示的例子，通过变换，将左图中椭圆变换成右图中的直线，将非线性分类问题变换为线性分类问题。 

 

 核技巧其实就是做一种非线性变换，把原来的输入数据转换成新数据。新得到的特征集合被称为特征空间。

 在线性支持向量机中的模型定义为

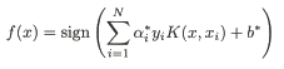
我们注意到在线性支持向量机的对偶问题中，无论是目标函数还是决策函数（分离超 平面）都只涉及输入实例与实例之间的内积。在对偶问题的目标函数（7.37）中的内积xi·xj可以用核函数K(xi，xj)＝Ø(xi)·Ø(xj)来代替。此时对偶问题的目标函数成为  

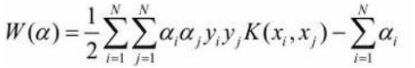
同样，分类决策函数中的内积也可以用核函数代替，而分类决策函数式成为  

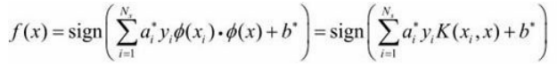
这等价于经过映射函数Ø将原来的输入空间变换到一个新的特征空间，将输入空间中的内积xi·xj变换为特征空间中的内积Ø(xi)·Ø(xj)，在新的特征空间里从训练样本中学习线性支持向量机。当映射函数是非线性函数时，学习到的含有核函数的支持向量机是非线性分类模型。

也就是说，在核函数K(x,z)给定的条件下，可以利用解线性分类问题的方法求解非线性分类问题的支持向量机。学习是隐式地在特征空间进行的，不需要显式地定义映射函数。这样的技巧称为核技巧，它是巧妙地利用线性分类学习方法与核函数解决非线性问题的技术。在实际应用中，往往依赖领域知识直接选择核函数，核函数选择的有效性需要通过实验验证。

其实就是把线性支持向量机模型中的x·xi的内积用和的内积来替代，这样就把原输入数据进行了非线性变化。

 

 

 

 求解第一步的时候，这类问题通常的解法是用 序列极小优化（Sequential Minimal Optimization，SMO）算法。SMO算法把优化问题分解成一系列 最小化子问题，可以通过解析方法解决。