数据结构个人笔记整理1：线性结构（个人复习学习使用，如有错误欢迎指正感谢）C语言版本

一、线性表

定义：线性表（ linear list）是n个具有相同特性的数据元素的有限序列。线性表是⼀种在实际中⼴泛使⽤的数据结构，常⻅的线性表：顺序表、链表、栈、队列、字符串...
线性表在逻辑上是线性结构，也就说是连续的⼀条直线。但是在物理结构上并不⼀定是连续的，线性
表在物理上存储时，通常以数组和链式结构的形式存储。

本质：

数据按顺序排列，有明确的前后关系，每个元素只有唯一的前驱和后继（除了第一个和最后一个）

1.1顺序表

•实现方式

用连续内存存储，支持快速随机访问，访问时间O(1)

插入和删除时，后续元素需整体移动，时间复杂度O（n）

动态扩容通常采用倍增策略，避免频繁扩容带来的性能损耗

动态顺序表的实现：

//定义动态顺序表的结构
typedef int SLDataType;
typedef struct SeqList
{
	SLDataType* arr;
	int size;      //有效数据个数
	int capacity;  //空间容量
}SL;

✿：

typedef int SLDataType的作用：

定义一个新的类型别名SLDataType，实际上是int类型，这样做是为了方便以后修改存储的数据类型（只需改这一处）

典型操作

头文件

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>

//定义动态顺序表的结构
typedef int SLDataType;
typedef struct SeqList
{
	SLDataType* arr;
	int size;      //有效数据个数
	int capacity;  //空间容量
}SL;

//typedef struct SeqList SL;

/*
SL* ps 的含义
SL* 是指针类型，表示指向 SL 结构体的指针。
ps 是参数名*/

void SLPrint(SL* ps);
//初始化
void SLInit(SL* ps);
//销毁
void SLDestroy(SL* ps);

//尾插
void SLPushBack(SL* ps, SLDataType x);
//头插
void SLPushFront(SL* ps, SLDataType x);
//尾删
void SLPopBack(SL* ps);
//头删
void SLPopFront(SL* ps);

//指定位置之前插⼊数据
void SLInsert(SL* ps, int pos, SLDataType x);
// 删除POS位置的数据
void SLErase(SL* ps, int pos);
//查找
int SLFind(SL* ps, SLDataType x);

初始化和销毁

//初始化
void SLInit(SL* ps)
{
	ps->arr = NULL;
	ps->size = ps->capacity = 0;
}


// 销毁（释放内存）

void SLDestroy(SL* ps)
{
	assert(ps);
	if (ps->arr)// 检查数组是否已分配内存
		free(ps->arr);// 释放动态分配的内存
	ps->arr = NULL;
	ps->size = ps->capacity = 0;
}

动态扩容

一个“自我升级”的容器，在装满时会自动“变大”，就像行李箱拉链外扩一样，保证你插入元素时永远有空间

// 动态扩容
void SLCheckCapacity(SL* ps)
{
	if (ps->size == ps->capacity)// 判断是否要扩容
	{

        //计算新的容量，倍增
		int newCapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
		

		//realloc第二个参数，单位是字节
		SLDataType* tmp = (SLDataType*)realloc(ps->arr, newCapacity * sizeof(SLDataType));

		// 错误处理：内存分配失败的情况
        if (tmp == NULL)
		{
			perror("realloc fail!");
			exit(1);
		}

        // 更新数组指针和容量信息
		ps->arr = tmp;
		ps->capacity = newCapacity;
	}
}

知识点复习：

-> 操作符：用于通过指针访问结构体成员

比如：ps->arr

这里ps->arr 表示访问 ps 所指向的结构体中的 arr 成员

查找

int SLFind(SL* ps, SLDataType x)
{
	for (int i = 0; i < ps->size; i++)
	{
		if (ps->arr[i] == x)
		{
			//找到了
			return i;
		}
	}
	//未找到
	return -1;
}

头部插入/删除

时间复杂度：O(n)  每次插入/删除都需移动所有元素。

//头插
void SLPushFront(SL* ps, SLDataType x)
{
	
	assert(ps != NULL);
	//判断空间是否足够
	SLCheckCapacity(ps);
	//将顺序表中所有数据向后挪动一位
	for (int i = ps->size; i > 0; i--)
	{
		ps->arr[i] = ps->arr[i - 1];
	}
	ps->arr[0] = x;
	++ps->size;
}


//头删
void SLPopFront(SL* ps)
{
	assert(ps && ps->size);// 确保指针有效且表非空
	for (int i = 0; i < ps->size-1; i++)
	{
		ps->arr[i] = ps->arr[i + 1];
	}
	--ps->size;
}

尾部插入/删除

//尾插
void SLPushBack(SL* ps, SLDataType x)
{
	//判断空间是否足够
	if (ps->size == ps->capacity)
	{
		int newCapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
		//增容
		//realloc第二个参数，单位是字节
		SLDataType* tmp = (SLDataType*)realloc(ps->arr, newCapacity*sizeof(SLDataType));
		if (tmp == NULL)
		{
			perror("realloc fail!");
			exit(1);
		}
		ps->arr = tmp;
		ps->capacity = newCapacity;
	}
	//空间足够的情况下
	ps->arr[ps->size++] = x;
}

//销毁链表
void SListDestroy(SLTNode** pphead)
{
	SLTNode* pcur = *pphead;
	while (pcur)
	{
		SLTNode* next = pcur->next;
		free(pcur);
		pcur = next;
	}
	*pphead = NULL;
}

典型应用：

顺序表适合元素个数变化不大、访问频繁的场景

1.频繁访问元素的场景，比如数组查表：

•学生成绩列表、商品编号数组等

•支持随机访问：O（1）时间访问第i个元素

2.存储静态数据集合：

•数据元素个数已知，变化不大。比如阅读销售额统计度

•插入/删除操作少，读操作多。

3.需要支持二分查找的情况：

•顺序表天然支持通过下标快速定位，可用于排序后查找。

二、链表（Linked  List）

2.1概念和本质

•链表是链表是⼀种物理存储结构上⾮连续、⾮顺序的存储结构，通过指针链接的数据结构，每个节点包含和指向下一节点的指针。

•不同于顺序表，链表在内存中不连续存储，可以高效插入和删除。

 当然，链表中的“节点”是最核心的基本单位，这里要着重提一下。

节点（Node）

在链表中，节点是链表的基本组成单位，每个节点都包含两部分：

1.数据域（data）：用于存放具体的数据内容。

2.指针域（next/prev）:用于指向下一个或上一个节点的地址，实现节点之间的连接。

2.2分类

•单链表（Singly Linked List）

•双向链表(Doubly Linked List)

•循环链表（Circular Linked List）

链表的实现

1.单链表：

//定义链表的结构---结点的结构
typedef int SLTDataType;
typedef struct SListNode {
	SLTDataType data;//存储的数据
	struct SListNode* next; //指向下一个结点
}SLTNode;

//typedef struct SListNode SLTNode;

2.双向链表

//双向链表的结构
typedef int LTDataType;
typedef struct ListNode {
	LTDataType data;
	struct ListNode* next;
	struct ListNode* prev;
}LTNode;

循环链表因其与普通链表结构差异不大，仅在尾指针指向头节点以实现循环，因此在此笔记中不做详细展开，实际使用时可在单/双链表基础上灵活改造

典型操作

一、单链表：

不带头单向不循环链表

头文件：

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>

//定义链表的结构---结点的结构
typedef int SLTDataType;
typedef struct SListNode {
	SLTDataType data;//存储的数据
	struct SListNode* next; //指向下一个结点
}SLTNode;

//typedef struct SListNode SLTNode;

//链表的打印
void SLTPrint(SLTNode* phead);

//尾插
void SLTPushBack(SLTNode** pphead, SLTDataType x);
//头插
void SLTPushFront(SLTNode** pphead, SLTDataType x);
//尾删
void SLTPopBack(SLTNode** pphead);
//头删
void SLTPopFront(SLTNode** pphead);
//查找
SLTNode* SLTFind(SLTNode* phead, SLTDataType x);

//在指定位置之前插⼊数据
void SLTInsert(SLTNode** pphead, SLTNode* pos, SLTDataType x);
//在指定位置之后插⼊数据
void SLTInsertAfter(SLTNode* pos, SLTDataType x);

//删除pos结点
void SLTErase(SLTNode** pphead, SLTNode* pos);
//删除pos之后的结点
void SLTEraseAfter(SLTNode* pos);

//销毁链表
void SListDestroy(SLTNode** pphead);

链表节点创建

动态创建一个新的链表节点，初始化其数据域并将指针域置为 NULL，最后返回指向该节点的指针。

SLTNode* SLTbuyNode(SLTDataType x)
{
	//根据x创建节点
	SLTNode* newnode = (SLTNode*)malloc(sizeof(SLTNode));//动态分配内存创建新节点
	//检查是否创建成功
    if (newnode == NULL)
	{
		perror("malloc fail!");
		exit(1);
	}
    //初始化节点数据
	newnode->data = x;
	newnode->next = NULL;

    //返回新节点指针
	return newnode;
}

链表的打印

//链表的打印
void SLTPrint(SLTNode* phead)
{
	SLTNode* pcur = phead;//一开始将指针置为空
	while (pcur)
	{
		printf("%d -> ", pcur->data);
		pcur = pcur->next;//移动指针到下一节点
	}
	printf("NULL\n");
}

尾插&尾删

// 尾插：在链表尾部插入新节点
void SLTPushBack(SLTNode** pphead, SLTDataType x)
{
    // 断言检查：确保头指针地址有效（防止传入NULL）
    assert(pphead);
    
    // 创建新节点（调用之前实现的节点创建函数）
    SLTNode* newnode = SLTbuyNode(x);
    
    // 情况1：链表为空
    if (*pphead == NULL)
    {
        // 直接将新节点作为头节点（需通过二级指针修改头指针）
        *pphead = newnode;
    }
    else {
        // 情况2：链表不为空，需要找到尾节点
        
        // 遍历指针，初始指向头节点
        SLTNode* ptail = *pphead;
        
        // 循环找到尾节点（next为NULL的节点）
        while (ptail->next)
        {
            ptail = ptail->next;
        }
        
        // 将尾节点的next指向新节点，完成插入
        ptail->next = newnode;
    }
}

// 尾删：删除链表的尾节点
void SLTPopBack(SLTNode** pphead)
{
    // 断言检查：确保头指针地址有效且链表不为空
    assert(pphead && *pphead);
    
    // 情况1：链表只有一个节点
    if ((*pphead)->next == NULL)
    {
        // 释放该节点内存，并将头指针置为NULL
        free(*pphead);
        *pphead = NULL;
    }
    else {
        // 情况2：链表有多个节点，需要找到尾节点及其前驱
        
        // prev记录尾节点的前一个节点（初始为NULL）
        SLTNode* prev = NULL;
        
        // ptail遍历指针，初始指向头节点
        SLTNode* ptail = *pphead;
        
        // 循环找到尾节点和其前驱
        // 退出时，ptail指向尾节点，prev指向其前驱
        while (ptail->next)
        {
            prev = ptail;
            ptail = ptail->next;
        }
        
        // 将前驱节点的next置为NULL，断开与尾节点的连接
        prev->next = NULL;
        
        // 释放尾节点内存，并置为NULL防止野指针
        free(ptail);
        ptail = NULL;
    }
}

头插&头删

// 头插：在链表头部插入新节点
void SLTPushFront(SLTNode** pphead, SLTDataType x)
{
    // 断言检查：确保头指针地址有效（防止传入NULL）
    assert(pphead);
    
    // 创建新节点（数据为x，next初始化为NULL）
    SLTNode* newnode = SLTbuyNode(x);
    
    // 步骤1：新节点的next指向原头节点
    newnode->next = *pphead;
    
    // 步骤2：更新头指针，使其指向新节点
    *pphead = newnode;
}
// 头删：删除链表的头节点
void SLTPopFront(SLTNode** pphead)
{
    // 断言检查：确保头指针地址有效且链表不为空
    assert(pphead && *pphead);
    
    // 保存原头节点的下一个节点
    SLTNode* next = (*pphead)->next;
    
    // 释放原头节点的内存
    free(*pphead);
    
    // 更新头指针，指向原头节点的下一个节点
    *pphead = next;
}

头尾增删时间复杂度

操作	时间复杂度	原因
头插法	O(1)	直接修改头指针，无需遍历
头删法	O(1)	直接修改头指针，无需遍历
尾插法	O(n)	需要遍历到尾节点
尾删法	O(n)	需要遍历到尾节点的前驱节点

这里涉及一个链表的重要考点：指针操作顺序，尤其是在头插法和头删法中，指针修改顺序直接影响正确性

1. 头插法的指针顺序

void SLTPushFront(SLTNode** pphead, SLTDataType x)
{
    SLTNode* newnode = SLTbuyNode(x);
    newnode->next = *pphead;  // 步骤1
    *pphead = newnode;        // 步骤2
}

正确顺序：

1.新节点的next指向原头节点

2.更新头节点指向新节点

错误顺序（先更新头指针）

后果：头指针->next被覆盖成了新的节点，原来的Node1入口就彻底丢失了，先让新节点的next指向原头节点使得原头节点得以保存。

2. 头删法的指针顺序

void SLTPopFront(SLTNode** pphead)
{
    SLTNode* next = (*pphead)->next;  // 步骤1
    free(*pphead);                    // 步骤2
    *pphead = next;                   // 步骤3
}

正确顺序：

1.保存原头节点的下一个节点

2.释放原头节点内存

3.更新头指针指向下一个节点

错误顺序（先释放内存）：

后果：释放内存后再访问原头节点的next，引发野指针错误。

3. 核心原理

• 头插法：必须先连接新节点与原链表，再更新头指针，避免丢失原链表。
• 头删法：必须先保存后继节点，再释放当前节点，避免无法访问后继节点

 在指定位置前/后插入元素

//在指定位置之前插⼊数据
void SLTInsert(SLTNode** pphead, SLTNode* pos, SLTDataType x)
{
	assert(pphead && pos);
	//当pos指向第一个结点，是头插
	if (pos == *pphead)
	{
		SLTPushFront(pphead, x);
	}
     // 验证是否找到pos
    assert(pos);

	else {
		SLTNode* newnode = SLTbuyNode(x);// 创建新节点并赋值
		//找pos的前一个结点
		SLTNode* prev = *pphead;
		while (prev->next != pos)//只要当前节点的下一个节点不是目标位置 pos，就继续遍历
		{
			prev = prev->next;//每次循环将 prev 移动到下一个节

		}
		
       // 执行插入操作：prev -> newnode -> pos
		prev->next = newnode;
		newnode->next = pos;
	}
}


//在指定位置之后插⼊数据
void SLTInsertAfter(SLTNode* pos, SLTDataType x)
{
    //验证是否找到pos
	assert(pos);
    //创建新节点并初始化数据
	SLTNode* newnode = SLTbuyNode(x);

	// 1. 让新节点指向pos的下一个节点

	newnode->next = pos->next;
   // 2. 让pos指向新节点
	pos->next = newnode;
}

删除pos节点&pos之后的节点

//删除pos结点
void SLTErase(SLTNode** pphead, SLTNode* pos)
{
	assert(pphead && pos);
	//pos就是头结点，调用头删函数
	if (pos == *pphead)
	{
		SLTPopFront(pphead);
	}

	else {
        // 查找pos的前一个节点
		SLTNode* prev = *pphead;
		while (prev->next != pos)
		{
			prev = prev->next;
		}
		// 调整指针：跳过pos节点，将前一个节点直接连接到pos的下一个节点
        // prev -> pos -> pos->next 变为 prev -> pos->next
		prev->next = pos->next;
		free(pos);
		pos = NULL;
	}
}
//删除pos之后的结点
void SLTEraseAfter(SLTNode* pos)
{
	assert(pos && pos->next);
     // 标记待删除的节点：pos的下一个节点
	//pos del del->next
	SLTNode* del = pos->next;

   //1：将pos的next指针跳过del节点，直接指向del的下一个节点
	pos->next = del->next;
  //2：释放待删除节点的内存，防止内存泄漏
	free(del);
	del = NULL;
}

销毁链表

void SListDestroy(SLTNode** pphead)
{
	SLTNode* pcur = *pphead;
	while (pcur)
	{   // 1. 保存当前节点的下一个节点指针，防止释放当前节点后无法访问后续节点
		SLTNode* next = pcur->next;
        // 2. 释放当前节点的内存
		free(pcur);
        // 3. 移动到下一个节点继续处理
		pcur = next;
	}
	*pphead = NULL;
}

单链表的典型应用

单链表适合插入和删除操作频繁，尤其是中间位置的场景

1.实现栈或队列

•函数调用栈、任务队列等（尾插/头删效率高）

2.插入/删除频繁的动态集合：

3.不需要随机访问的场景

•按顺序处理数据流或日志链表，逐个节点遍历处理

4.大数据量或内存碎片多时

双向链表

带头双向循环链表

头文件

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

//双向链表的结构
typedef int LTDataType;
typedef struct ListNode {
	LTDataType data;
	struct ListNode* next;//指向下一个节点
	struct ListNode* prev;//指向前一个节点
}LTNode;


void LTPrint(LTNode* phead);
//双向链表的初始化
//void LTInit(LTNode** pphead);

LTNode* LTInit();
//传二级：违背了接口一致性
//void LTDesTroy(LTNode** pphead);
//传一级：调用完成之后将实参手动置为NULL（推荐）
void LTDesTroy(LTNode* phead);

//头结点要发生改变，传二级
// 头结点不发生改变，传一级
//尾插
void LTPushBack(LTNode* phead, LTDataType x);
//头插
void LTPushFront(LTNode* phead, LTDataType x);

bool LTEmpty(LTNode* phead);
//尾删
void LTPopBack(LTNode* phead);
//头删
void LTPopFront(LTNode* phead);

LTNode* LTFind(LTNode* phead, LTDataType x);
//在pos位置之后插⼊数据
void LTInsert(LTNode* pos, LTDataType x);
//课下练习——在指定位置之前插入数据

//删除pos位置的结点
void LTErase(LTNode* pos);

为何情况不同要用不同级指针传头节点呢？

•当操作会改变头指针本身（如初始化、头插、头删等），需要传递头指针的地址（二级指针）

•当操作不改变头指针本身（如遍历、查找、销毁等），传递头指针的值（一级指针）即可

补充复习：一级指针&二级指针

一、一级指针（普通指针）

1. 定义与本质

• 一级指针是指向普通变量的指针，存储的是变量的内存地址。

• 例如：int* p = &a; 表示 p 指向 int 类型变量 a 的地址。

2. 典型用法

• 访问和修改目标变量的值：通过 *p 解引用操作。

• 动态内存分配：如 malloc() 返回的是一级指针。

• 函数参数传递（值传递）：当函数需要修改指针指向的内容，但不改变指针本身时使用。

二、二级指针（指向指针的指针）

1. 定义与本质

• 二级指针存储的是一级指针的地址，用于间接访问或修改一级指针。

• 例如：int** pp = &p; 表示 pp 指向 int* 类型变量 p 的地址。

2. 典型用法

• 修改一级指针本身：让函数能够改变调用者的指针变量（如重新分配内存、指向新对象）。

• 二维数组的模拟：通过二级指针管理动态分配的二维数组。

• 指针数组的管理：例如命令行参数 char* argv[] 的本质是 char**。

链表节点创建

LTNode* LTBuyNode(LTDataType x)
{
	LTNode* newnode = (LTNode*)malloc(sizeof(LTNode));
	if (newnode == NULL)
	{
		perror("malloc fail!");
		exit(1);
	}
	newnode->data = x;//存放节点数据
	newnode->next = newnode->prev = newnode;//存放两个指针（指向前一个&后一个）

	return newnode;
}

双向链表的打印

void LTPrint(LTNode* phead)
{
	LTNode* pcur = phead->next;
   //当pcur回到头节点时终止
	while (pcur != phead)
	{
		printf("%d -> ", pcur->data);
		pcur = pcur->next;
	}
	printf("\n");
}

头插&头删

//头插
void LTPushFront(LTNode* phead, LTDataType x)
{
	assert(phead);

	LTNode* newnode = LTBuyNode(x);
	//phead newnode phead->next
	newnode->next = phead->next;
	newnode->prev = phead;

	phead->next->prev = newnode;
	phead->next = newnode;
}
//只有一个头结点的情况下，双向链表为空
bool LTEmpty(LTNode* phead)
{
	assert(phead);
	return phead->next == phead;
}

//头删
void LTPopFront(LTNode* phead)
{
	assert(!LTEmpty(phead));
	LTNode* del = phead->next;//暂存，防止后续访问不到
	//phead del del->next
	del->next->prev = phead;
	phead->next = del->next;

	free(del);
	del = NULL;
}

尾插&尾删

//尾插
void LTPushBack(LTNode* phead, LTDataType x)
{
	assert(phead);

	LTNode* newnode = LTBuyNode(x);
	//phead  phead->prev(尾结点) newnode
	newnode->prev = phead->prev;
	newnode->next = phead;

	phead->prev->next = newnode;
	phead->prev = newnode;
}

//尾删
void LTPopBack(LTNode* phead)
{
	assert(!LTEmpty(phead));
	LTNode* del = phead->prev;
	//phead del->prev del
	del->prev->next = phead;
	phead->prev = del->prev;

	free(del);
	del = NULL;
}

查找

LTNode* LTFind(LTNode* phead, LTDataType x)
{
	assert(phead);
	LTNode* pcur = phead->next;
	while (pcur != phead)
	{
		if (pcur->data == x)
		{
			return pcur;
		}
		pcur = pcur->next;
	}
	//没找到
	return NULL;
}

某一位置pos的插入&删除

//在pos位置之后插⼊数据
void LTInsert(LTNode* pos, LTDataType x)
{
	assert(pos);
	LTNode* newnode = LTBuyNode(x);
	//pos newnode pos->next
	newnode->next = pos->next;
	newnode->prev = pos;

	pos->next->prev = newnode;
	pos->next = newnode;
}
//删除pos位置的结点
void LTErase(LTNode* pos)
{
	assert(pos);
	//pos->prev pos pos->next
	pos->next->prev = pos->prev;
	pos->prev->next = pos->next;

	free(pos);
	pos = NULL;
}

销毁双向链表

void LTDesTroy(LTNode* phead)
{
	LTNode* pcur = phead->next;
	while (pcur != phead)
	{
		LTNode* next = pcur->next;
		free(pcur);
		pcur = next;
	}
	free(phead);
	phead = NULL;
}

典型应用

1. 操作系统内存管理

• 空闲内存块管理：
  操作系统通过双向链表维护空闲内存块，方便快速查找、分配和释放内存。例如，当需要分配内存时，可从链表中找到合适大小的块；释放时，可将空闲块插入链表并合并相邻块。

• 进程调度队列：
  进程控制块（PCB）通过双向链表组织成就绪队列、等待队列等，便于调度器快速调整进程顺序（如优先级调度时插入高优先级进程）。

2. 浏览器历史记录

• 前进 / 后退功能：
  浏览器用双向链表存储访问过的 URL，用户点击 “后退” 时沿前驱指针回溯，点击 “前进” 时沿后继指针跳转，时间复杂度为 O (1)。

三、栈

栈（Stack）是一种后进先出（LIFO）的线性表，只允许在一端进行插入和删除操作。我们可以使用顺序结构来实现栈

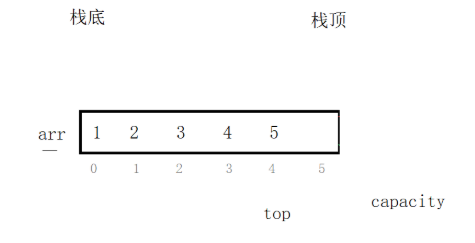
特点

•有明确的的“栈顶”

•插入和删除都在栈顶完成

•逻辑结构是线性的，但在物理存储上可以不连续

栈的底层用数组来实现

头文件

//定义栈的结构
typedef int STDataType;
typedef struct Stack
{
	STDataType* arr;
	int top;     //指向栈顶的位置
	int capacity;//栈的容量
}ST;

//初始化
void StackInit(ST* ps);
//销毁
void StackDestroy(ST* ps);

//入栈---栈顶
void StackPush(ST* ps, STDataType x);
//出栈——栈顶
void StackPop(ST* ps);
//取栈顶元素
STDataType StackTop(ST* ps);

//获取栈中有效元素个数
int StackSize(ST* ps);
//栈是否为空
bool StackEmpty(ST* ps);

典型操作

初始化

void StackInit(ST* ps)
{
	ps->arr = NULL;
	ps->top = ps->capacity = 0;
}

销毁

void StackDestroy(ST* ps)
{
	if (ps->arr)
		free(ps->arr);
	ps->arr = NULL;
	ps->top = ps->capacity = 0;
}

入栈

//入栈---栈顶
void StackPush(ST* ps, STDataType x)
{
	assert(ps);
	if (ps->top == ps->capacity)
	{
		//增容
		int newCapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
		STDataType* tmp = (STDataType*)realloc(ps->arr, newCapacity * sizeof(STDataType));
		if (tmp == NULL)
		{
			perror("realloc fail!");
			exit(1);
		}
		ps->arr = tmp;
		ps->capacity = newCapacity;
	}
	ps->arr[ps->top++] = x;
}

栈的判空

bool StackEmpty(ST* ps)
{
	assert(ps);
	return ps->top == 0;
}

出栈

//出栈——栈顶
void StackPop(ST* ps)
{
	assert(!StackEmpty(ps));
	--ps->top;
}

取栈顶元素

STDataType StackTop(ST* ps)
{
	assert(!StackEmpty(ps));
	return ps->arr[ps->top - 1];
}

获取栈中有效元素个数

int StackSize(ST* ps)
{
	return ps->top;
}
/*
入栈操作：每添加一个元素，top 自增 1。
出栈操作：每移除一个元素，top 自减 1。
空栈状态：top 始终为 0。*/

典型应用：

1.括号匹配与语法检查

•判断表达式中的括号是否配对正确——遇到左括号入栈，遇到右括号弹出栈并匹配

•常用于编译器或代码编辑器的语法检查

2.表达式求值（后缀表达式/中缀转后缀）

•栈是后缀表达式（逆波兰表达式）求值的核心结构

•也用于中缀表达式（人类习惯的表达式）转为后缀表达式

3.递归的实现

•每次递归调用会压入栈中保存状态

•实际上，递归本质就是用函数调用，系统用调用栈来保存中间状态

四、队列

队列（Queue）是一种先进先出（FIFO）的线性表，只允许在一段插入（队尾）,另一端删除（队头）。

特点：

1.数据按顺序排列，有明确的前后关系

2.每个元素只有唯一的前驱和后继（除了第一个和最后一个）

3.插入和删除位置被严格限制，插入只能在尾，删除只能在头

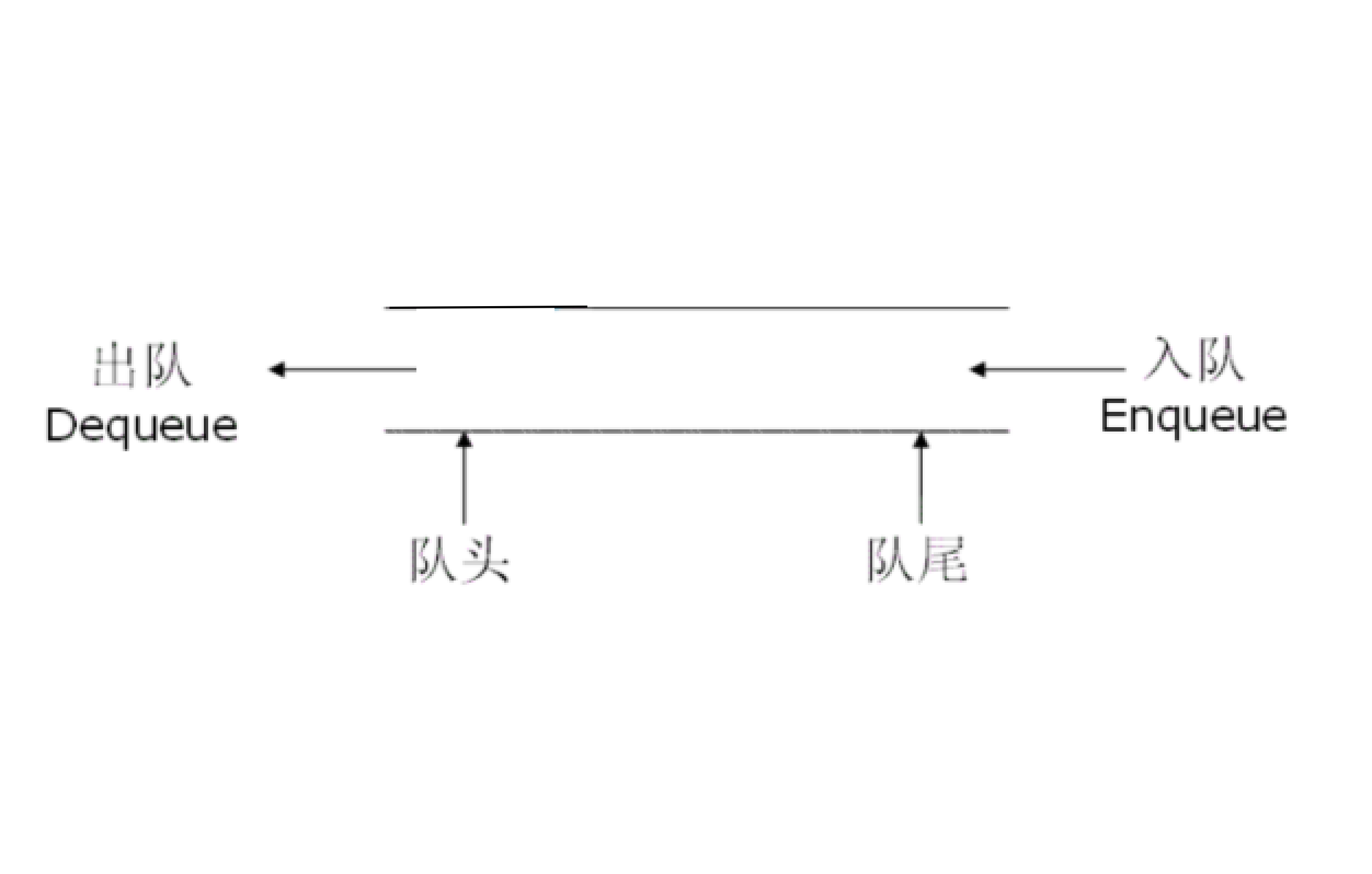
头文件

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

typedef int QDataType;
//队列结点的结构
typedef struct QueueNode
{
	QDataType data;
	struct QueueNode* next;
}QueueNode;
//队列的结构
typedef struct Queue
{
	QueueNode* phead;
	QueueNode* ptail;
	//int size; //队列中有效数据个数
}Queue;

//初始化
void QueueInit(Queue* pq);
//销毁队列
void QueueDestroy(Queue* pq);

//入队——队尾
void QueuePush(Queue* pq, QDataType x);

//出队——队头
void QueuePop(Queue* pq);
//队列判空
bool QueueEmpty(Queue* pq);
//队列有效元素个数
int QueueSize(Queue* pq);

//取队头数据
QDataType QueueFront(Queue* pq);
//取队尾数据
QDataType QueueBack(Queue* pq);

典型操作

初始化

void QueueInit(Queue* pq)
{
	assert(pq);
	pq->phead = pq->ptail = NULL;
	//pq->size = 0;
}

销毁队列

void QueueDestroy(Queue* pq)
{
	assert(pq);
	QueueNode* pcur = pq->phead;
	while(pcur)
	{
		QueueNode* next = pcur->next;
		free(pcur);
		pcur = next;
	}
	pq->phead = pq->ptail = NULL;
	//pq->size = 0;
}

队列判空

bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->phead == NULL;
}

入队——队尾

void QueuePush(Queue* pq, QDataType x)
{
	assert(pq);
	QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		exit(1);
	}
	newnode->data = x;
	newnode->next = NULL;
	//队列为空
	if (pq->phead == NULL)
	{
		pq->phead = pq->ptail = newnode;
	}
	else {
		//队列非空
		pq->ptail->next = newnode;
		pq->ptail = pq->ptail->next;
	}
	//pq->size++;
}

出队——队头

void QueuePop(Queue* pq)
{
	assert(!QueueEmpty(pq));
	//只有一个节点，phead和ptail都套置为空
	if (pq->phead == pq->ptail)
	{
		free(pq->phead);
		pq->phead = pq->ptail = NULL;
	}
	else {
		QueueNode* next = pq->phead->next;
		free(pq->phead);
		pq->phead = next;
	}
	//pq->size--;
}

取队头/队尾数据

//取队头数据
QDataType QueueFront(Queue* pq)
{
	assert(!QueueEmpty(pq));
	return pq->phead->data;
}
//取队尾数据
QDataType QueueBack(Queue* pq)
{
	assert(!QueueEmpty(pq));
	return pq->ptail->data;
}

获取队列有效元素个数

int QueueSize(Queue* pq)
{
	assert(pq);
	//第一种方式：遍历链表——适用于不会频繁调用队列有效数据个数的场景
	QueueNode* pcur = pq->phead;
	int size = 0;
	while (pcur)
	{
		size++;
		pcur = pcur->next;
	}
	return size;
	 
	//第二种方式：遍历链表——适用于频繁调用队列有效数据个数的场景
	//return pq->size;
}

典型应用

1.任务调度、打印队列

操作系统或程序处理任务时，往往按照“先到先处理”的原则

2.进程/线程排队调度

操作系统为多个进程/线程排队时，用队列按顺序调度执行

3.广度优先搜索（BFS）

图论中搜索最短路径问题，使用队列实现层层推进