编译原理 —— DFA的化简

DFA 的化简

任何正规语言都有一个唯一的状态数目最少的DFA

DFA M的化简是指：寻找一个状态数比M少的DFA M’，使得L(M)=L(M’)

有穷自动机的多余状态：从自动机的开始状态出发，任何可识别的输入串也不能到达的状态

化简了的DFA M’ 满足两个条件：

• 没有多余状态 ；
• 没有两个状态是等价的。

---

求解步骤

① 将DFA M的状态集Q分划成两个子集：终态集和非终态集；

② 对每个子集G，如果面对某个输入符号得到的后继状态不属于同一个子集，则将G进一步划分；

③ 重复②直到不再产生新划分；

④ 在每个子集中选一个状态作代表，消去其他状态，得到最少状态的等价DFA M’。

---

示例1

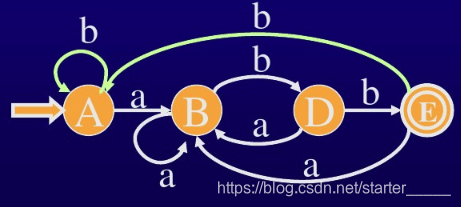
将下图的 DFA 最小化

解：根据规则 ① ，将DFA M的状态集Q分划成两个子集

• ∏ =（{A,B,C,D}，{E}）

根据规则 ② ，因为{A,B,C,D}a={B}⊆{A,B,C,D}\{A,B,C,D\}_a=\{B\}⊆\{A,B,C,D\}{A,B,C,D}a​={B}⊆{A,B,C,D}， 而{A,B,C,D}b={C,D,E}⊄{A,B,C,D}\{A,B,C,D\}_b=\{C,D,E\}⊄\{A,B,C,D\}{A,B,C,D}b​={C,D,E}⊄{A,B,C,D}。因为{A,B,C}b⊆{A,B,C,D}\{A,B,C\}_b⊆\{A,B,C,D\}{A,B,C}b​⊆{A,B,C,D}，{D}b⊆{E}\{D\}_b⊆\{E\}{D}b​⊆{E}，故将{A,B,C,D}\{A,B,C,D\}{A,B,C,D} 划分为{A,B,C}\{A,B,C\}{A,B,C}和{D}\{D\}{D}

• ∏ =（{A,B,C}，{D}，{E}）

根据规则 ② ，因为{A,B,C}a={B}⊆{A,B,C}\{A,B,C\}_a=\{B\}⊆\{A,B,C\}{A,B,C}a​={B}⊆{A,B,C}， 而{A,B,C}b={C,D}⊄{A,B,C}⊄{D}\{A,B,C\}_b=\{C,D\}⊄\{A,B,C\}⊄\{D\}{A,B,C}b​={C,D}⊄{A,B,C}⊄{D}。因为{A,C}b⊆{A,B,C}\{A,C\}_b⊆\{A,B,C\}{A,C}b​⊆{A,B,C}，{B}b⊆{D}\{B\}_b⊆\{D\}{B}b​⊆{D}，故将{A,B,C}\{A,B,C\}{A,B,C} 划分为{A,C}\{A,C\}{A,C}和{B}\{B\}{B}

• ∏ =（{A,C}，{B}，{D}，{E}）

根据规则 ② ，因为{A,C}a={B}⊆{B}⊄{D}⊄{E}\{A,C\}_a=\{B\}⊆\{B\}⊄\{D\}⊄\{E\}{A,C}a​={B}⊆{B}⊄{D}⊄{E}， 而{A,C}b⊆{C}⊆{A,C}\{A,C\}_b⊆\{C\}⊆\{A,C\}{A,C}b​⊆{C}⊆{A,C}。对子集{A,C}\{A,C\}{A,C}，输入后得到的后继状态属于同一个子集{A,C}\{A,C\}{A,C}，故不再进行划分

• ∏ =（{A,C}，{B}，{D}，{E}）

根据规则 ③ ，选择 $A$ 作为 {A，C}\{A，C\}{A，C}的代表，将状态 $C$ 从状态转换图删去，并将原来引向 $C$ 的弧都引至 $A$，这样得到化简后的 DFA M’

• ∏ =（{A}，{B}，{D}，{E}）

---

示例2

将下图的 DFA 最小化

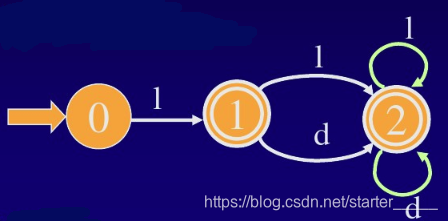
解：

根据规则 ① ，将DFA M的状态集Q分划成两个子集

• ∏ =（{0}，{1,2}）

根据规则 ② ，因为{1,2}l={2}⊆{1,2}\{1,2\}_l=\{2\}⊆\{1,2\}{1,2}l​={2}⊆{1,2}， 而{1,2}d⊆{2}⊆{1,2}\{1,2\}_d⊆\{2\}⊆\{1,2\}{1,2}d​⊆{2}⊆{1,2}。对子集{1,2}\{1,2\}{1,2}，输入后得到的后继状态属于同一个子集{1,2}\{1,2\}{1,2}，故不再进行划分

• ∏ =（{0}，{1,2}）

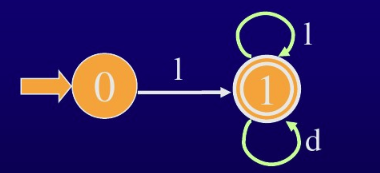
根据规则 ③ ，选择 $1$ 作为 {1，2}\{1，2\}{1，2}的代表，将状态 $2$ 从状态转换图删去，并将原来引向 $2$ 的弧都引至 $1$，这样得到化简后的 DFA M’

• ∏ =（{0}，{1}）