二分查找介绍

1. 二分查找思路介绍

二分查找也叫折半查找，根据名字可知一次解决一半数据。对于一个有序数组a[]，要查找目标元素n，l为其下标0，r为最大即最右边的下标，mid为中间下标。mid = (l+r+1)/2，若arr[mid]小于n，则令l = mid，若arr[mid] 大于n，令r = mid - 1，若相等，令l = mid，并退出查找，否则一直求mid直到l = r，退出查找。如下图

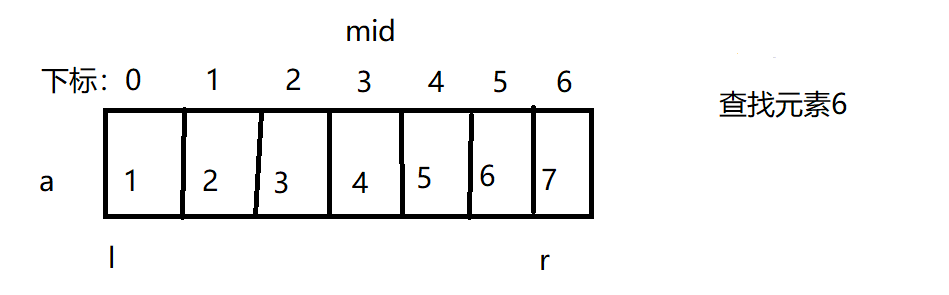
图一

由于a[mid] < 6,令l = mid，继续求mid

图二

此时a[mid] == 6，令l = mid，并不再执行

图三

找出目标元素所在下标为l

代码实现

#include<iostream>
using namespace std;
int main()
{
    int arr[9]; //arr是一个有序数组
    for (int i = 0; i < 9; i++)
    {
        cin >> arr[i];
    }
    int n;
    cin >> n; //n为目标元素
    int l = 0, r, mid;
    r = sizeof(arr) / sizeof(int) - 1;
    while (l != r)
    {
        mid = (l + r + 1) / 2;
        if (arr[mid] < n)
        {
            l = mid;
        }
        else if (arr[mid] == n)
        {
            l = mid;
            break;
        }
        else
        {
            r = mid - 1;
        }
    }
    if (arr[l] == n) cout << l << endl; //输出目标元素的下标l
    else cout << "找不到目标元素";
    return 0;
}

2.为什么写成mid = (l+r+1)/2，而非mid = (l+r)/2

如图二，此时mid对应的下标为5，若目标元素为19，不在数组中，此时l = mid = 5，r = 6，若按照mid = (l+r)/2来求，结果仍为mid = 5，会陷入死循环。

3.令l = mid，而不是l = mid + 1

此时l = r，这个循环中查找已经结束，虽然l对应的值是7，但在下一次循环中才能找出，然而因为l=r，所以退出循环，不能返回l对应的下标。