选择第K大元素（快排、快选以及k-选取比较）

最新推荐文章于 2024-04-03 08:22:16 发布

原创

最新推荐文章于 2024-04-03 08:22:16 发布 · 897 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #算法

本文通过实验对比了在不同规模数据中，使用快速排序、K-选取和快速选择算法寻找第K大元素的性能。尽管K-选取算法在理论上更为稳定，但实测中快速选择的效率更高，尤其是在大规模无序数据中。关键代码展示了三种算法的实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

选择第K大元素（快排、快选以及k-选取比较）

问题：编写一段程序，随机生成10^4, 10^5, 10^6个随机数，并分别在这三者中，分别使用快排和linearSelect()方法，选择出第100大的数字(需给出)，并给出三者的运行时间（可以表格形式给出），给出linearSelect()关键代码并解释。

先看运行结果

N	10000	100000	1000000
T(quicksort) /ms	0.9935	14.0503	151.739
T(K-Select)/ms	0.5436	6.4808	52.8341
T(qucikSelect)/ms	0.0083	0.2679	6.8944

基础测试
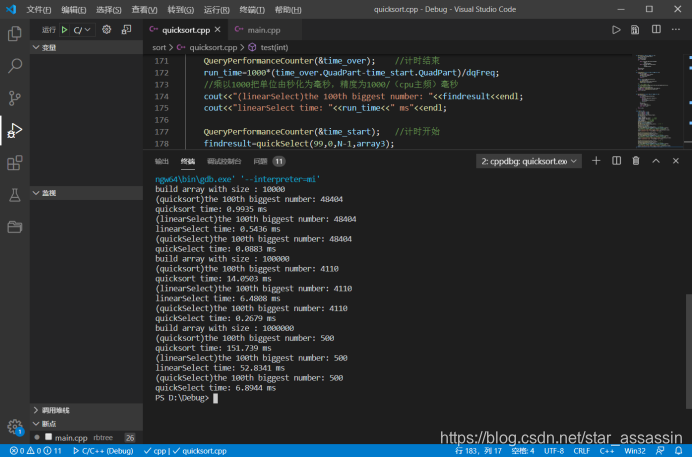
按照书中所给的快排、快选以及K-选取算法分别写出函数检测运行结果以及时间
发现不出所料的直接快排算法会慢很多，但预想更稳定的K-选取算法的耗时比预期设想要大，而相对不太稳定的快选算法却是三者之中最快的，为了避免偶然性，又重复做了多组实验，并将N的范围扩大到100~1000000，实验结果如下：
扩展测试
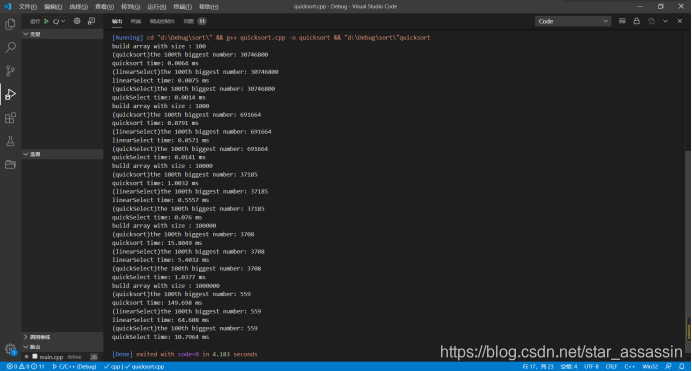
但是之前查过资料，k-选取方法应该是线性的，quickselect算法平均情况是线性的，但最坏的情况下，也会达到O（n2），但在实验中，我却发现quickselect算法的性能元好于k-选取算法。
同时，我也注意到K-选取耗时和quickselect耗时也都比较符合线性递增的规律。所以，二者在数据集都比较杂乱随机的情况下，线性时间复杂度是符合理论推导的。
但为什么更加稳定的k-选取算法会比quickselect慢那么多呢？二者同是运用减而治之，逐步逼近的策略啊！
再次观察代码，我们不难发现，在k-选取算法中，它有以下几个缺点：

对于数组中的几乎所有元素都有分类排序，虽然是每一小分组内的排序，但是确实是会消耗更多的时间，就算是用快排实现这样的组内排序也是耗时颇多；O（n）耗时
每组分好后，我们同样需要再对分出组的中位数再次这样的排序，当然，这里的耗时会相对小很多
找出中位数后，我们又需要根据中位数的位置再次分类取值，这里有会是O（n）的时间
之后才能根据位置进行“减”

综上：此算法虽然稳定，但属实繁琐
而在快速选取算法中，我们始终只分大组，循环不会层层嵌套式深入，遍历一遍之后就可以迅速分组，从而加快寻找的步伐！（但确实如果运气不好，分组太不均匀的话，着实会变成O（n2）的复杂度）。

总结：数据无序度高，且数据量庞大的情况下，个人认为，要实现选择第k大的元素，快选的综合实用效率更好一些。

话不多说，上关键代码：

快排

void quickSort(int low,int high,int* a){
   
   
    if(high-low<1)return;
    if(high-low==1){
   
   
        if(a[low]>a[high])swap(a[low],a[high]);
        return;
    }
    int middle=partition(low,high,a);
    if(middle> low)    quickSort(low,middle-1,a);
    if(middle< high)    quickSort(middle