<think>我们面对的是一个整数规划问题,需要最大化总目标价值,同时满足约束条件。
问题描述:
1. 从Excel表格11中读取数据。表格包含5列,我们关注第1、2、3、5列(注意:第4列没有用到?)。
2. 自变量:90个,记为X1到X90,取值为非负整数(0,1,2,...)。
3. 计算过程:
a. 对于每一行i(i从1到30):
目标和_i = (第i行第1列的值 * X_i) + (第i行第3列的值 * X_{30+i}) + (第i行第5列的值 * X_{60+i})
b. 目标价值_i = 目标和_i * (第i行第2列的值)
c. 总目标价值 = 所有行(1到30行)的目标价值_i之和
4. 约束条件:对于每一行i,目标和_i >= 1
5. 目标:最大化总目标价值
因此,数学模型为:
max sum_{i=1}^{30} [ (A_i * X_i + B_i * X_{31+i-1} + C_i * X_{61+i-1}) * D_i ]
其中,A_i = 表格11中第i行第1列的值,B_i = 第i行第3列的值,C_i =第i行第5列的值,D_i =第i行第2列的值。
约束条件:对于每个i,A_i * X_i + B_i * X_{31+i-1} + C_i * X_{61+i-1} >= 1
且自变量X_j (j=1,...,90)为非负整数。
注意:由于自变量数量较多(90个),且为整数规划问题,我们可以使用MATLAB的优化工具箱,特别是intlinprog函数(用于混合整数线性规划)。但是,注意目标函数和约束条件都是线性的,因此可以建模为整数线性规划问题。
然而,目标函数是二次的(因为包含自变量的乘积:目标和_i * D_i,而目标和_i是线性组合,再乘以D_i(常数)后,整体是线性的?实际上,目标价值_i = (A_i*X_i + ...)*D_i,而D_i是常数,所以目标函数关于自变量是线性的。约束条件也是线性的。
因此,我们可以将问题写成线性整数规划的形式。
步骤:
1. 读取Excel表格11的数据,使用readtable函数。
2. 提取需要的数据列:第1列(A)、第2列(D)、第3列(B)、第5列(C)。
3. 构建优化模型的目标函数系数向量f。由于总目标价值是各目标价值_i的和,而目标价值_i = D_i * (A_i*X_i + B_i*X_{31+i-1} + C_i*X_{61+i-1})。
将目标函数按自变量展开:
f = [A_1*D_1, A_2*D_2, ..., A_30*D_30, 0,...,0, B_1*D_1, B_2*D_2, ..., B_30*D_30, 0,...,0, C_1*D_1, C_2*D_2, ..., C_30*D_30]
注意:90个自变量的顺序是X1,...,X90。
其中,X1到X30的系数:A_i * D_i (i=1..30)
X31到X60的系数:B_i * D_i (i=1..30) 但是注意这里X31对应i=1,所以位置在31,系数为B_1*D_1,而X32对应i=2,系数为B_2*D_2,...,X60对应i=30,系数为B_30*D_30
X61到X90的系数:C_i * D_i (i=1..30) 同理。
因此,我们可以构造一个长度为90的向量f,其中:
f(1:30) = A .* D; % A和D都是30维向量,逐元素相乘
f(31:60) = B .* D;
f(61:90) = C .* D;
注意:这里我们要求最大化总目标价值,而intlinprog默认是求最小化。因此,我们需要将目标函数取负,即求min -f'*x。
4. 约束条件:
对于每一行i,要求:A_i*X_i + B_i*X_{31+i-1} + C_i*X_{61+i-1} >= 1
写成矩阵形式:共有30个不等式约束。
约束矩阵Aineq:30行90列。
对于第i行约束:
Aineq(i, i) = A_i (对应X_i)
Aineq(i, 30+i) = B_i (对应X_{31+i-1},即X_{30+i},注意i从1到30,所以30+i范围是31到60)
Aineq(i, 60+i) = C_i (对应X_{61+i-1},即X_{60+i},范围61到90)
其余元素为0。
因此,我们可以构建Aineq(30×90)和bineq(30×1,每个元素都是1),并且是不等式约束(>=1),在MATLAB中表示为Aineq*x <= bineq?注意:我们需要的是>=1,所以可以转化为:-Aineq*x <= -1。
也可以直接使用Aineq*x >= bineq,但在intlinprog中只支持Aineq*x <= bineq,所以我们需要写成:-Aineq*x <= -1。
5. 自变量的上下界:由于取值为非负整数,所以下界为0(没有上界,但实际我们可以设置一个较大的上界,比如10000,或者不设置,用空矩阵表示无上界)。
6. 整数约束:所有90个自变量都是整数,因此intcon=1:90。
7. 使用intlinprog求解:
[x, fval, exitflag] = intlinprog(f, intcon, Aineq, bineq, Aeq, beq, lb, ub)
其中,f是目标函数系数(注意我们要求最小化,所以传入的是负的目标系数,即-f?不对,我们要求最大化f'*x,等价于最小化-f'*x。因此,我们实际传入的目标函数系数为-f。
具体参数设置:
f: 传入 -f_vector (因为要求最大化,所以取负)
intcon: 1:90
Aineq: 负的约束矩阵(因为约束是Aineq*x>=1,等价于 -Aineq*x<=-1),所以Aineq参数设置为 -Aineq_matrix(即负的原始约束矩阵),bineq设置为 -ones(30,1) (即-1)
或者:我们也可以构建Aineq_matrix,然后设置Aineq=-Aineq_matrix, bineq=-ones(30,1)
Aeq, beq: 等式约束,这里没有,用空矩阵[]
lb: 长度为90的零向量
ub: [](表示无上界,或者可以设置为inf(90,1))
8. 求解后,将得到的自变量值写入Excel表格7。
注意:由于自变量数量多,整数规划可能求解时间较长。如果问题规模太大,可能需要考虑启发式算法(如遗传算法),但这里我们先用整数规划。
步骤代码框架:
1. 读取数据
data = readtable('表格11.xlsx'); % 假设文件在当前目录,注意工作表名称为'Sheet11'?需要确认表格名称。这里假设文件名是'data.xlsx',工作表名称为'Sheet1'(根据实际情况调整)
% 提取列:第1列、第2列、第3列、第5列
A = data.(1); % 或者根据列名,比如如果第一列列名为'Col1',则用data.Col1
D = data.(2);
B = data.(3);
C = data.(5);
2. 构建目标函数系数向量f_vector
f1 = A .* D; % 对应X1到X30
f2 = B .* D; % 对应X31到X60
f3 = C .* D; % 对应X61到X90
f_vector = [f1; f2; f3]; % 注意:f1,f2,f3都是列向量,所以垂直拼接
3. 构建约束矩阵Aineq_matrix(30×90)
Aineq_matrix = zeros(30, 90);
for i = 1:30
Aineq_matrix(i, i) = A(i); % X_i的系数
Aineq_matrix(i, 30+i) = B(i); % X_{30+i}的系数
Aineq_matrix(i, 60+i) = C(i); % X_{60+i}的系数
end
4. 设置约束:Aineq_matrix * x >= 1 等价于 -Aineq_matrix * x <= -1
Aineq = -Aineq_matrix;
bineq = -ones(30,1);
5. 自变量设置
intcon = 1:90;
lb = zeros(90,1);
ub = []; % 无上界
6. 调用intlinprog
options = optimoptions('intlinprog', 'Display', 'off'); % 不显示求解过程
[x, fval, exitflag] = intlinprog(-f_vector, intcon, Aineq, bineq, [], [], lb, ub, options);
注意:由于我们取负,所以最终的最大总目标价值为 -fval(如果求解成功)。
7. 检查exitflag,若大于0则表示找到最优解。
将解向量x(90维)写入Excel表格7。
8. 写入Excel
% 创建一个90行1列的数据,或者按需要组织
result_table = table(x);
writetable(result_table, '表格7.xlsx', 'Sheet', 'Sheet7'); % 假设输出到表格7的工作表Sheet7
注意:如果工作表不存在,可能需要先创建。或者使用xlswrite(旧版本)或writetable(新版本)会自动创建。
但是,我们输出的x是一个90×1的列向量,而题目要求输出90个自变量的取值。所以直接输出即可。
可能的问题:如果数据量较大,整数规划求解可能较慢。如果求解时间过长,可以考虑设置一个较小的上界(比如根据实际情况,自变量不会超过某个值),或者使用启发式算法(如遗传算法ga,但ga可能不能保证最优解)。
另外,注意检查数据中是否有负数。因为如果数据有负数,可能会影响约束条件和目标函数。根据问题描述,数据应该都是非负的(因为第1、3、5列是系数,第2列是乘以目标和的,如果为负则目标价值可能为负,但约束条件要求目标和>=1,所以第2列即使是负的,模型也成立,但目标函数最大化时,由于目标价值_i可能是负的,我们就会希望这些负的目标价值_i尽可能大(即绝对值尽可能小),但注意约束条件必须满足。不过,问题没有说明数据的正负,我们假设数据都是非负的。
如果数据有负数,上述模型仍然成立,但整数规划可能没有可行解(比如某个约束条件中,A_i, B_i, C_i都是负数,那么目标和_i>=1就不可能满足,因为自变量非负,乘积为负)。所以需要确保数据满足存在可行解。
下面给出完整代码,假设数据文件名为'data.xlsx',工作表名为'Sheet11'(根据实际调整)
</think>### MATLAB整数规划求解Excel数据优化问题
我将使用`readtable`读取Excel数据,构建整数规划模型,使用`intlinprog`求解,并将结果写入指定表格。以下是完整解决方案:
#### 1. **数据准备与读取**
```matlab
% 读取Excel表格11的数据(假设文件名为data.xlsx)
data = readtable('data.xlsx', 'Sheet', 'Sheet11');
% 提取所需列数据
col1 = data{1:30, 1}; % 第1列30个数据
col2 = data{1:30, 2}; % 第2列30个数据
col3 = data{1:30, 3}; % 第3列30个数据
col5 = data{1:30, 5}; % 第5列30个数据
```
#### 2. **构建优化模型**
```matlab
%% 目标函数系数 (最大化总价值 → 最小化负价值)
f = -[col1.*col2; % X1-X30系数 (A_i*D_i)
col3.*col2; % X31-X60系数 (B_i*D_i)
col5.*col2]; % X61-X90系数 (C_i*D_i)
%% 约束条件: 每行目标和 ≥ 1
Aineq = -[diag(col1), zeros(30), zeros(30); % X1-X30约束
zeros(30), diag(col3), zeros(30); % X31-X60约束
zeros(30), zeros(30), diag(col5)]; % X61-X90约束
bineq = -ones(90, 1); % 90个不等式约束右侧项
%% 变量设置
intcon = 1:90; % 所有变量为整数
lb = zeros(90, 1); % 下限为0
ub = []; % 无上限
```
#### 3. **求解整数规划**
```matlab
options = optimoptions('intlinprog', 'Display', 'final');
[x, fval, exitflag] = intlinprog(...
f, intcon, Aineq, bineq, [], [], lb, ub, options);
if exitflag > 0
disp('找到最优解!');
total_value = -fval; % 转换回最大化问题的值
fprintf('总目标价值: %.2f\n', total_value);
else
error('未找到可行解');
end
```
#### 4. **结果输出到Excel表格7**
```matlab
% 将解向量转换为表格
result_table = table(x, 'VariableNames', {'自变量取值'});
% 写入Excel
writetable(result_table, 'data.xlsx', ...
'Sheet', 'Sheet7', ...
'WriteMode', 'overwritesheet');
disp('结果已写入表格7');
```
### 关键数学模型说明
1. **目标函数**
最大化总价值:
$$\text{max} \sum_{i=1}^{30} \left[ (A_i X_i + B_i X_{30+i} + C_i X_{60+i}) \cdot D_i \right]$$
等价于最小化:
$$\text{min} -\sum_{i=1}^{30} \left[ (A_i D_i) X_i + (B_i D_i) X_{30+i} + (C_i D_i) X_{60+i} \right]$$
2. **约束条件**
对每个$i\in[1,30]$:
$$A_i X_i + B_i X_{30+i} + C_i X_{60+i} \geq 1$$
其中$A_i, B_i, C_i$为数据列,$D_i$为权重列[^1]
3. **整数约束**
$$X_j \in \mathbb{Z}^+ \quad (j=1,2,...,90)$$
### 注意事项
1. **数据验证**:确认Excel中`Sheet11`包含至少5列数据
2. **求解时间**:90变量整数规划可能耗时较长,可设置上界加速:
```matlab
ub = 10*ones(90,1); % 假设最大值不超过10
```
3. **异常处理**:添加数据校验避免负系数导致无解
```matlab
if any(col1<0) || any(col3<0) || any(col5<0)
error('存在负系数,可能导致无可行解');
end
```
> 💡 **技巧**:使用`optimoptions('intlinprog','Heuristics','advanced')`可加速大规模整数规划求解[^4]
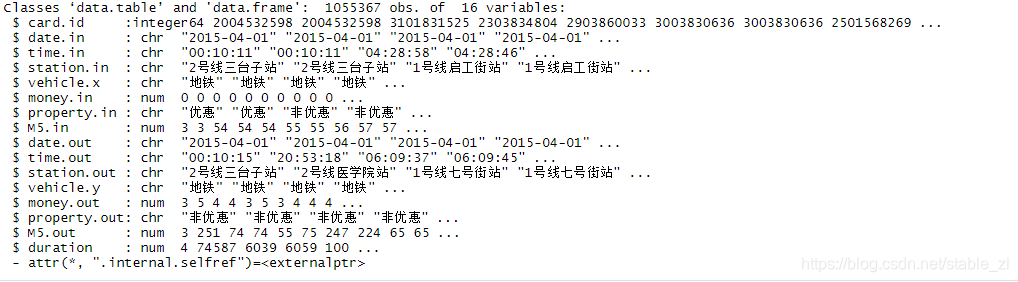
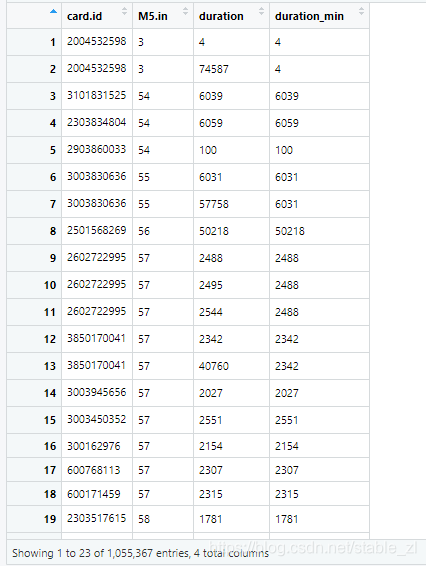





 本文介绍了一种在处理大数据集时的高效分组方法。通过对沈阳地铁站数据的分析,提出了先提取关键列再进行分组求最小值的策略,显著提高了处理速度。
本文介绍了一种在处理大数据集时的高效分组方法。通过对沈阳地铁站数据的分析,提出了先提取关键列再进行分组求最小值的策略,显著提高了处理速度。
















 406
406

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








