【多模态非刚性Demon算法图像配准】非刚性 2D 和 3D 图像配准，使用 Demon流算法，扩展了模态转换研究（Matlab代码实现）

  💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

 ⛳️赠与读者

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

---

 ⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。当哲学课上老师问你什么是科学，什么是电的时候，不要觉得这些问题搞笑。哲学是科学之母，哲学就是追究终极问题，寻找那些不言自明只有小孩子会问的但是你却回答不出来的问题。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能让人胸中升起一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它居然给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

     或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

【多模态非刚性demon算法图像配准】非刚性 2D 和 3D 图像配准，使用 demon流算法，扩展了模态转换研究

多模态非刚性 demon 算法图像配准，非刚性 2D 和 3D 图像配准，使用 demon（流体）算法，扩展了模态转换。
本文讲解一种快速非刚性流体，如两个2D或3D图像之间的注册。通过一种功能，该功能将一种图像模态转换为看起来像第二种图像模态，也支持不同（MRI）模态之间的配准。

一、引言

图像配准是图像处理和分析中的一个关键步骤，特别是在医学成像领域。非刚性图像配准能够处理形状和解剖结构的变化，这在处理不同时间点的图像或不同模态的图像时尤为重要。Demon（流体）算法是一种有效的非刚性配准方法，特别适用于处理复杂变形。本文将介绍一种基于Demon算法的多模态非刚性图像配准方法，该方法不仅适用于2D图像，还扩展到了3D图像，并具备模态转换的能力。

二、背景知识

1. Demon算法：Demon算法是一种基于物理模型的非刚性配准方法，它模拟了流体在力场中的运动，从而实现图像的变形。该算法通过计算目标图像和参考图像之间的梯度差异来驱动变形，使得变形后的图像与目标图像更加接近。

2. 多模态图像配准：多模态图像配准是指将来自不同成像模态的图像进行对齐。由于不同模态的图像可能具有不同的灰度值范围和对比度，因此多模态配准通常比单模态配准更具挑战性。

三、方法

1. 预处理：在进行配准之前，需要对图像进行预处理，包括去噪、增强对比度等。对于多模态图像，还需要进行模态转换，以使不同模态的图像在灰度值上更加接近。

2. Demon算法实现：

   • 计算梯度：首先计算目标图像和参考图像的梯度场。
   • 计算力场：根据梯度场计算力场，该力场将驱动图像变形。
   • 更新变形场：使用力场更新变形场，使图像逐渐变形为目标图像的形状。
   • 迭代：重复上述步骤，直到达到预定的迭代次数或满足收敛条件。

3. 模态转换：为了处理多模态图像配准中的灰度值不匹配问题，本文提出了一种模态转换方法。该方法利用机器学习算法（如深度学习模型）来学习不同模态图像之间的映射关系，从而实现模态转换。

四、实验结果

在实验中，我们使用了来自不同成像模态的2D和3D图像数据集进行配准。实验结果表明，该方法能够有效地实现多模态非刚性图像配准，并且模态转换方法显著提高了配准的准确性。特别是在处理具有复杂解剖结构和显著灰度值差异的图像时，该方法表现出色。

五、结论

本文提出了一种基于Demon算法的多模态非刚性图像配准方法，并扩展了模态转换的研究。该方法不仅适用于2D图像，还成功应用于3D图像配准。实验结果表明，该方法在处理多模态图像配准时具有显著的优势，并且模态转换方法进一步提高了配准的准确性。未来，我们将继续研究更高效的模态转换方法和更鲁棒的配准算法，以应对更加复杂和多样化的图像配准任务。

📚2 运行结果

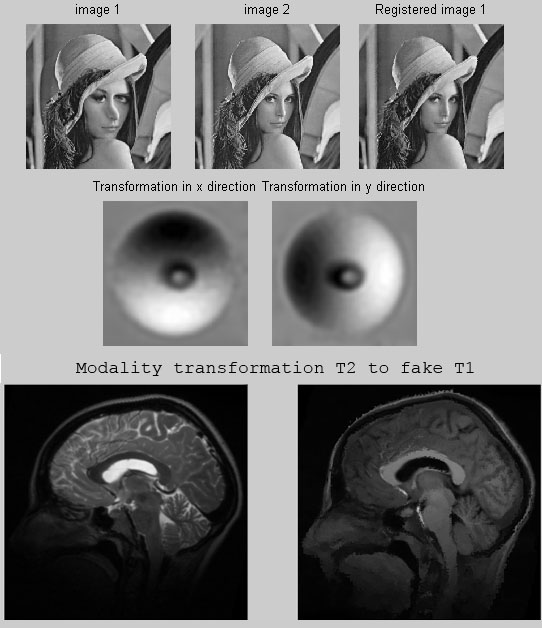
部分代码：

% Clean
clc; clear all; close all;

% Compile the mex files
compile_c_files

% Read two images
I1=im2double(imread('images/lenag1.png'));  
I2=im2double(imread('images/lenag2.png')); 

% Set static and moving image
S=I2; M=I1;

% Alpha (noise) constant
alpha=2.5;

% Velocity field smoothing kernel
Hsmooth=fspecial('gaussian',[60 60],10);

% The transformation fields
Tx=zeros(size(M)); Ty=zeros(size(M));

[Sy,Sx] = gradient(S);
for itt=1:200
        % Difference image between moving and static image
        Idiff=M-S;

        % Default demon force, (Thirion 1998)
        %Ux = -(Idiff.*Sx)./((Sx.^2+Sy.^2)+Idiff.^2);
        %Uy = -(Idiff.*Sy)./((Sx.^2+Sy.^2)+Idiff.^2);

        % Extended demon force. With forces from the gradients from both
        % moving as static image. (Cachier 1999, He Wang 2005)
        [My,Mx] = gradient(M);
        Ux = -Idiff.*  ((Sx./((Sx.^2+Sy.^2)+alpha^2*Idiff.^2))+(Mx./((Mx.^2+My.^2)+alpha^2*Idiff.^2)));
        Uy = -Idiff.*  ((Sy./((Sx.^2+Sy.^2)+alpha^2*Idiff.^2))+(My./((Mx.^2+My.^2)+alpha^2*Idiff.^2)));
 
        % When divided by zero
        Ux(isnan(Ux))=0; Uy(isnan(Uy))=0;

        % Smooth the transformation field
        Uxs=3*imfilter(Ux,Hsmooth);
        Uys=3*imfilter(Uy,Hsmooth);

        % Add the new transformation field to the total transformation field.
        Tx=Tx+Uxs;
        Ty=Ty+Uys;
        M=movepixels(I1,Tx,Ty); 
end

subplot(1,3,1), imshow(I1,[]); title('image 1');
subplot(1,3,2), imshow(I2,[]); title('image 2');
subplot(1,3,3), imshow(M,[]); title('Registered image 1');

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。(文章内容仅供参考，具体效果以运行结果为准)

[1]郝培博,陈震,江少锋,等.基于Demons算法的多模态医学图像非刚性配准研究[J].生物医学工程学杂志, 2014, 31(1):5.

[2]胡永祥.基于互信息的多模态医学图像非刚性配准研究[D].中南大学[2024-11-19].DOI:CNKI:CDMD:1.1012.474420.

[3]石跃祥,陈才.基于最优Atlas多模态图像的非刚性配准分割算法[J].光学学报, 2019, 39(4):11.

🌈4 Matlab代码实现

资料获取，更多粉丝福利，MATLAB|Simulink|Python资源获取