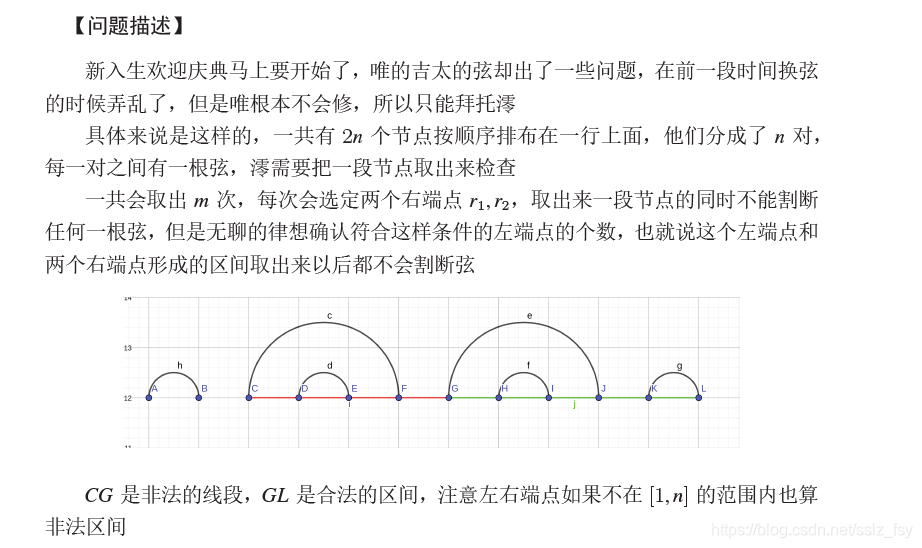
考虑一个 rrr 哪些 lll 可以作为它的答案
就是不存在一个弦的左括号在区间内右括号在区间外或者左括号在区间外右括号在区间内
开始想的是打一个差分标记然后判断是不是为 0,发现凉了
因为存在这种情况:一个右括号在里面左括号在外面,左括号在里面右括号在外面
回到原来的问题,给定一个区间,问存不存在更这个区间交叉的区间
于是我们可以给每个区间分配一个 valvalval,在 l,rl,rl,r 打上标记,然后求前缀异或和
显然两个都在里面会异或成 0,一个在里面会有 valvalval 的贡献
于是一个合法的区间的异或和为 0,求一个前缀和,就是对 r1r_1r1 统计前面为 r1r_1r1 的个数
这里可以忽略掉 r2r_2r2是因为 sumr2!=sumr1sum_{r_2}!=sum_{r_1}sumr2!=sumr1 的话已经凉了,于是只用考虑 r1r_1r1
离线用桶维护即可
正解:发现可以对每个点求出它作为右端点的极小答案区间
然后可以作为答案的区间就是这些极小区间并起来
有一个 显然 的策略是一个 rrr 跳到它的最小区间的左端点 lll,然后再往左跳一步
如果跳到左括号已经凉了不能继续跳因为跳了一定跨出了一个区间
如果是右括号就可以用上述策略继续跳
于是有一个建图策略是 rrr 向 lll 的前一个连边,显然是一棵树
r1,r2r_1,r_2r1,r2 的 lcalcalca 的深度就是合法的左端点个数
#include<bits/stdc++.h>
#define cs const
using namespace std;
typedef long long ll;
int read(){
int cnt = 0, f = 1; char ch = 0;
while(!isdigit(ch)){ ch = getchar(); if(ch == '-') f = -1; }
while(isdigit(ch)) cnt = cnt*10 + (ch-'0'), ch = getchar();
return cnt * f;
}
cs int N = 2e6 + 5;
int n, m, l[N], r[N], ct;
bool isr[N];
typedef long long ll;
ll d[N], b[N]; int sz;
ll rnd(){ return (rand() | ((ll)rand() << 15)) * (rand() | ((ll)rand() << 15)); }
vector<int> v[N];
#define pb push_back
int ans[N], bin[N];
int main(){
srand(time(0));
freopen("hotchkiss.in","r",stdin);
freopen("hotchkiss.out","w",stdout);
n = read(), m = read();
for(int i = 1; i <= (n << 1); i++){
int x = read();
if(x > i){ l[++ct] = i; r[ct] = x; isr[x] = true; }
}
for(int i = 1; i <= ct; i++){
d[l[i]] = d[r[i]] = rnd();
}
for(int i = 1; i <= (n << 1); i++){
d[i] ^= d[i-1];
}
if(n <= 2e3){
for(int i = 1; i <= m; i++){
int r1 = read(), r2 = read();
if(r1 > r2) swap(r1, r2);
if(!r1){ puts("0"); continue; }
if(!isr[r1] || !isr[r2]){ puts("0"); continue; }
if(d[r1] != d[r2]){ puts("0"); continue; }
int ans = 0;
for(int l = 1; l < r1; l++) if(!isr[l] && d[l - 1] == d[r1]) ++ans;
cout << ans << '\n';
}
}
else{
for(int i = 1; i <= (n << 1); i++) b[++sz] = d[i]; b[++sz] = d[0];
sort(b + 1, b + sz + 1); sz = unique(b + 1, b + sz + 1) - (b + 1);
for(int i = 0; i <= (n << 1); i++) d[i] = lower_bound(b + 1, b + sz + 1, d[i]) - b;
for(int i = 1; i <= m; i++){
int r1 = read(), r2 = read();
if(r1 > r2) swap(r1, r2);
if(!r1){ ans[i] = 0; continue; }
if(!isr[r1] || !isr[r2]){ ans[i] = 0; continue; }
if(d[r1] != d[r2]){ ans[i] = 0; continue; }
v[r1].pb(i);
}
bin[d[0]]++;
for(int i = 1; i <= (n << 1); i++){
for(int j = 0; j < v[i].size(); j++){
int id = v[i][j];
ans[id] = bin[d[i]];
} bin[d[i]]++;
}
for(int i = 1; i <= m; i++) cout << ans[i] << '\n';
}
return 0;
}
#include<bits/stdc++.h>
#define cs const
using namespace std;
typedef long long ll;
int read(){
int cnt = 0, f = 1; char ch = 0;
while(!isdigit(ch)){ ch = getchar(); if(ch == '-') f = -1; }
while(isdigit(ch)) cnt = cnt*10 + (ch-'0'), ch = getchar();
return cnt * f;
}
cs int N = 2e6 + 5;
int n, m, l[N], r[N], p[N];
int sta[N], top;
int fa[N], rt[N], f[N][20], dep[N];
vector<int> v[N];
void dfs(int u, int RT){
rt[u] = RT;
for(int i = 1; i <= 18; i++) f[u][i] = f[f[u][i-1]][i-1];
for(int i = 0; i < v[u].size(); i++){
int t = v[u][i];
dep[t] = dep[u] + 1; f[t][0] = u; dfs(t, RT);
}
}
int lca(int x, int y){
if(dep[x] < dep[y]) swap(x, y);
for(int i = 18; i >= 0; i--) if(dep[f[x][i]] >= dep[y]) x = f[x][i];
if(x == y) return x;
for(int i = 18; i >= 0; i--) if(f[x][i] ^ f[y][i]) x = f[x][i], y = f[y][i];
return f[x][0];
}
int main(){
n = read(), m = read();
for(int i = 1; i <= (n << 1); i++) p[i] = read();
for(int i = 1; i <= (n << 1); i++){
l[i] = min(i, p[i]);
r[i] = max(i, p[i]);
while(top && l[i] <= sta[top]){
int x = sta[top--];
l[i] = min(l[i], l[x]);
r[i] = max(r[i], r[x]);
} sta[++top] = i;
}
memset(fa, -1, sizeof(fa));
memset(rt, -1, sizeof(rt));
for(int i = 1; i <= (n << 1); i++){
if(r[i] == i){
fa[i] = l[i] - 1;
v[fa[i]].push_back(i);
}
}
for(int i = 0; i <= (n << 1); i++){
if(v[i].size() && !(~rt[i])) dep[i] = 1, dfs(i, i);
}
for(int i = 1; i <= m; i++){
int r1 = read(), r2 = read();
if(r1 > r2) swap(r1, r2);
if(!r1){ puts("0"); continue; }
if(!(~rt[r1]) || !(~rt[r2])){ puts("0"); continue; }
if(rt[r1] ^ rt[r2]){ puts("0"); continue; }
cout << dep[lca(r1, r2)] - 1 << '\n';
}
return 0;
}







 本文深入探讨了一种解决区间匹配问题的高效算法。通过利用前缀异或和与极小区间概念,文章提出了一种新颖的策略来判断一个区间是否与另一个区间交叉。此外,文章还介绍了一种基于树状结构的建图策略,用于计算合法左端点的数量。
本文深入探讨了一种解决区间匹配问题的高效算法。通过利用前缀异或和与极小区间概念,文章提出了一种新颖的策略来判断一个区间是否与另一个区间交叉。此外,文章还介绍了一种基于树状结构的建图策略,用于计算合法左端点的数量。

















 330
330












