【DFS】排排坐

排排坐

题目大意：

有n个方块，有一些是黑色，有一些是白色，可以点击一个方块使它和它旁边的方块反转颜色（黑变白，白变黑），问最少要点多少次才能将方块 们 变成目标的方块们，如果不行，输出"Boring"

原题：

题目描述

小B喜欢在蓝心网玩游戏,一天他玩到了这个游戏:他感觉非常好玩…于是他就YY出了一个类似的简易模型…
游戏规则：每次点击一个小朋友，他和他的周围的小朋友都会改变状态（蹲下的变成了站起来的，站起来的变成了蹲下的）
我们将这个抽象成如下图所示的1*N的图.对于一个单元格,黑色表示小朋友是站起来的,反之,蹲下的小朋友是是白色的.Source表示初始状态,Target表示目标状态.

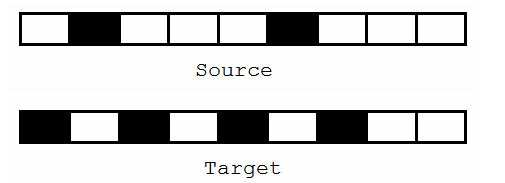
现在小B有点偷懒,希望作为神牛的你帮小B算出初始状态到目标状态的最少点击数.

输入

第一行为N表示小朋友的个数.
第二行是初始状态,有N个数,每个数不是0就是1.(0表示小朋友是蹲下的,1表示小朋友是站起来的)
第三行的结构跟第二行类似,表示目标状态

输出

一个数X,表示初始状态到目标状态的最少点击数。
如果无法到达目标,则请输出"Boring"

输入样例

9
0 1 0 0 0 1 0 0 0 
1 0 1 0 1 0 1 0 0

输出样例

2

只需要点击第二个和第六个点即可。

说明

对于100%的数据，N<=10

解题思路：

枚举每一个方块，看点不点，就是O（$2^{10}$），然后判断，求最小即可

代码：

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
int n,t,ans,a[15],b[15];
void dfs(int dep,int now)
{
	if (dep>n)//已完成
	  {
	  	t=0;//清零
	  	for (int i=1;i<=n;++i)
	  	  if (a[i]!=b[i]) t=1;//有一个不同就不行
	  	if (!t) ans=min(ans,now);//取最小值
	  	return;
	  }
	if (now>=ans) return;
	a[dep-1]=(a[dep-1]+1)%2;//翻
	a[dep]=(a[dep]+1)%2;
	a[dep+1]=(a[dep+1]+1)%2;
	dfs(dep+1,now+1);
	a[dep-1]=(a[dep-1]+1)%2;//返回去
	a[dep]=(a[dep]+1)%2;
	a[dep+1]=(a[dep+1]+1)%2;
	dfs(dep+1,now);
}
int main()
{
	scanf("%d",&n);
	for (int i=1;i<=n;++i)
	  scanf("%d",&a[i]);
	for (int i=1;i<=n;++i)
	  scanf("%d",&b[i]);
	ans=2147483647;
	dfs(1,0);
	printf("%d",ans);//输出
}