集成运放应用分析（后篇） ---单电源运放在使用时的缺陷----同相与反相放大适用场景

一、单电源运放的输出无法到0V是通病还是个例？

这是绝大多数传统单电源运放的“通病”，这里以LM358为例。 

根源在于运放的输出级结构：
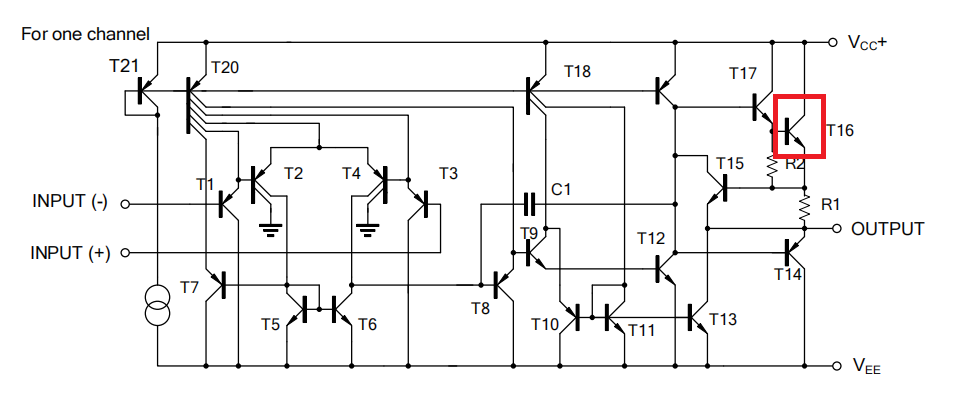
传统运放（如LM358、LM741、TL0xx系列）使用BJT（双极性晶体管） 作为输出级。为了不产生交越失真，输出级通常工作在AB类（甲乙类）。

• 下拉晶体管（NPN或N沟道）：这个管子负责将输出拉低（Sink电流）。

• 上拉晶体管（PNP或P沟道）：这个管子负责将输出拉高（Source电流）。

问题就出在“上拉晶体管”上：
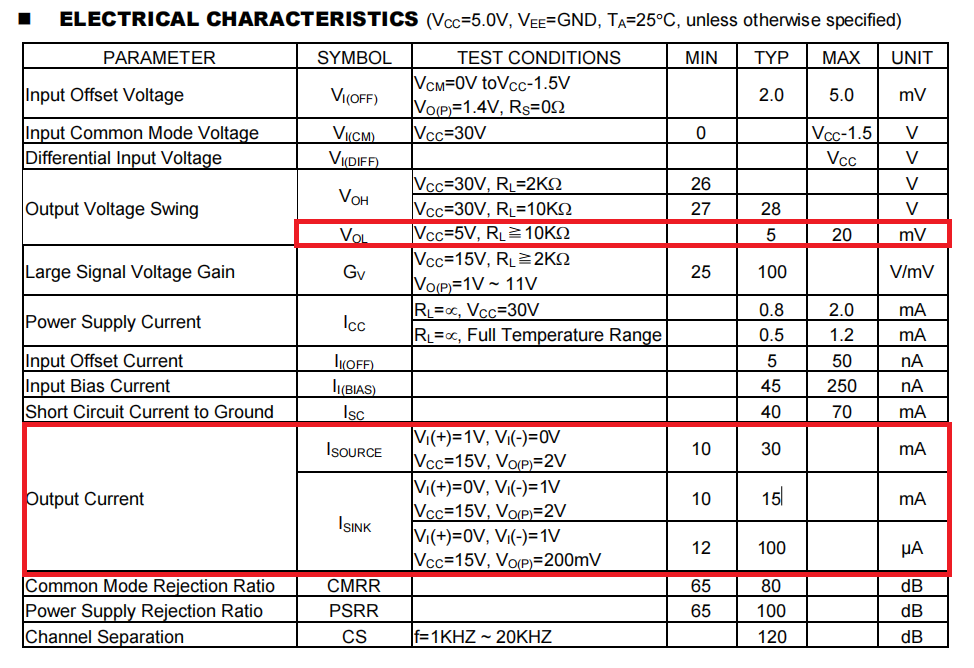
在传统的PNP晶体管输出结构中，即使晶体管完全导通（饱和），它的集电极和发射极之间仍然存在一个小的压降，称为饱和压降（Vce_sat）。这个值通常在几十到几百毫伏之间。

因此，当运放试图输出0V时，下拉晶体管虽然能很好地把输出拉到地电位，但上拉晶体管并未完全关断，仍存在一个微小的导通路径，导致输出无法完全达到0V，而是停留在 Vout_min = Vce_sat 的水平。对于LM358，这个值在数据手册中规定为典型值5mV，最大20mV（在轻负载条件下）。

<