给定n个起点和对应的n个终点，这n条不相交路径的方案数为

最新推荐文章于 2021-04-03 17:47:55 发布

原创最新推荐文章于 2021-04-03 17:47:55 发布 · 456 阅读

1 ·

CC 4.0 BY-SA版权

数论专栏收录该内容

5 篇文章

订阅专栏

本文介绍了一个算法问题，即计算满足特定条件的n×m矩阵的数量。矩阵中的元素必须在0到2之间，且遵循行和列的递增规则。通过使用组合数学原理，文章提供了求解该问题的代码实现，包括阶乘、逆元的快速幂计算以及最终结果的求解。

题目描述
Count the number of n x m matrices A satisfying the following condition modulo (109+7).

Ai, j ∈ {0, 1, 2} for all 1 ≤ i ≤ n, 1 ≤ j ≤ m.
Ai, j ≤ Ai + 1, j for all 1 ≤ i < n, 1 ≤ j ≤ m.
Ai, j ≤ Ai, j + 1 for all 1 ≤ i ≤ n, 1 ≤ j < m.

输入
The input consists of several test cases and is terminated by end-of-file.
Each test case contains two integers n and m.

输出
For each test case, print an integer which denotes the result.

样例输入
复制样例数据
1 2
2 2
1000 1000
样例输出
6
20
540949876

提示

1 ≤ n, m ≤ 103
The number of test cases does not exceed 105.

这张图片是网上到处流传的一张图片定理，虽然我也不懂，但是我可以理解一下
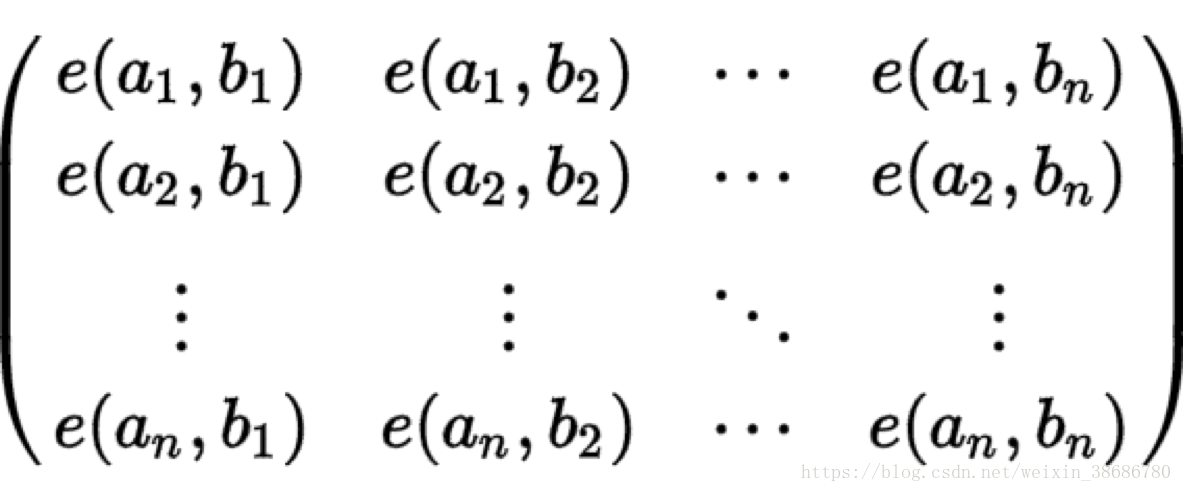
在这里插入图片描述
求以上矩阵的行列式，其中 e(a,b) 是从a到b的方法数，带入求行列式即可得到(a1,a2,…an) 到 (b1,b2,…bn) 的所有不相交路径的种数

考虑01和12的分界线是(n, 0)到(0，m)的两条不相交（可重合）路径，
分界线以及分界线以上的点是一种，分界线下是一种
平移其中一条变成(n-1, -1)到(-1，m-1);

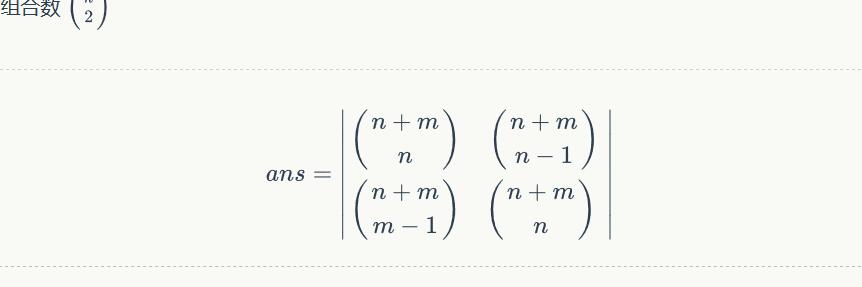
在这里插入图片描述

来源
然后就直接求阶乘，求逆元，然后按照这个行列式乘一下就行了

#include <iostream>
using namespace std;
const int N = 2e3 + 10 ;
const int mod = 1e9 + 7 ; 
typedef long long ll ;
ll f[N] , ff[N];
ll qmi(ll a, ll b)
{
	ll res = 1 ;
	while(b)
	 {
	 	if(b & 1) res = res * a % mod ;
	 	a = a * a % mod ;
	 	b >>= 1 ;
	 }
	 return res ;
}
void init()
{
	f[0] = 1 , ff[0] = 1 ;
	for(int i = 1 ;i < N ;i ++)
	 f[i] = f[i - 1] * i % mod , ff[i] = qmi(f[i] , mod - 2) ;
}
int main()
{
	init() ;
	ll n , m ;
	while(scanf("%lld%lld" , &n , &m) != EOF)
	 {
	 	ll ans = (f[n + m] * ff[n] % mod * ff[m]) % mod ;
	 	ans = ans * ans % mod ;
	 	ans = ans - f[n + m] * ff[n - 1] % mod * f[n + m] % mod * ff[n + 1] * ff[m + 1] % mod * ff[m - 1] % mod ;
	 	ans = (ans + mod) % mod ;
	 	printf("%lld\n" , ans) ;
	 }
	return 0 ;
}

A Path Plan

直接照着模板写

#include <iostream>
using namespace std;
typedef long long ll ;
const int N = 2e5 + 10 ;
const int mod = 1e9 + 7 ;
ll f[N] , ff[N] ;
ll qmi(ll a , ll b)
{
	ll res = 1 ;
	while(b)
	{
		if(b & 1) res = res * a % mod ;
		a = a * a % mod ;
		b >>= 1 ;
	}
	return res ;
}
void init()
{
	f[0] = ff[0] = 1 ;
	for(int i = 1 ;i < N ;i ++)
	 f[i] = f[i - 1] * i % mod , ff[i] = qmi(f[i] , mod - 2) ;
	return ; 
}
int main()
{
	int t ;
	cin >> t ;
	init() ;
	while(t --)
	 {
	 	int x1 , x2 , y1 , y2 ;
	 	cin >> x1 >> x2 >> y1 >> y2 ;
	 	ll ans = f[x1 + y1] % mod * ff[x1] % mod * ff[y1] % mod ;
	 	ans = ans * f[x2 + y2] % mod * ff[x2] % mod * ff[y2] % mod ;
	 	ans -= f[x2 + y1] % mod * ff[x2] % mod * ff[y1] % mod * f[x1 + y2] % mod * ff[x1] % mod * ff[y2] % mod ;
	 	printf("%lld\n" , (ans + mod) % mod) ;
	 }
	return 0 ;
}