逻辑回归以及源码分享

逻辑回归

Logistic回归虽然是一个回归算法，但是不是解决回归问题的算法，而是解决分类问题的算法

logistic函数如下

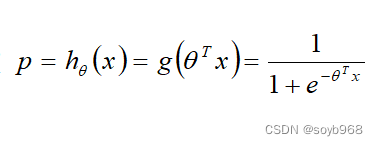
对上述公式进行求导：公式比较简单，可以照着推一边就行

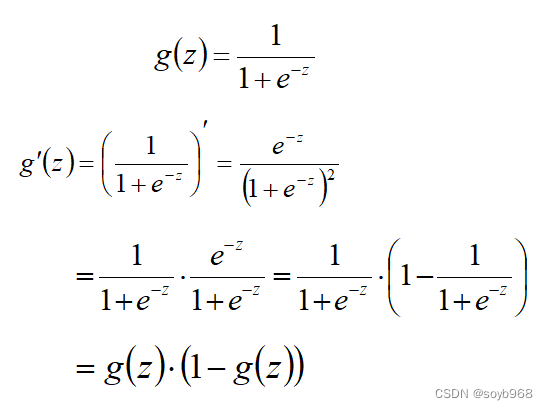
如下图示：Logistic算法是一个分类问题，所以y的取值主要就是1和0，这样的话，其实Logistic回归样本数据符合二项分布，所以能够得到概率方程

其推到如下

注：字写不好，接下来的推导，用wps数学工具写了：

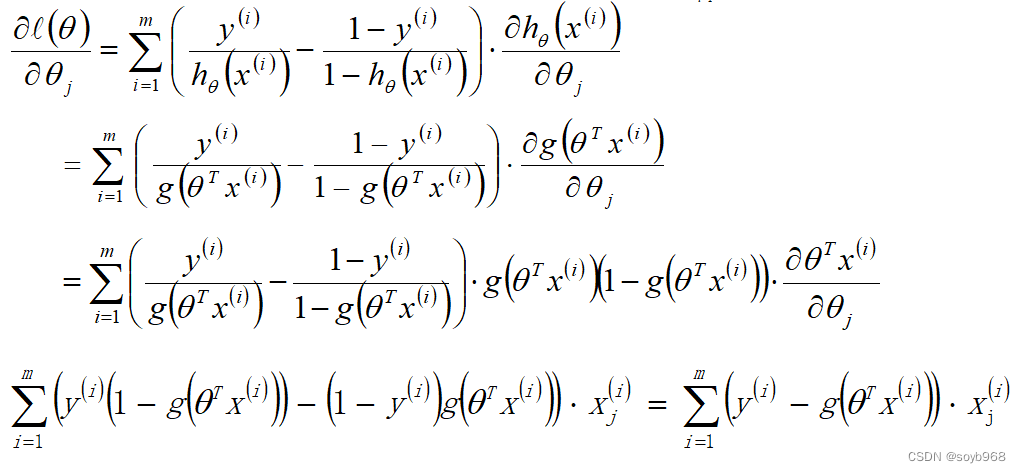
由于在极大似然估计中，当似然函数最大的时候模型最优；而在机器学习领域中，目标函数最小的时候，模型最优；故可以使用似然函数乘以-1的结果作为目标函数

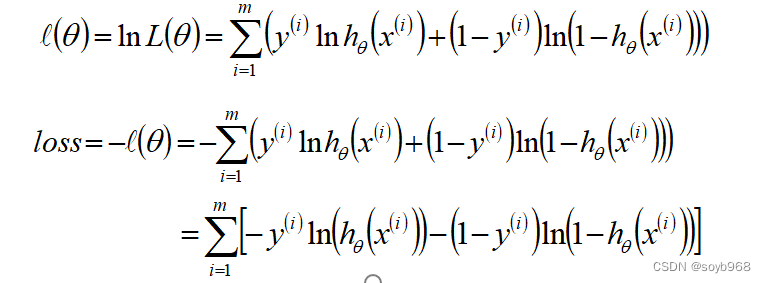
Logistic回归θ参数的求解过程为(类似梯度下降方法): 回顾前面讲的内容

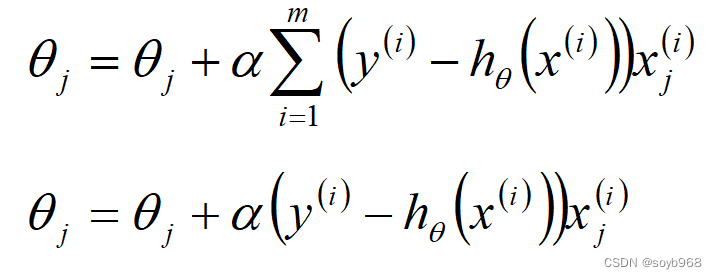
Softmax回归

softmax回归是logistic回归的一般化，适用于K分类的问题，针对于每个类别都有一个参数向量θ，第k类的参数为向量θk，组成的二维矩阵为θk*n；
softmax函数的本质就是将一个K维的任意实数向量压缩（映射）成另一个K维的实数向量，其中向量中的每个元素取值都介于（0，1）之间。
softmax回归概率函数为：

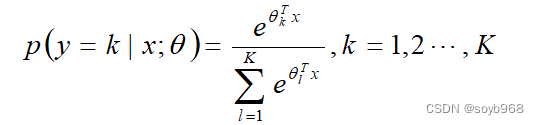
Softmax算法原理：

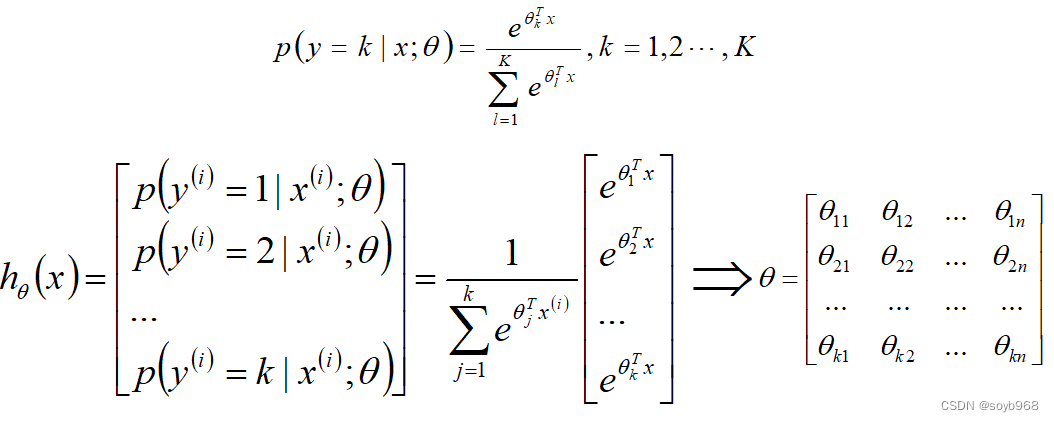
Softmax算法损失函数

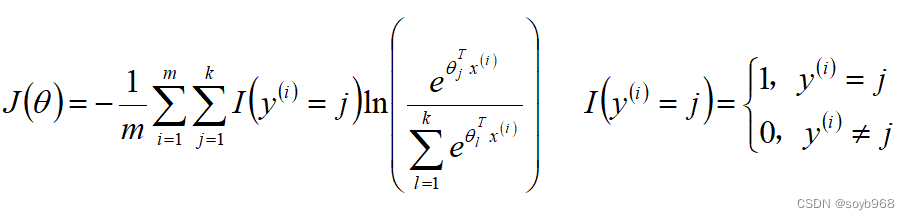
Softmax算法梯度下降法求解

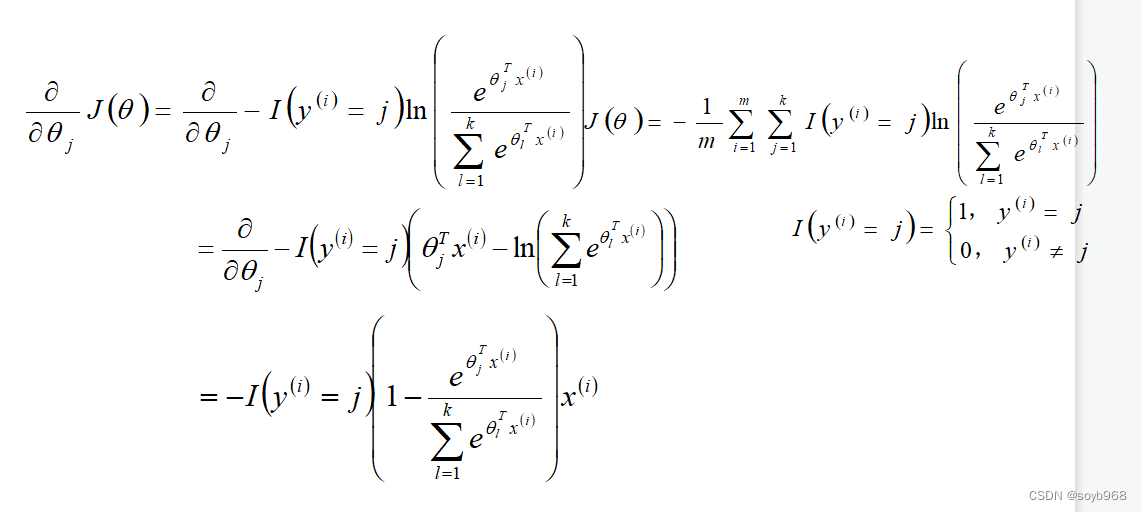
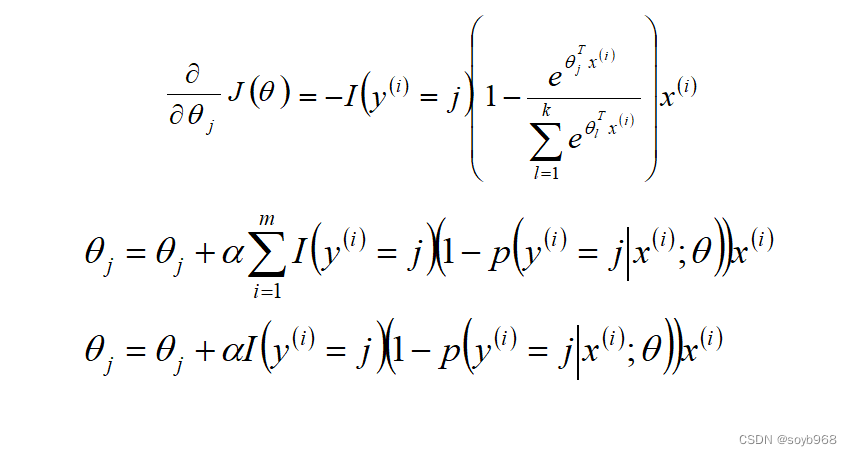
Logistic案例：乳腺癌分类

数据来源：data

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import pandas as pd
import warnings
import sklearn
from sklearn.linear_model import LogisticRegressionCV,LinearRegression
from sklearn.linear_model.coordinate_descent import ConvergenceWarning
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
## 设置字符集，防止中文乱码
mpl