【数学建模】关联与因果问题

一、灰色关联

1、基本概念

灰色系统：部分信息已知而部分信息未知的系统，我们称之为灰色系统。相应的，知道全部信息的叫白色系统，完全未知的叫黑色系统。

适用领域：小样本（数据不足）、样本没有较好的统计分布规律

基本步骤：

1. 消除量纲
   对初始数据进行一系列处理，方法包括初值化变换，均值化变换，百分比变换，倍数变换等。一般我们选用一种进行量纲消除。
2. 计算关联系数
   
3. 计算关联度
   
   进而我们可以分析结果

2、关联分析

首先来看一则经典案例

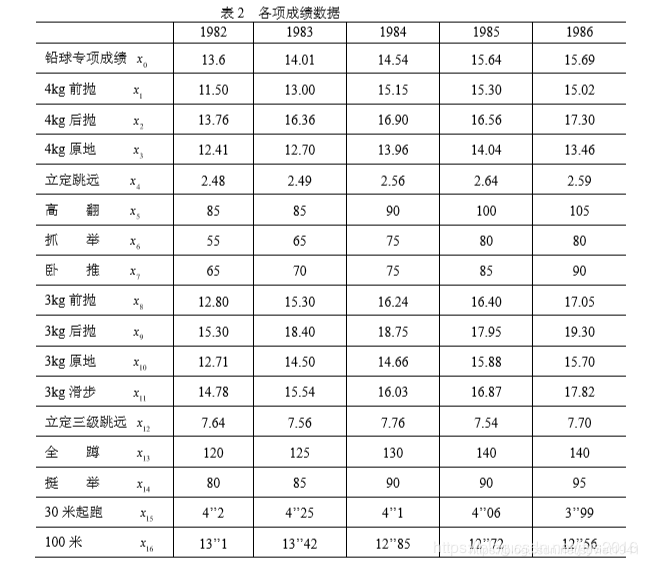
关联分析主要解决 因素之间关联性如何，关联程度如何量化的问题

例如，4kg前抛到100米成绩这16个因素与铅球专项成绩的关系，就属于灰色关联需要解决的问题。

对目标铅球专项成绩数列，我们称为参考数列。

对16个影响因素数列，称为比较数列。

其中我们需要注意，前14项数据属于数值越大越优秀，后2项属于数值越小越优秀，在处理数据需要做不同的处理。

%示例
load x.txt   %把原始数据存放在纯文本文件 x.txt 中
for i=1:15     
    x(i,:)=x(i,:)/x(i,1);   %标准化数据，越大越好 
end
for i=16:17     
    x(i,:)=x(i,1)./x(i,:);  %标准化数据，越小越好
end
data=x; 
n=size(data,2); %求矩阵的列数，即观测时刻的个数 
ck=data(1,:);  %提出参考数列 
bj=data(2:end,:); %提出比较数列 
m2=size(bj,1); %求比较数列的个数 
for j=1:m2       
    t(j,:)=bj(j,:)-ck; 
end
mn=min(min(abs(t')));  %求小差
mx=max(max(abs(t')));  %求大差
rho=0.5;  %分辨系数设置 
ksi=(mn+rho*mx)./(abs(t)+rho*mx);  %求关联系数 
r=sum(ksi')/n  %求关联度 

r代指各个指标的关联度

%在上式中，r结果为
r =    0.5881    0.6627    0.8536    0.7763    0.8549    0.5022    0.6592    0.5820    0.6831    0.6958    0.8955    0.7047    0.9334    0.8467    0.7454    0.7261

因此，全蹲，三公斤滑步等项目对铅球专项成绩的影响较大。

3、优势分析

当数据中有了多个参考数列，即多个影响结果。

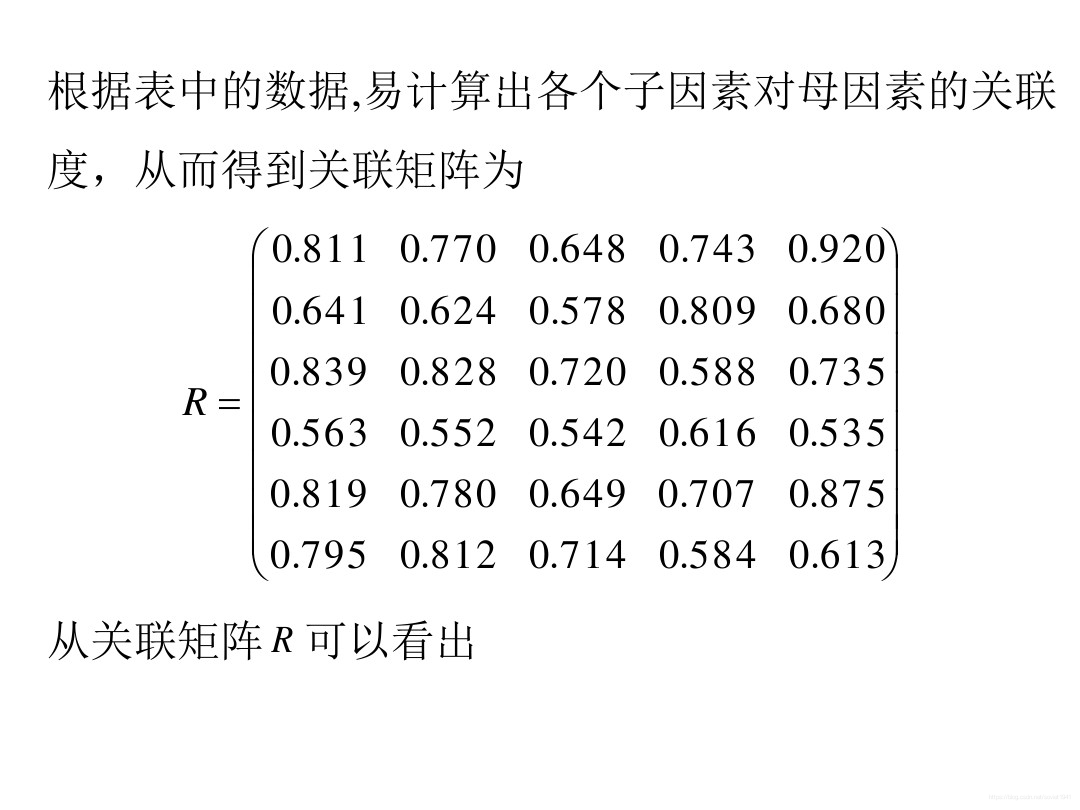
我们需要求出其关联矩阵。其中rij代表第j个子因素对第i个母因素的影响。

当某行元素大于其他行元素，称之为优势母元素；某列元素大于其他列元素，称之为优势子元素。

我们来看下列案例：

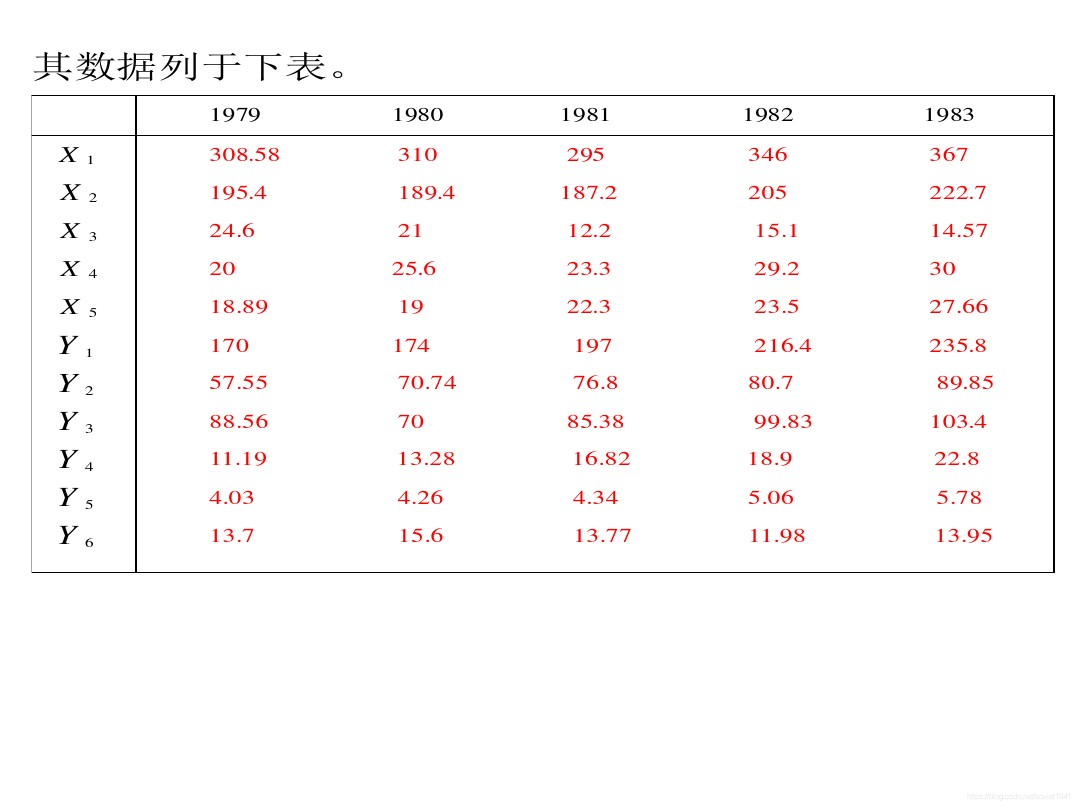
%示例
data=load data.txt
n=size(data,1);
for i=1:n
	data(i,:)=data(i,:)/data(i,1);	%标准化数据，属于越大越好
end
ck=data(6:n,:);m1=size(ck,1);	%提出参考数列
bj=data(1:5,:);m2=size(bj,1);	%提出比较数列
for i=1:m1
  for j=1:m2
    t(j,:)=bj(j,:)-ck(i,:);
  end
  jc1=min(min(abs(t')));
  jc2=max(max(abs(t')));
  rh0=0.5;
  ksi=(jc1+rho*jc2)./(abs(t)+rho*jc2);	%求关联系数
  rt=sum(ksi')/size(ksi,2);
  r(i,:)=rt;	%求关联度
 end
 r

结果评价：

参考资料：
数模day13-灰色系统理论I-灰色关联与GM(1,1)预测
数学建模常用模型04 ：灰色关联分析法
数学建模之灰色关联实例含代码
数学建模——灰色关联度的分析

二、典型相关分析

1、基本概念

传统的相关分析，只要求X的每一个变量与Y的每一个变量的相关系数，从而组成相关系数矩阵 R = [rij]p*q ,rij表示第i个自变量xi与第j个因变量yj之间的相关系数。

然而，这是有缺陷的：只粗暴的考虑了X与Y的关系，却忽略了X自变量之间也可能有相关关系，Y因变量之间亦如此。我们不仅需要考虑两个变量之间的相关程度，而且还需要考察多个变量与多个变量之间的相关性。

解决的方法类似于主成分分析，我们可以把X提取出主成分，Y也提取出主成分，从而X、Y内部线性不相关了，这样利用主成分研究X与Y之间相关性就解决了上述缺点。

典型相关分析一般用于变量数目较多的情况。

2、使用办法

步骤：

1. 计算相关系数矩阵
2. 计算典型相关系数和典型变量
3. 典型相关系数的显著性检验
4. 随后，对原始两组数据的研究可以转化为对典型变量的研究

下面，我们来看一个例子：

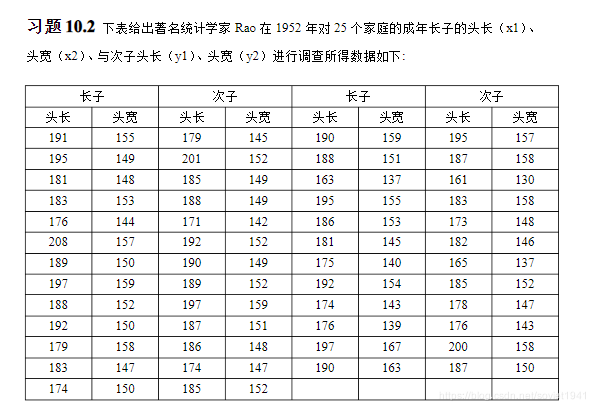
x=load data.txt
%第一步，计算相关系数矩阵程序
R=corrcoef(x)
%第二步，计算典型相关系数和典型变量
R11=R([1,2],[1,2]);
R12=R([1,2],[3,4]);
R21=R([3,4],[1,2]);
R22=R([3,4],[3,4]);
A=(R11^(-1))*R12*(R22^(-1))*R21;
B=(R22^(-1))*R21*(R11^(-1))*R12;
[X1B1]=eig(A);
[X2B2]=eig(B);
s=cov(x);
s1=s([1,2],[1,2]);
s2=s([3,4],[3,4]);
s1(1,2)=0;
s1(2,1)=0;
s2(1,2)=0;
s2(2,1)=0;
B1=B1^(1/2)
l=(s1^(-1))*X1
B2=B2^(1/2)
m=(s2^(-1))*X2

随后进行显著性检验，可以看出对原始两组变量的研究可转化为对第一对典型变量的研究，通过它们之间相关性的研究来反映原始两组变量的相关关系。

其实感觉典型相关分析用SPSS的多一点，这个以后再说吧

参考资料：
数学建模——典型相关分析（CCA）及spss操作过程
典型相关分析（Matlab实现函数）
数学建模__SPSS_典型相关分析