本文深入探讨数据结构核心，包括线性表、数组、链表、桶排序、基数排序、树、二叉查找树、平衡二叉树、B树、散列、堆、排序算法等，解析各数据结构的特点及应用场景。
线性表
- 数据结构的物理形式
数组: 选择和搜索较快O(1), 插入和删除较慢O(n)
链表: 插入和删除较快O(1), 选择和搜索较慢O(n) - 桶排序： O(n+m) 其中m为桶的个数。每个桶是一个链表实现的线性表，链表尾部插入
- 基数排序：O((n+b)logb m) 其中b是基数,m为桶的个数。
- 基数排序在每一位上而不是整个数做桶式排序，位排序的顺序是低位优先,基于前面一趟的桶排序进行桶排序，最后顺序扫描各个桶得到有序输出
- 基数排序和桶式排序不同的地方：同一个桶中的数可以不同
- 堆栈的应用：符号平衡、后缀表达式求值、递归调用的实现
- 队列：FIFO队尾rear进或插入，队头front出或删除。为了防止队头队尾同时挤压到最后，最好使用循环链表。
树
-
节点的深度：根到节点的唯一路径的长（一般从1开始）
节点的高度：节点到它的树叶最长路径的长（一般从1开始）
树的高度和树的深度（类似于节点）
内部节点：非叶子节点 -
先序遍历应用：层次缩进打印目录内容
后序遍历应用：计算目录内容大小- 先序：根左右 中序：左根右 后序：左右根
- 后缀表达式->表达式树的方法：借助栈，扫描后缀表达式，若遇到数字，构造单节点树，入栈；若遇到操作符，从栈中弹出两棵树，以操作符为根，合并弹出的两棵树，将得到的树入栈。
-
二叉查找树BST
-
BST的Find操作 ---- 递归法，迭代法
-
BST的Insert操作---- 递归法，迭代法（迭代比较，直到对应分支为NULL，插入）
-
BST的删除操作
----没有左右子节点，可以直接删除
----存在左节点或者右节点，删除后将子节点挂到对应父节点上
----同时存在左右子节点，通过和后继节点交换后转换为前两种情况后继节点：当某个节点存在右节点时，后继结点就是右节点中的最小值，因此后继节点一定没有左节点。所以，后继结点有可能存在右节点，也有可能没有任何节点。由于后继结点最多只有一个子节点，因此通过交换后继节点再删除后，就变成了 3 种情况中的前两种
推荐：二叉查找树 - 删除节点 详解(Java实现)
代码实现：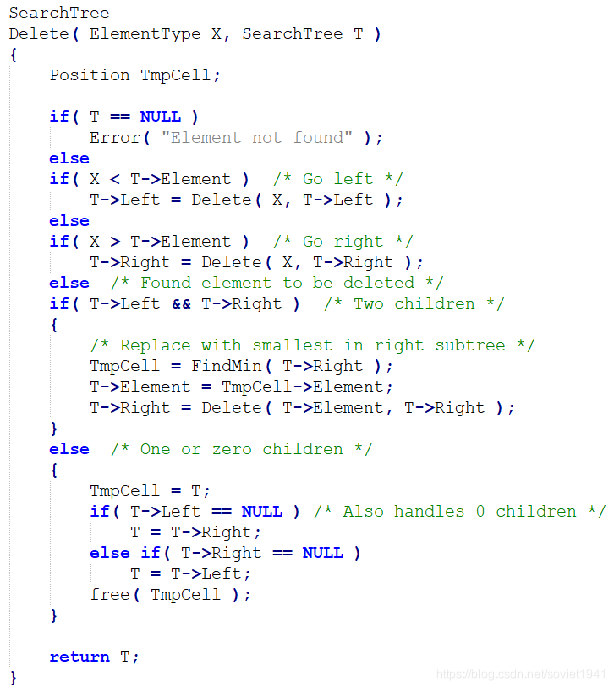
在平衡性良好的情况下，查找插入删除O(log n)，最坏代价达到O(n)
-
-
平衡二叉树AVL
平衡二叉树AVL是一种任意节点的左右子树深度或高度相差最多为1的BST，AVL树的高度最大为O(logN)-
4种不平衡情况
左儿子的左子树插入（左左）
右儿子的右子树插入（右右）
左儿子的右子树插入（左右）
右儿子的左子树插入（右左）
策略：1和2单旋转调整；3和4双旋转调整 -
示例：
在左左情境下，K2是搜寻出问题的节点。对于K2来说，先让他左膀的右臂成为他的左膀，再成为他左膀的右臂（2步操作）。双旋转示例(右左)：
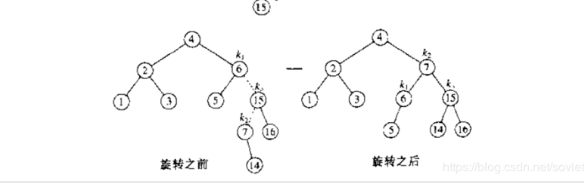
代码（右左）：
对于左右，先对右节点 右右处理，转化成左左；再进行左左处理
对于右左，先对左节点 左左处理，转化成右右；再进行右右处理
-
-
B树
- M阶B树满足树根有2到M儿子；非根内部节点最少有ceil(M /2)个儿子，最多有M个儿子。这里ceil代表向上取整 。有k个儿子的内部节点，有k-1个关键字，升序排列。B树的高度: O(logM N)。 插入和删除可以接近常数时间，从而减少磁盘I/O次数。
- 查找代价：O(logM N)
- 插入代价（一般）：O(M) 最坏代价：O(MlogM N)
操作：由根向树叶查找，确定插入的树叶位置，插入。若树叶满，M+1关键字的节点分裂成floor((M+1)/2)和ceil((M+1)/2)个关键字的两个节点，父节点儿子树相应增加，可能一直分裂到根，从而增加B树的深度。//（我也不是很懂） - 删除最坏代价 ：O(MlogM N)
散列
- 基本概念
哈希函数： 将元素转换成可以查找的整数关键字，将理论上无限的元素映射到有限的哈希表地址空间
哈希表：一种可以平均常数时间查找、插入和删除的数据结构
冲突：多个元素会映射到表中同一个位置 - 哈希性质
均匀哈希：每个关键字的探查序列等可能的是0-m-1中排列的任一种。
简单均匀哈希：任何一个给定元素等可能的哈希到m个单元中任意一个，且与其他元素哈希到什么位置无关。
哈希表大小的选择：最接近目标需求的素数
平均情况下，哈希表的查找、插入和删除性能是常数时间 - 冲突处理
-
分离链接法：将哈希到同一个单元的元素用链表连接起来
装填因子λ=元素个数n/哈希表的大小=链表的平均长度
平均情况分析（λ=O(1)）：
不成功的查找: λ 次比较(1+λ)
成功查找平均情况：1+λ/2（1+λ）
插入：1+λ
删除：1+λ/2（1+λ）最坏情况分析(λ=O(N),所有元素哈希到同一链表，O(N))
不成功的查找O(N)
成功查找O(N)
插入O(N)
删除 O(N) -
开放寻址法
- 线性探测
- hi(k) = h(k) + i，只要表未满，线性探测保证元素可插入。
哈希单元三种状态：空、删除和有效占用位置。删除标记的单元可以插入元素，可以继续往下查找。 - 插入和不成功查找的期望探测次数为：(1+1/(1-λ)²)/2。
成功查找的期望探测次数为：(1+1/(1-λ))/2，比不成功次数少。 - 随机探测，不成功查找的期望探测次数（找到一个空单元）为：1/(1-λ)。
- hi(k) = h(k) + i，只要表未满，线性探测保证元素可插入。
- 二次探测（平方探测）
hi(k) = h(k) + i², h(k) = k % 10。即使表未满，二次探测下的插入也可能失败。- 二次探测定理：表至少有一半是空的时候，总能插入一个新的元素
- 线性探测
-
- 再散列
当负载因子达到一定程度（或插入失败时），例如0.5，创建一个2倍大小的新哈希表，使用一个新的相关哈希函数将旧哈希表中的元素放到新哈希表中。代价为O(n)。
堆
1. 优先队列
优先队列的出队基于元素的优先级，优先级最小或最大的元素先出队。按照类别可分为：最小优先队列（优先级最小的先出队，默认），最大优先队列（优先级最大的先出队）：堆排序。
2. 二叉堆
二叉堆是实现优先队列的一种重要方法。
分类：最小堆（最小优先队列）和最大堆（最大优先队列）
基本性质：
结构性：完全二叉树；
堆序性：任意节点小于（或大于）它的后裔；每颗子树都是一个堆。
1. 堆的初始化
其中，堆结构体里定义了堆的数组，大小和容量。在建堆时，堆的数组大小要比最大容量大一，因为要在数组的0位置设置一个哨兵元素，方便插入操作。
2. 插入（入队）
将新插入的元素放到堆尾。若新插入的元素比父亲大，父亲下沉，新插入元素上滤，直到比父亲大为止 。最坏情况下的代价：O(logN)
3. 删除（出队）
删除树根，两棵子树是二叉堆，但结构性破坏。将二叉堆最后的元素放入树根，结构性质、满足，堆序破坏。将新的树根和两个儿子比较，若有儿子大，大的儿子上升，新根下滤，直到比所有儿子小为止。 最坏情况下的代价：O(logN)
4. 构建堆
自顶而下的建堆方式：从根结点开始，把结点一个个插入堆中。当把一个新的结点插入堆中时，需要对结点进行调整，以保证堆依然是大根堆。时间复杂度为O(logN)。
自下而上的建堆方式：从最后一个内部节点直到根进行堆序性质维护。操作N次，时间复杂度为O(N)。
3. 堆排序
思想：将N个元素构建一个最大堆
重复N-1次以下过程：
1 将堆顶元素（最大元素）和堆中最后的元素交换
2 堆的大小减1
3 维护堆使得满足最大堆性质
其中，PercDown指的是下滤，即维护堆。上面的初始化堆代价为O(N)，下面的删除后维护代价为O(logN)，总的时间复杂度为O(NlogN)。
排序
稳定性：任意两个相等的数据，在排序前后相对位置不改变。
冒泡排序
- 最好代价O(N)，最坏代价O(N²)，平均代价O(N²)。
- 具有稳定性。
插入排序
- 维护一个有序区。
- 最好代价O(N)，最坏代价O(N²)，平均代价O(N²)。
- 具有稳定性。
基于相邻元素两两交换的排序每次只能消除一对逆序对，平均代价和最坏代价均为O(N)。
希尔排序
- 减小增量序列，对每个增量序列进行插入排序。
- 平均时间代价小于O(N²)，约等于O(logN)。最坏代价达到O(N²)。
- 使用Hibbard增量的希尔排序每次增量为2^k-1，保证增量序列之间互质，最坏时间代价约为O（N ^ 2/3）。
- 希尔排序是不稳定的。
堆排序
见上一节
归并排序
- 合并子程：设置三个指针，进行判断和移动。需要额外空间。时间复杂度O(N)。
- 递归的算法：先划分成两个子问题，再进行合并。需要额外空间，总时间复杂度O(NlogN)。
- 归并排序是稳定的。
快速排序
- 时间复杂度O(logN)，最坏情况为O(N^2)
- 操作流程：首先选取一个pivot，作为分割的参考值。比它小的放到左边，比它大的放到右边。选取pivot的方法常用三数取中值，最后将中值放到right -1的位置。
在某一次特定的递归时，用两个指针进行比较，左边大于右边小于时交换。当右指针小于左指针时停止，并将pivot和左指针交换。 - 快排缺点：需要大量堆栈空间。因此，在数据量小时，常采用插入排序。
- 快速排序是不稳定的。
图
图的表示
- 图的邻接矩阵表示：简单直观，方便统计出度和入度。但在稀疏图情况下浪费时间和空间。
- 邻接链表表示：在稀疏图情况下节省时间空间，但在稠密图情况下浪费时间空间。此外，邻接链表不方便统计节点的入度，需要额外构建逆邻接链表。
图的遍历
- DFS深度优先搜索
类似于树的先序遍历。沿着一条路走下去，然后逐层检测逐层退出。空间存储类似于堆栈。
void DFS(Vertex V){
visited[V] = true;
for(V的每个邻接点W){
if(!visited[W]){
DFS(W);
}
}
}
时间复杂度：邻接表 O(N+E)
邻接矩阵O(N^2)。
- BFS广度优先搜索
类似于树的层序遍历。遍历每一层的节点压入优先队列，弹出时再压入其邻接节点。如此循环完成每一层的遍历。
void BFS(Vertex V){
visited[V] = true;
Enqueue(V,Q);
while(!isEmpty(Q)){
V = Dequeue(Q);
for(V的每个邻接点W){
if(!visited[W]){
visited[W] = true;
Enqueue(W,Q);
}
}
}
}
时间复杂度：邻接表 O(N+E)
邻接矩阵O(N^2)。
拓扑排序
- 拓扑序：如果从V到W有一条有向序列，那么在排序里V一定在W之前。合理的拓扑序必定是一个有向无环图。
- 操作过程：每次找出入度为0的节点，将其输出，并把所有与之相邻的节点入度减一（相当于删去这个点）。如果循环还未结束已经找不到p入度为0的节点，则说明这个图里有环。
void TopSort(){
int cnt = 0;
for(图中每个顶点V){
if(Indegree[V] == 0)
Enqueue(V,Q);
}
while(!isEmpty(Q)){
V = Dequeue(Q);
输出V
cnt++;
for(V的每个邻接点W){
if(--Indegree[W] == 0)
Enqueue(W,Q);
}
}
if(cnt != |V|)
Error("图中有回路");
}
时间复杂度： O(N+E)
扫一扫
6465
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
