AcWing 1214. 波动数列 解题思路及代码

先贴个题目：

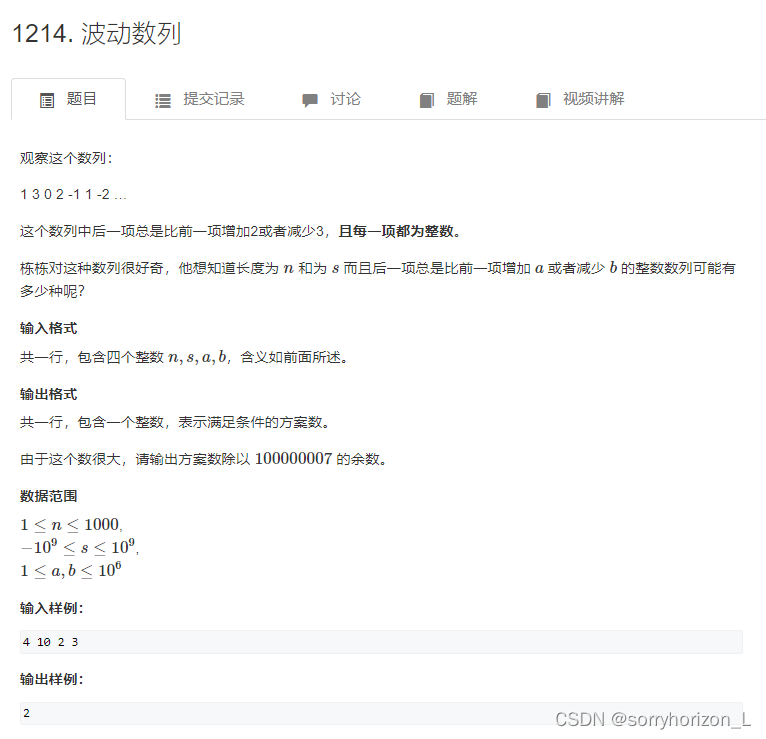
 以及原题链接：1214. 波动数列 - AcWing题库https://www.acwing.com/problem/content/1216/

 这题其实我个人觉得比地宫取宝简单，因为地宫取宝要开个四维数组，可能是我题做的少了，确实是不是很敢去思考四维数组的可能行，而这题和k倍区间有相同思路，我们可以先做个计算，设第一个数是x，那么设数列是+a，-b都是d，那么可以得出，第二个数就是x+d(n-1),第三个数就是x+d（n-1）+d（n-1）所以全部数列相加就是

变形后可得因为第一个数不好确认，我们就可以把他表示出来，然后可以发现，S减去后面的一大串数是n的倍数，因为x必为整数。那么就可以利用

(a-b)%n=0等价于a%n=b%n的定理，把dp设为两个维度，一个是到第几个d，一个是余数。

来看看代码：

#include<iostream>
using namespace std;

const int N = 1010;
const int MOD = 100000007;

int dp[N][N];

int mod(int num,int x)
{
    int y = (num % x + x) % x;
    return y;
}

int main()
{
    int n, s, a, b;
    cin >> n >> s >> a >> b;
    dp[0][0] = 1;
    for (int i = 1; i < n + 1;++i)
        for (int j = 0; j < n;++j)
        {
            dp[i][j] = (dp[i - 1][mod(j + i * a, n)] + dp[i - 1][mod(j - i * b, n)]) % MOD;
        }
    cout << dp[n - 1][mod(s, n)];
    return 0;
}

需要说明的是，这里需要一个技巧，在数论中的负数取余和计算机的取余是不一样的，举个例子，-2%10数论上是等于8，而计算机会输出-2，所以需要一个取模函数来解决这个问题

int mod(int num,int x)
{
    int y = (num % x + x) % x;
    return y;
}

这个函数就是这个功能，然后就没什么好说了。

by————2024.2.14刷题记录