2.1、机器学习-模型评估指标与参数调优

原创已于 2025-09-21 12:53:40 修改 · 958 阅读

12 ·

CC 4.0 BY-SA版权

文章标签：

#机器学习 #算法 #人工智能

于 2025-09-21 12:53:16 首次发布

人工智能同时被 2 个专栏收录

21 篇文章

订阅专栏

机器学习

5 篇文章

订阅专栏

模型评估指标（如准确率、精确率、召回率、F1分数、AUC-ROC及对数损失等）为量化模型性能提供客观依据，进而通过参数调优（如网格搜索、随机搜索或贝叶斯优化等技术）系统性地调整超参数，以优化模型在验证集上的表现，最终目标是提升泛化能力并在未知数据上实现最佳性能。

1、分类问题常用评估指标

分类问题是机器学习领域最常见的大类问题，很多场景都可以规划到分类问题的解决范畴。对于分类问题来说，常用的评估指标主要包括以下几种：

混淆矩阵
准确率(Accuracy)
精确率(Precision)
召回率(Recall)
F1-Score
ROC曲线
AUC值
KS曲线

1.1、混淆矩阵

混淆矩阵(Confusion Matrix)是一种有效的评估模式，特别适用于监督学习。典型的混淆矩阵构成如图所示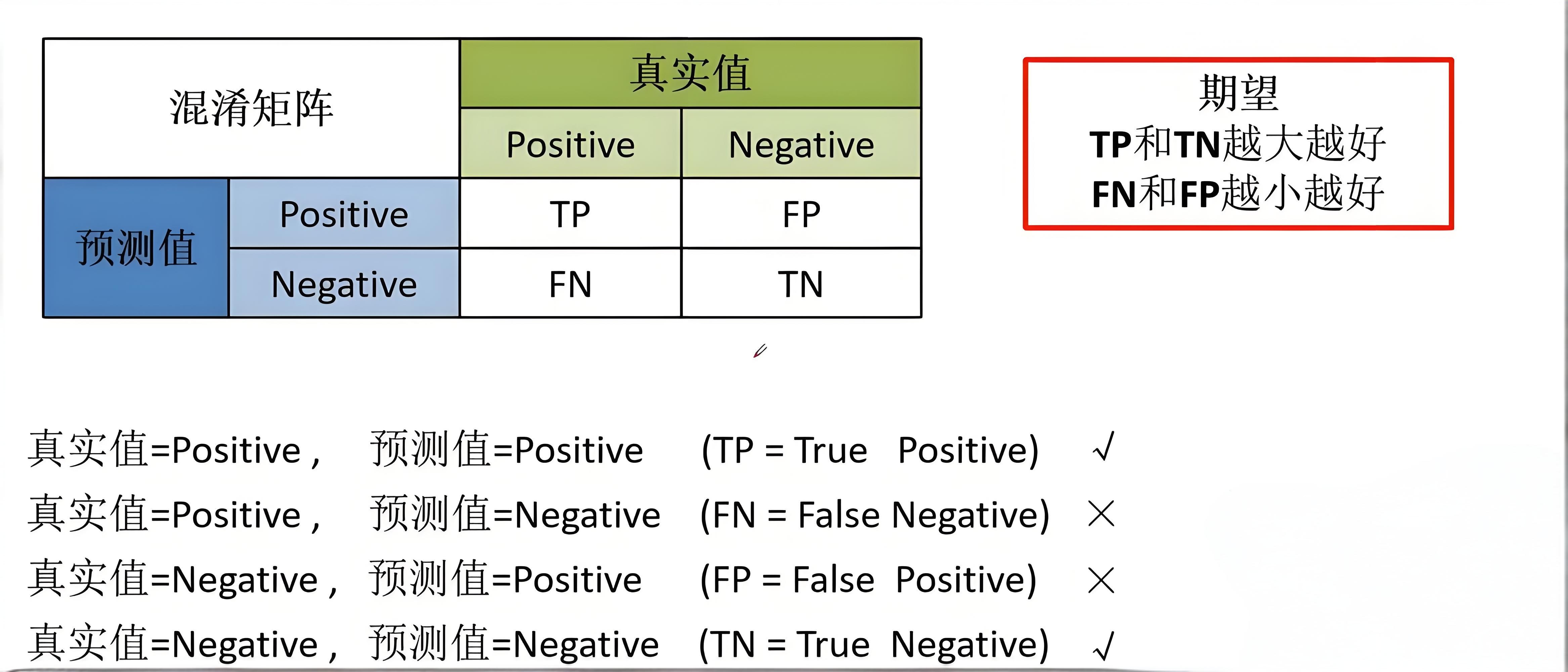：包括准确率、精确率、召回率在内的很多指标，都可以基于混淆矩阵计算得到。

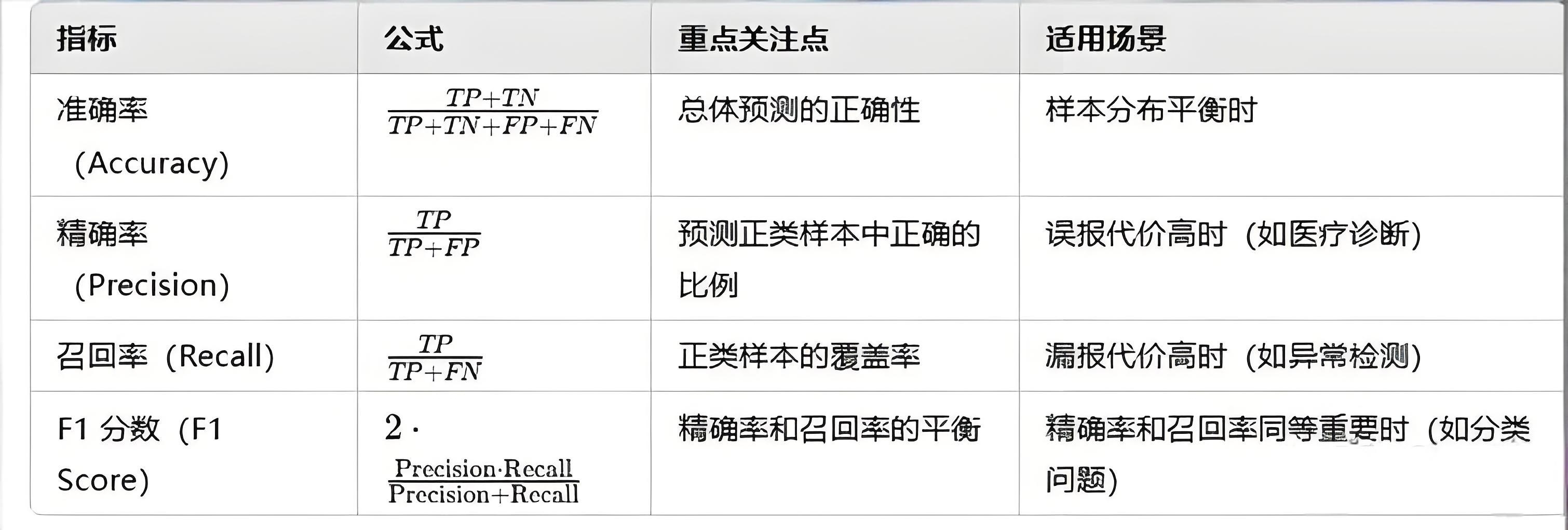
准确率(Accuracy)：分类正确样本占样本总数的比例。

$Accuracy=\frac{TP +TN}{TP+TN+FP+FN}$

精确率(Precision)：识别为正类的样本中，真正为正类的样本所占的比例。

$Precision=\frac{TP}{TP+FP}$

召回率(Recall)：识别正确的样本，占总体正类样本的比例

$Recall= \frac{TP}{TP+FN}$

F1-Score：综合考虑精确率和召回率的评估指标，F1值较高说明模型性能较好。

$F1 =2\times \frac{Precision\times Recall}{Recallsion+Recall}$

1.2、ROC曲线

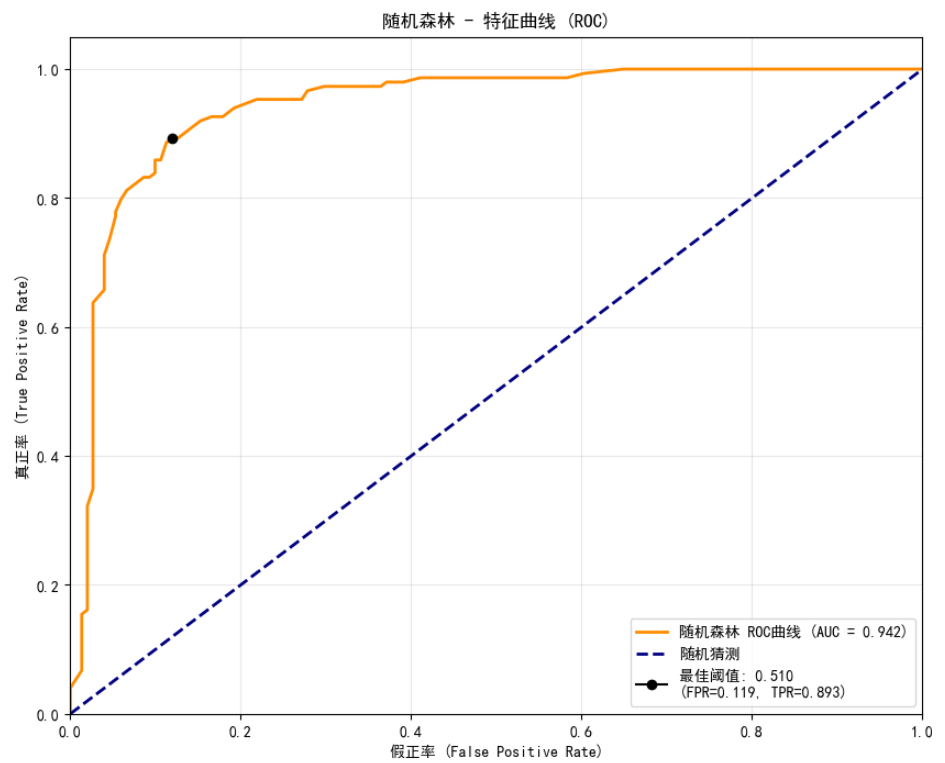
对于二分类模型来说，ROC曲线和KS曲线是主要的评估手段。以ROC曲线为例，它主要体现了学习器在不同任务下，TPR和FPR随阈值的变化情况：

对于ROC曲线来说，曲线越接近左上角，表示该分类器的性能越好。

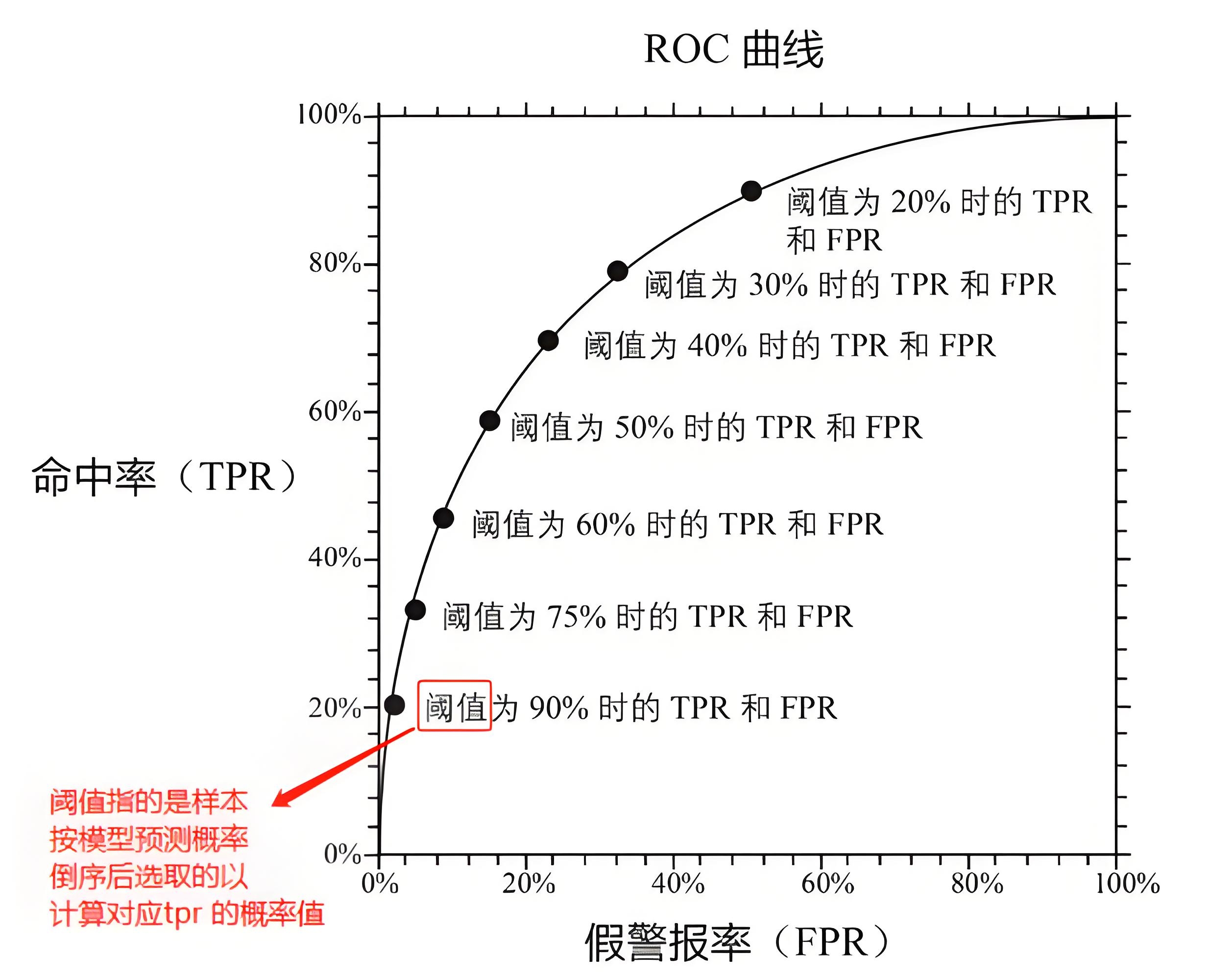
借助AUC值(定义为ROC曲线下与坐标轴围成的面积)，可以量化ROC曲线反映的模型性能，它对应ROC曲线所覆盖的面积(范围在[0, 1]之间)。ROC曲线一般在y=x曲线上方，所以AUC的取值范围一般在（0.5~1）。

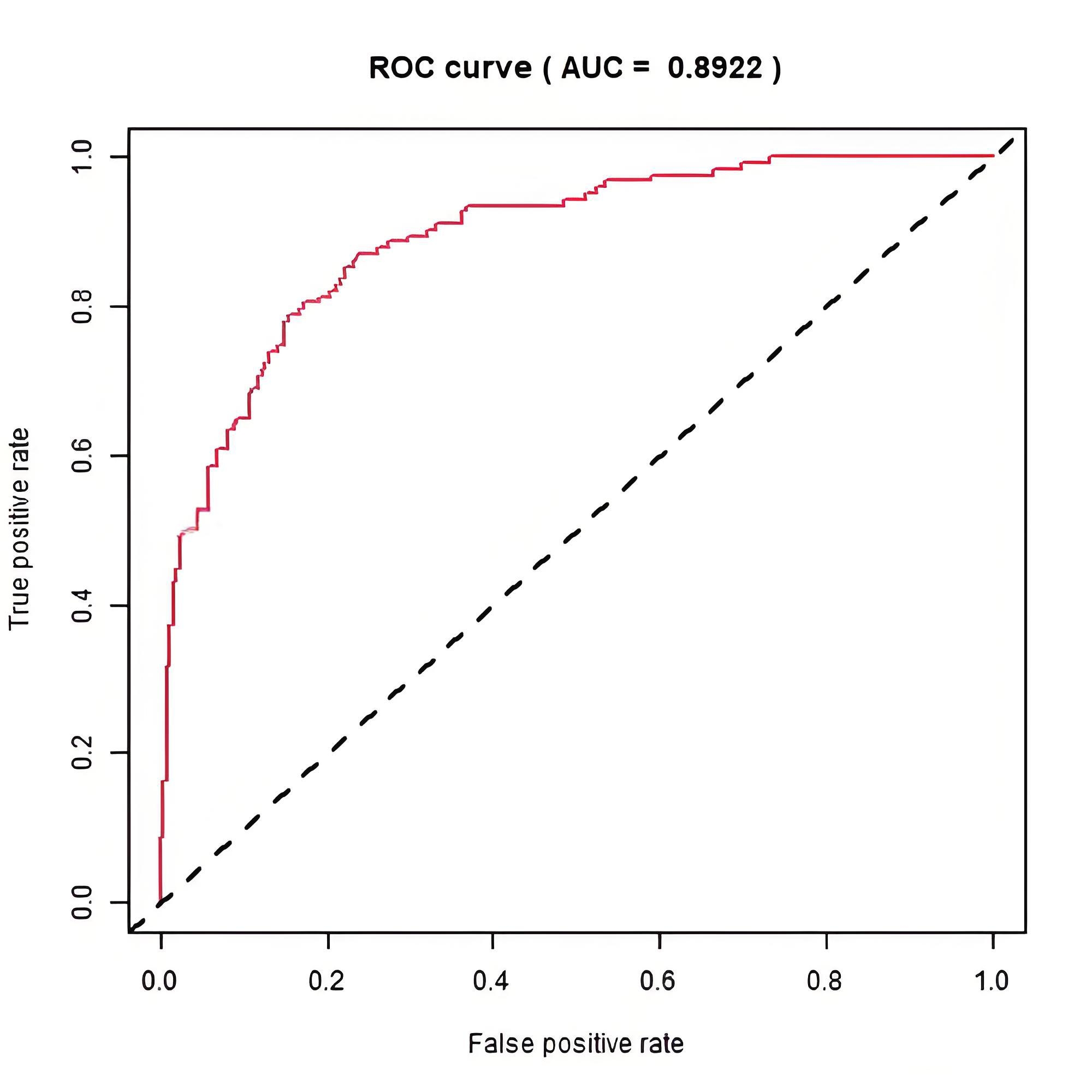
AUC = 1：完美分类器
0.5< AUC <1：优于随机猜测，数值越大性能越好
AUC = 0.5：相当随机测，模型约有预测价值
AUC < 0.5：比随机猜测还要差，或许能用于反向预测

示例：逻辑回归和随机森林分类模型ROC曲线比较。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import (
    roc_curve, 
    auc, 
    roc_auc_score, 
    confusion_matrix, 
    classification_report
)
from scipy.stats import ks_2samp
import seaborn as sns

# 设置中文字体支持
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False    # 用来正常显示负号

# 生成模拟分类数据
X, y = make_classification(
    n_samples=1000, 
    n_features=10, 
    n_informative=8, 
    n_redundant=2,
    random_state=42
)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=42
)

# 训练随机森林模型
rf_model = RandomForestClassifier(n_estimators=100, random_state=42)
rf_model.fit(X_train, y_train)

# 获取预测概率（正类的概率）
y_pred_prob_rf = rf_model.predict_proba(X_test)[:, 1]

# 训练逻辑回归模型作为对比
lr_model = LogisticRegression(random_state=42)
lr_model.fit(X_train, y_train)
y_pred_prob_lr = lr_model.predict_proba(X_test)[:, 1]


def plot_roc_curve(y_true, y_pred_prob, model_name="Model"):
    """
    绘制ROC曲线并计算AUC值
    
    参数:
    y_true: 真实标签
    y_pred_prob: 预测为正类的概率
    model_name: 模型名称
    """
    # 计算ROC曲线点
    fpr, tpr, thresholds = roc_curve(y_true, y_pred_prob)
    
    # 计算AUC值
    roc_auc = auc(fpr, tpr)
    
    # 绘制ROC曲线
    plt.figure(figsize=(10, 8))
    plt.plot(fpr, tpr, color='darkorange', lw=2, 
             label=f'{model_name} ROC曲线 (AUC = {roc_auc:.3f})')
    plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--', label='随机猜测')
    
    # 设置图形属性
    plt.xlim([0.0, 1.0])
    plt.ylim([0.0, 1.05])
    plt.xlabel('假正率 (False Positive Rate)')
    plt.ylabel('真正率 (True Positive Rate)')
    plt.title(f'{model_name} - 特征曲线 (ROC)')
    plt.legend(loc="lower right")
    plt.grid(True, alpha=0.3)
    
    # 找到最佳阈值（最靠近左上角的点）
    gmeans = np.sqrt(tpr * (1 - fpr))
    ix = np.argmax(gmeans)
    best_threshold = thresholds[ix]
    
    plt.plot(fpr[ix], tpr[ix], marker='o', color='black', 
             label=f'最佳阈值: {best_threshold:.3f}\n(FPR={fpr[ix]:.3f}, TPR={tpr[ix]:.3f})')
    
    plt.legend(loc="lower right")
    plt.show()
    
    return fpr, tpr, roc_auc, best_threshold

# 绘制随机森林模型的ROC曲线
fpr_rf, tpr_rf, auc_rf, best_threshold_rf = plot_roc_curve(y_test, y_pred_prob_rf, "随机森林")

# 绘制逻辑回归模型的ROC曲线
fpr_lr, tpr_lr, auc_lr, best_threshold_lr = plot_roc_curve(y_test, y_pred_prob_lr, "逻辑回归")

# 比较两个模型的ROC曲线
plt.figure(figsize=(10, 8))
plt.plot(fpr_rf, tpr_rf, color='darkorange', lw=2, 
         label=f'随机森林 ROC曲线 (AUC = {auc_rf:.3f})')
plt.plot(fpr_lr, tpr_lr, color='green', lw=2, 
         label=f'逻辑回归 ROC曲线 (AUC = {auc_lr:.3f})')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--', label='随机猜测')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('假正率 (False Positive Rate)')
plt.ylabel('真正率 (True Positive Rate)')
plt.title('模型比较 - 特征曲线 (ROC)')
plt.legend(loc="lower right")
plt.grid(True, alpha=0.3)
plt.show()

1.3、KS曲线

KS曲线和ROC曲线在本质上相同，也是关注TPR 和FPR。

KS曲线同样希望TPR尽可能高，FPR尽可能低，区别主要在于横纵坐标的设置。

KS曲线将阈值作为横坐标，将命中率(TPR)与假报警率(FPR)的差值作为纵坐标。KS曲线通过KS值来衡量模型的预测效果：

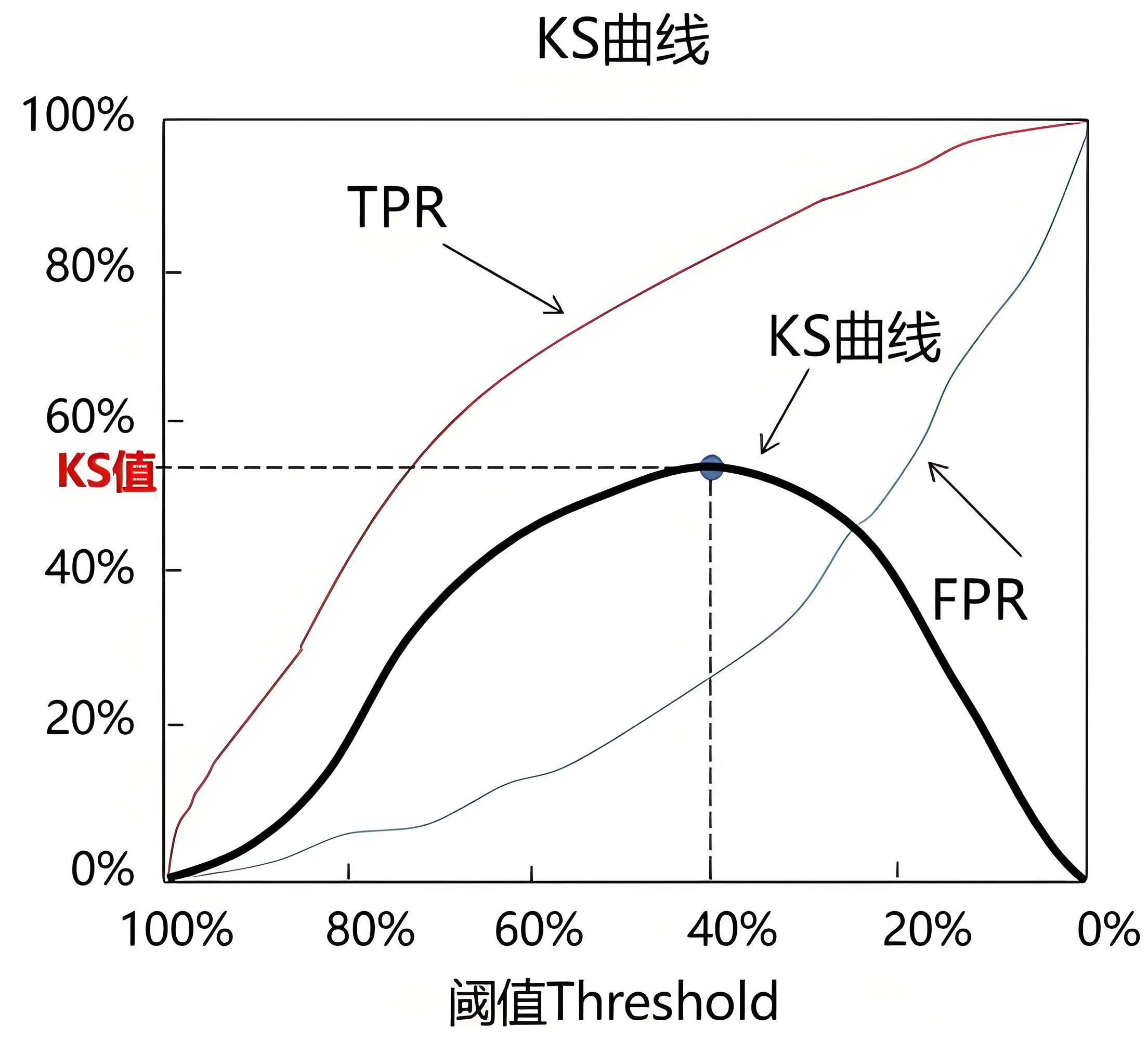
KS值的计算方式：KS=max(TPR-FPR)
KS值小于0.2：一般认为模型的区分能力较弱
KS值在[0.2, 0.3]区间内：模型具有一定区分能力
KS值在[0.3, 0.5]区间内：模型具有较强的区分能力
KS过大（如大于0.75）：往往表示模型有异常

2、回归问题常用评估指标

回归问题是机器学习领域最常见的大类问题，很多场景都可以规划到回归问题的解决范畴。回归问题的常用评估指标有很多，以下是一些常见的指标：

平均绝对误差（Mean Absolute Error, MAE）
均方误差（Mean Squared Error, MSE）
均方根误差（Root Mean Squared Error, RMSE）
决定系数（R-Squared, R²）

2.1、平均绝对误差

这个指标在计算时，先对真实值与预测值的距离（橙色线段长度）求和，再取平均值，值越小，模型越好。

$MAE = \frac{1}{m}\sum_{i=1}^{m}|f(x_{i})-y_{i}|$

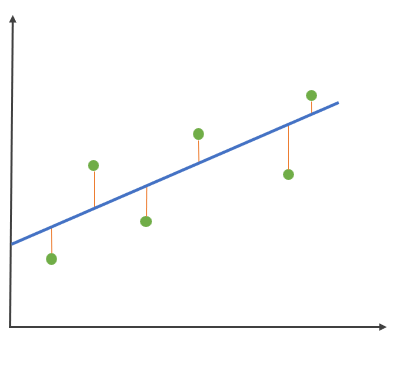
其中:

$f(x_{i})$ ：预测值
$y_{i}$ ：真实值
m ：数据量

平均绝对误差可以准确地反映实际预测误差的大小，但是，MAE 有个致命的缺点。我们现在把左边的 Y 轴缩小 1000 倍，也就是从 1000 -> 1，接下来，计算 MAE：

数据集范围大会计算获得较大的 MAE
数据集范围小会计算获得较小的 MAE

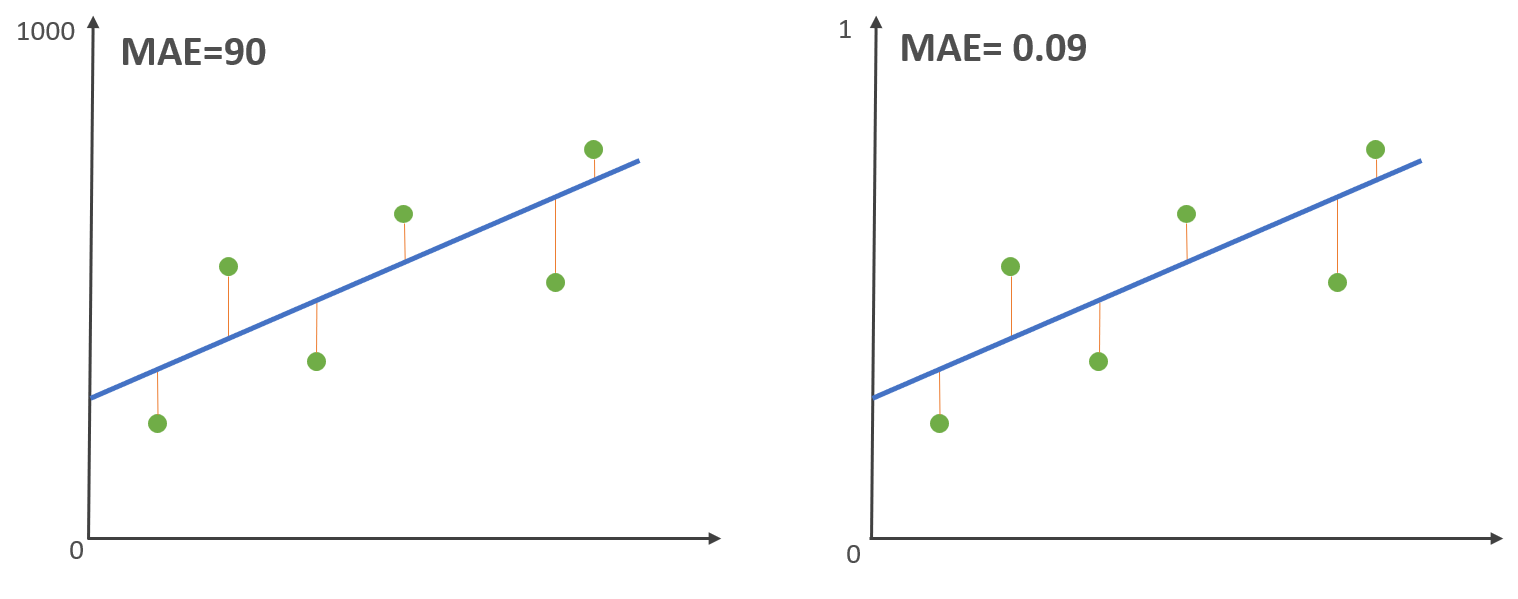
可以看到，回归模型拟合没有变化，但是MAE 会随着数据的范围有较大的变化，也就说 MAE 指标不能显示回归模型拟合是优还是劣。

2.2、均方误差 MSE

现在对平均绝对误差求平方根，就能得到均方误差（MSE）。这个指标在计算时，先对真实值与预测值的距离平方（橙色面积）后求和，再取平均值，值越小，模型越好。

$MSE = \frac{1}{m}\sum_{i=1}^{m}(f(x_{i})-y_{i})^{2}$

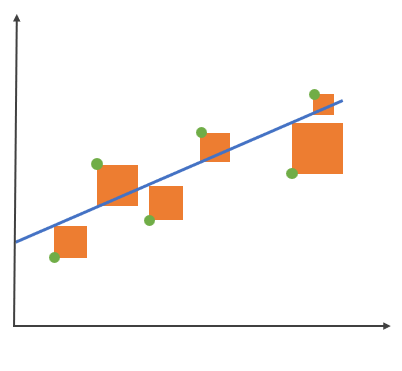
该指标避免了 MAE 的绝对值导致函数不能求导的问题，因此均方误差常用于线性回归的损失函数。另一方面，均方误差可以通过平方来放大预测偏差较大的值，提高了检测灵敏度(对异常值敏感）。

2.3、均方根误差RMSE

均方根误差，也称标准误差，是在均方误差的基础上进行开方运算，常用于衡量观测值与真实值间的偏差。

$RMSE = \sqrt{MSE} =\sqrt{\frac{1}{m}\sum_{i=1}^{m}(f(x_{i})-y_{i})^{2}}$

MAE、MSE，RMSE 都会计算均值，它可以消除样本数量对评价指标的影响，使得评估指标的大小不会太依赖于样本数量，而是更多地反映模型的误差。

2.4、决定系数R2

该指标需要了解另外三个指标：

SSR(Sum of Squares of the Regression)

计算预测数据与真实数据均值之差的平方和，反映的是模型数据相对真实数据均值的离散程度。

$SSR = \sum_{i=1}^{m}(f(x_{i}) - \bar{y})^{2}$

SST(Total Sum of Squares)

计算真实数据和其均值之差的平方和，反映的是真实数据相对均值的离散程度。

$SST = \sum_{i=1}^{m}(y_{i} - \bar{y})^{2}$

SSE(Sum of Squares for Error)

真实数据和预测数据之差的平方和

$SSE = \sum_{i=1}^{m}(f(x_{i}) - y_{i})^{2}$

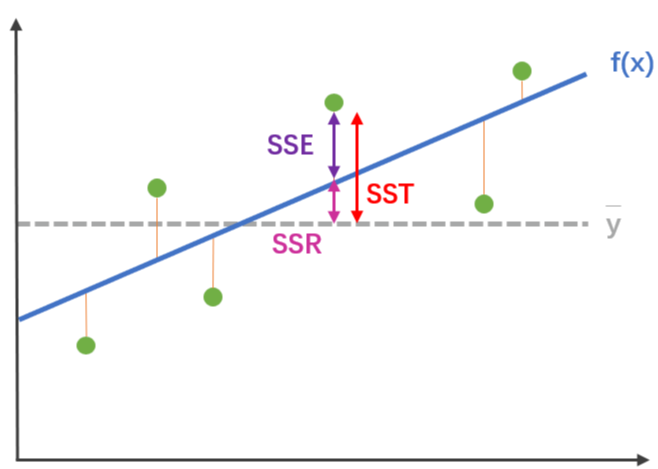
从上图我们可以注意到，SST = SSR + SSE

$R^{2} = \frac{SSR}{SST}$

决定系数R2 通过计算SSR 与 SST的比值，反应因变量 y 的全部变异能通过回归模型被自变量 x 解释的比例。比如，R2 为0.9，则表示回归关系可以解释因变量 90% 的变异。

决定系数R2越高，越接近于1，模型的拟合效果就越好
决定系数R2越接近于0，回归直线拟合效果越差

R2 虽然可以评价回归模型效果，但会随着自变量数量的不断增加而改变。

各评估指标适用场景总结：

指标	核心特点	适用场景	关注点
MAE	对异常值不敏感，解释直观	大部分通用场景，特别是当所有误差无论大小都同等重要时。业务报告的首选，因为其单位与目标变量一致，易于向非技术人员解释。	无法体现出模型对极大误差的惩罚。
MSE	对异常值非常敏感（平方放大）	模型优化和训练（如作为损失函数）。当大误差不可接受、需要被严重惩罚时（如安全临界系统）。	量纲是原单位的平方，数值上不易直接解释。
RMSE	对异常值敏感，量纲与目标变量一致	最常用和通用的指标之一。兼具MSE的数学性质和MAE的可解释性。非常适合描述模型的典型误差大小。	由于平方根，其数值会比MAE大，对大误差的惩罚介于MAE和MSE之间。
R²	无量纲，反映模型拟合优度	模型对比：比较不同模型在同一数据集上的性能。初步评估：快速了解模型解释了多大比例的数据波动。	数据本身波动很小（方差小）时，R²会很低，但这不代表模型不好。不能用于比较不同数据集上的模型。
Adjusted R²	考虑了特征数量，惩罚无用特征	特征选择和模型选择。当比较的模型特征数量不同时，使用调整后R²比R²更公平、更可靠。	计算比R²稍复杂，但现代库通常都会直接提供。

3、模型参数调优

3.1、K折交叉验证

交叉验证(Cross-Validation)的核心思想是，对原始样本数据进行切分，然后组合成为多组不同的训练集和测试集，用训练集训练模型，用测试集评估模型。某次的训练集可能是下次的测试集，故而称为交叉验证。其中K折交叉验证的应用较为广泛，其原理如下：

将原始数据集随机等分为K份，每次选取K-1份作为训练集，用剩下的1份作为测试集，得到K个模型后将这K个模型验证的结果平均作为最终的模型性能评估。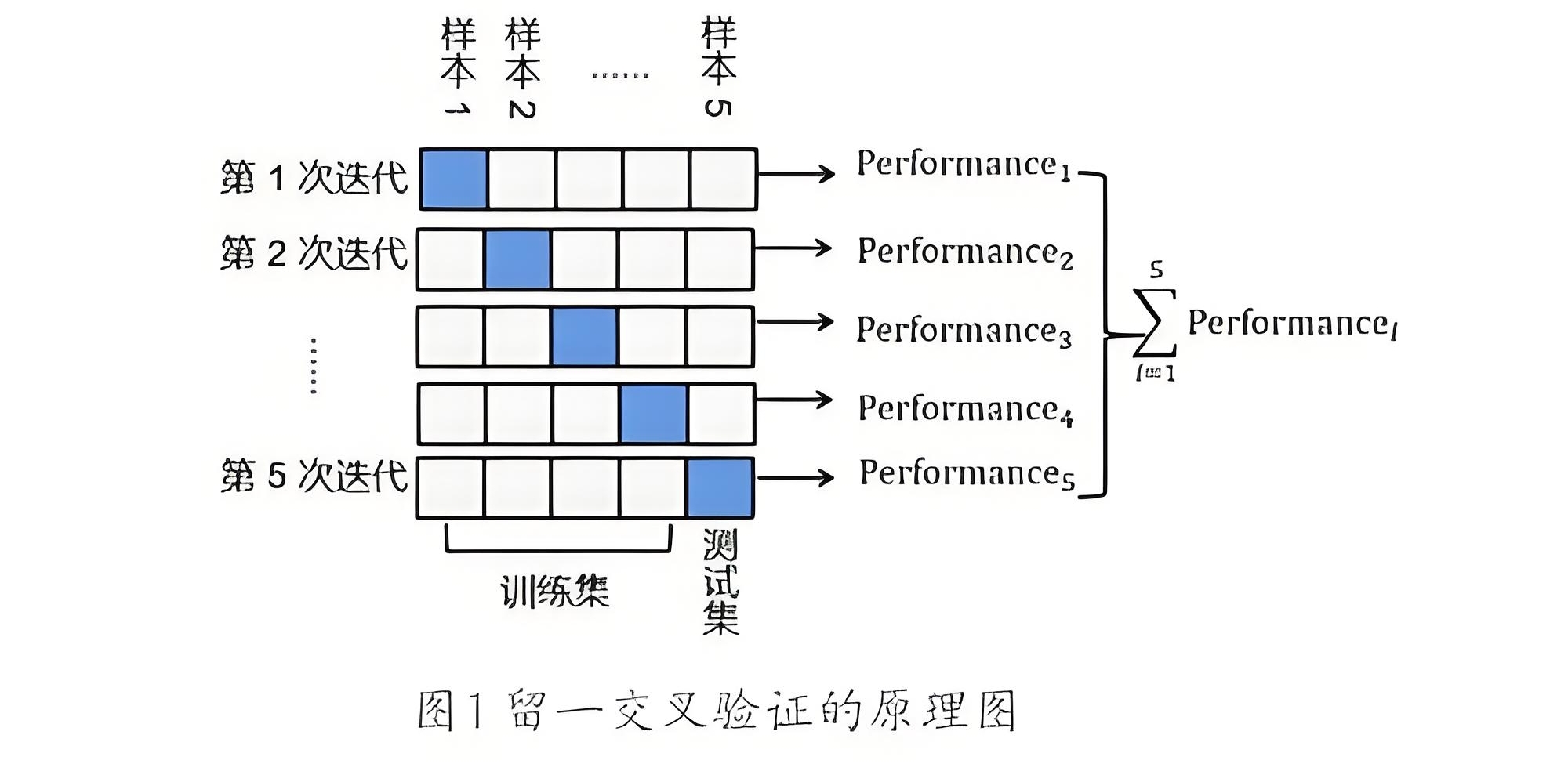

from sklearn.model_selection import cross_val_score

# model-模型名称, X-特征变量数据
# y-目标变量数据, cv-交叉验证次数
acc = cross_val_score(model, X, y, cv=5)

交叉验证可以提升模型的可信度，但不能提升模型的准确度！

3.2、GridSearch网格搜索

GridSearch网格搜索是一种穷举搜索的参数调优手段，它用于搜索模型超参数的最优组合。这种方法通过为每一个超参数定义一个搜索范围，并在这些范围内穷举所有可能的参数组合来训练模型，最后选择使得模型性能最优的参数组合。

以决策树分类模型的参数调优为例，使用网格搜索调优的实现代码如下：

from sklearn.model_selection import GridSearchCV
from sklearn.tree import DecisionTreeClassifier

parameters = {'max_depth':[1,3,5,7,9]} # 制定待调优参数max_depth的候选范围
model = DecisionTreeClassifier()

grid_search = GridSearchCV( # 构建网格搜索模型
  model,      # 传入决策树模型
  parameters, # 传入候选范围
  scoring='roc_auc', # 设置模型评估标准,此处表示以ROC曲线的AUC值作为评估标准
  cv=5        #进行5折交叉验证
)

grid_search.fit(X_train, y_train) #传入测试数据并开始进行参数调优
grid_search.best_params_          #输出参数的最优值