目录
政安晨的个人主页:政安晨
欢迎 👍点赞✍评论⭐收藏
收录专栏: 政安晨的机器学习笔记
希望政安晨的博客能够对您有所裨益,如有不足之处,欢迎在评论区提出指正!
简述
这两种经典神经网络虽然都没有在现代AI应用程序中广泛使用,但两者都是现代算法的基础。
玻尔兹曼机构成了深度信念神经网络(Deep Belief Neural Network,DBNN)的基础,它是深度学习的基本算法之一。
霍普菲尔德神经网络是一种非常简单的神经网络,它具备许多特性,这些特性也是更复杂的前馈神经网络所具有的。
霍普菲尔德神经网络(Hopfield Neural Network)是一种反馈神经网络模型,于1982年由物理学家约翰·霍普菲尔德(John Hopfield)提出。它是一种无监督学习算法,用于解决模式识别和优化问题。
霍普菲尔德神经网络由一组神经元组成,这些神经元之间通过权重相连。它采用离散的时间步骤模拟神经元之间的交互。通过迭代更新神经元的状态,网络可以从给定的输入模式中恢复出对应的输出模式,并具有自组织和容错能力。
相比传统的神经网络,霍普菲尔德神经网络的训练过程非常简单,它只需要将训练模式作为网络的权重进行初始化即可。然后,通过多次迭代更新神经元的状态,网络就可以从输入模式中恢复出相应的输出模式。这一过程被称为能量最小化,通过最小化网络的能量函数来达到模式恢复的目标。
玻尔兹曼机(Boltzmann Machine)是一种随机生成的神经网络模型,于1983年由物理学家吉尔伯特·玻尔兹曼(Geoffrey Hinton)和特里·塞杰沃斯基(Terry Sejnowski)提出。它是一种无监督学习算法,通过学习数据模式来提取特征并生成新的数据。
玻尔兹曼机由一组可见层和一组隐层神经元组成,这些神经元之间的连接是全连接的。它使用了随机状态和马尔可夫链的概念,通过马尔可夫链Monte Carlo方法进行参数估计和模式生成。
玻尔兹曼机的训练过程包括两个阶段:构造阶段和学习阶段。
在构造阶段,网络通过随机设置神经元的活跃状态来生成样本数据。
在学习阶段,网络使用对比散度算法(Contrastive Divergence)进行参数的更新和学习。
玻尔兹曼机在深度学习中起到了重要的作用,它可以用于特征提取、生成模型和无监督预训练等任务。然而,由于玻尔兹曼机的训练过程相对复杂,难以在大规模数据集上进行训练,因此在实际应用中被一些更高效的模型如深度信念网络(Deep Belief Network)所取代。
(注:看本篇文章您只要有个概念即可)
霍普菲尔德神经网络
霍普菲尔德神经网络也许是最简单的神经网络,因为它是一个完全连接的单层自动关联神经网络。换言之,它只有一层,其中每个神经元都彼此相连。此外,术语“自动关联”是指神经网络在识别出模式后会返回整个模式,神经网络将补全不完整模式或失真模式。
下图展示了只有4个神经元的霍普菲尔德神经网络。四神经元网络非常方便,因为它足够小,方便可视化,且可以识别一些模式。
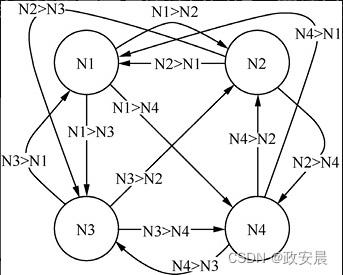
(具有12个连接的霍普菲尔德神经网络)
因为霍普菲尔德神经网络中的每个神经元都彼此相连,所以你可能会假设四神经元网络将包含4×4的矩阵,即16个连接。但是,16个连接要求每个神经元与其自身和每个其他神经元都连接。在霍普菲尔德神经网络中,不会有16个连接,其实际的连接数为12。
这些连接被加权并存储在矩阵中。4×4的矩阵将存储上图所示的网络。实际上,这个矩阵的对角线是0,因为没有自连接。本书中的所有神经网络示例都将使用某种形式的矩阵来存储其权重。
霍普菲尔德神经网络中的每个神经元的状态为真(1)或假(−1)。这些状态最初是霍普菲尔德神经网络的输入,最终成为神经网络的输出。
要确定霍普菲尔德神经元的状态是−1还是1,请使用如下公式:
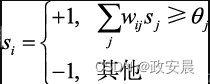
上面公式计算神经元[插图]的状态。
给定神经元的状态很大程度上取决于其他神经元的状态。该公式将其他神经元(j)的权重(w)和状态(s])相乘并进行累加。本质上,如果此总和大于阈值(θ),则当前神经元(i)的状态为+1,否则为−1。阈值通常为0。
由于单个神经元的状态取决于其他神经元的状态,因此该公式计算神经元的顺序非常重要。
程序员经常采用以下两种策略来计算霍普菲尔德神经网络中所有神经元的状态。
● 异步:这种策略一次仅更新一个神经元。它随机选择神经元。
● 同步:它同时更新所有神经元。该方法不太符合现实世界,因为生物有机体缺乏使神经元同步的全局时钟。
通常,你应该运行一个霍普菲尔德神经网络,直到所有神经元的状态稳定下来。尽管每个神经元的状态都依赖于其他神经元的状态,但神经网络通常会收敛到稳定状态。
重要的是要对神经网络收敛到稳定状态的距离有一些指标。你可以计算霍普菲尔德神经网络的能量值。随着霍普菲尔德神经网络转向更稳定的状态,该值逐步减小。
要评估神经网络的稳定性,可以使用能量函数。下面公式展示了能量函数:
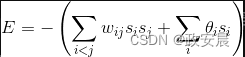
咱们后面要讨论的玻尔兹曼机也利用了这种能量函数。玻尔兹曼机与霍普菲尔德神经网络具有许多相似之处。当阈值为0时,上面公式中等号右边的第二项就会消失。下面代码清单包含实现上述公式的代码。
def energy(weights,state,threshold):
# First term
a = 0
for i in range(neuron_count):
for j in range(neuron_count):
a = a + weight[i][j] * state[i] * state[j]
a = a * -0.5
# Second term
b = 0
for i in range(neuron_count):
b = b + state[i] * threshold[i]
# Result
return a + b训练霍普菲尔德神经网络
你可以训练霍普菲尔德神经网络安排其权重,使得该神经网络收敛到所需模式(也称为训练集)。这些期望的模式是一个模式列表,对于构成玻尔兹曼机的每个神经元有一个布尔值。以下数据可能代表具有8个神经元的霍普菲尔德神经网络的一个训练集,包含4个模式:

以上数据完全是任意的。但是,它们确实代表了训练霍普菲尔德神经网络的实际模式。
训练后,类似于下面的模式应该与训练集中的一个近似的模式匹配:
1 1 1 0 0 0 0 0因此,霍普菲尔德神经网络的状态应变更为以下模式:
1 1 0 0 0 0 0 0你可以通过Hebbian或Storkey学习来训练霍普菲尔德神经网络。
Hebbian学习过程在生物学上是合理的,通常表示为“细胞如果一起激活,就连接在一起”。换言之,如果两个神经元经常对相同的输入刺激做出反应,则它们将被连接起来。下面公式从数学上总结了这种行为:
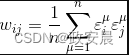
常数代表训练集元素ε(epsilon)的数量。权重矩阵是方阵,包含等于神经元数量的行和列。对角线元素总是0,因为神经元未与其自身连接。矩阵中的其他位置将包含一些值,指定训练模式中两个值是+1或−1的概率。
如下是实现上面公式的代码:
(霍普菲尔德的Hebbian训练)
def add_pattern(weights,pattern,n):
for i in range(neuron_count):
for j in range(neuron_count):
if i==j:
weights[i][j] = 0
else:
weights[i][j] = weights[i][j]
+((pattern[i] * pattern[j])/n)我们应用add_pattern方法来添加每个训练元素。参数weights指定权重矩阵,参数pattern指定每个单独的训练元素,参数n指定训练集中的元素数量。
考虑将以下数据用于训练霍普菲尔德神经网络:
[1, 0, 0, 1]
[0, 1, 1, 0]上述数据可以是如下的权重矩阵:
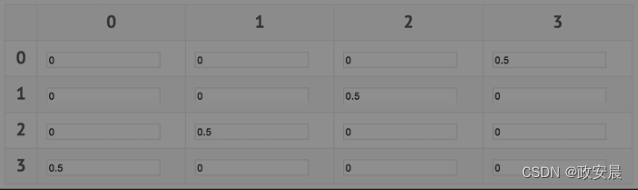
要计算上述矩阵,用1除以训练集元素的数量,结果是1/2,即0.5。值0.5放置在训练集中包含1的每个行列位置上。如第一个训练元素在神经元#0和#3中的值为1,则将0.5添加到第0行第3列和第3行第0列。对于其他训练集元素,继续执行相同的过程。
霍普菲尔德神经网络的另一种常见训练算法是Storkey算法。与刚刚描述的Hebbian算法相比,由Storkey算法训练的霍普菲尔德神经网络的模式能力更强。Storkey算法比Hebbian算法更复杂。
Hopfield-Tank神经网络
Hopfield和Tank(1984)引入了一种特殊的变体,即Hopfield-Tank神经网络,用于寻找优化问题的解。
Hopfield-Tank神经网络的结构与标准霍普菲尔德神经网络有所不同。常规霍普菲尔德神经网络中,神经元只能保存两个离散值(0或1),但是,Hopfield-Tank神经元可以保存0~1的任何数字。Hopfield-Tank神经网络可保存一个范围内的连续值。另一个重要的区别是Hopfield-Tank神经网络使用S型激活函数。
要使用Hopfield-Tank神经网络,必须创建专门的能量函数来表达要解决的每个问题的参数,但是,创建这种能量函数是一项耗时的任务。Hopfield和Tank(2008)演示了如何为旅行商问题构建能量函数。其他优化算法,如模拟退火和Nelder-Mead,不需要创建复杂的能量函数。这些通用优化算法通常比旧的Hopfield-Tank优化算法表现更好。
玻尔兹曼机
Hinton和Sejnowski(1985)首次引入了玻尔兹曼机,但是这种神经网络直到最近才得到广泛使用。受限玻尔兹曼机(Restricted Boltzmann Machine,RBM)是一种特殊的玻尔兹曼机,是深度学习和深度信念神经网络的基础技术之一。
玻尔兹曼机本质上是一个完全连接的两层神经网络。我们将这些层称为可视层和隐藏层。可视层类似于前馈神经网络中的输入层。事实上,尽管玻尔兹曼机具有隐藏层,但它更多地充当了输出层。隐藏层含义的这种差异,通常是玻尔兹曼机与前馈神经网络之间产生混淆的根源。玻尔兹曼机在输入层和输出层之间没有隐藏层。
下图展示了玻尔兹曼机的非常简单的结构。
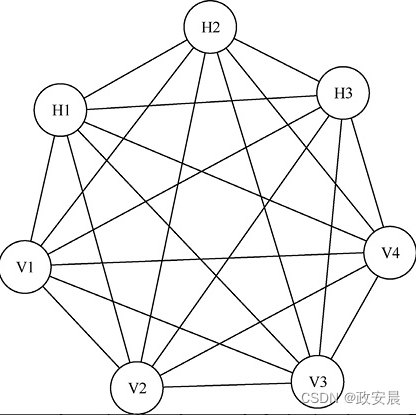
上图所示的玻尔兹曼机有3个隐藏神经元和4个可视神经元。
玻尔兹曼机是完全连接的,因为每个神经元都与其他每个神经元有连接,但是,没有神经元与其自身连接。这种连接性区分了玻尔兹曼机与受限玻尔兹曼机,如下图所示。
(受限玻尔兹曼机)
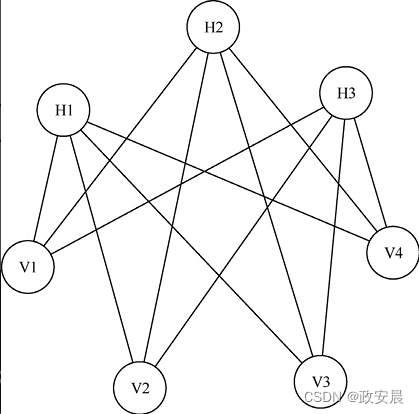
下图所示的受限玻尔兹曼机不是完全连接的。
所有隐藏神经元都连接到每个可视神经元,但是,隐藏神经元之间没有连接,可视神经元之间也没有连接。
与霍普菲尔德神经网络一样,玻尔兹曼机的神经元只能取0或1的二元值。尽管有一些关于连续玻尔兹曼机的研究,它们能够为神经元分配十进制数,但几乎所有的研究都集中在二元值的玻尔兹曼机上。
玻尔兹曼机也称为生成模型。换言之,玻尔兹曼机不会产生恒定不变的输出。提供给玻尔兹曼机的可视神经元的值,在考虑到权重后,指定了隐藏神经元将取值为1(而不是0)的概率。
尽管玻尔兹曼机和霍普菲尔德神经网络具有一些共同的特征,但仍存在一些重要差异。
● 霍普菲尔德神经网络受到识别某些错误模式的困扰;
● 玻尔兹曼机的存储模式容量可以比霍普菲尔德神经网络更大;
● 霍普菲尔德神经网络要求输入模式不相关;
● 玻尔兹曼机可以堆叠形成多层。
总之
霍普菲尔德神经网络是一种简单的神经网络,可以识别模式和解决优化问题。你必须为每种需要霍普菲尔德神经网络解决的优化问题创建特殊的能量函数。
基于这种特点,程序员会选择Nelder-Mead或模拟退火之类的算法,而不是霍普菲尔德神经网络的优化版本。
玻尔兹曼机是一种神经网络架构,它与霍普菲尔德神经网络有许多共同的特征。但是,与霍普菲尔德神经网络不同,你可以利用玻尔兹曼机堆叠深度信念神经网络。
这种堆叠能力使玻尔兹曼机在实现深度信念神经网络方面发挥了核心作用,这是深度学习的基础。


























 1633
1633

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










