有限元学习一

基于python的一维杆单元

近来想重新学习下有限元，打算第一步使用python把基础的有限元代码实现一遍，基于的教材是 Carlos A. Felippa的《INTRODUCTION to FINITE ELEMENT METHODS》

问题如下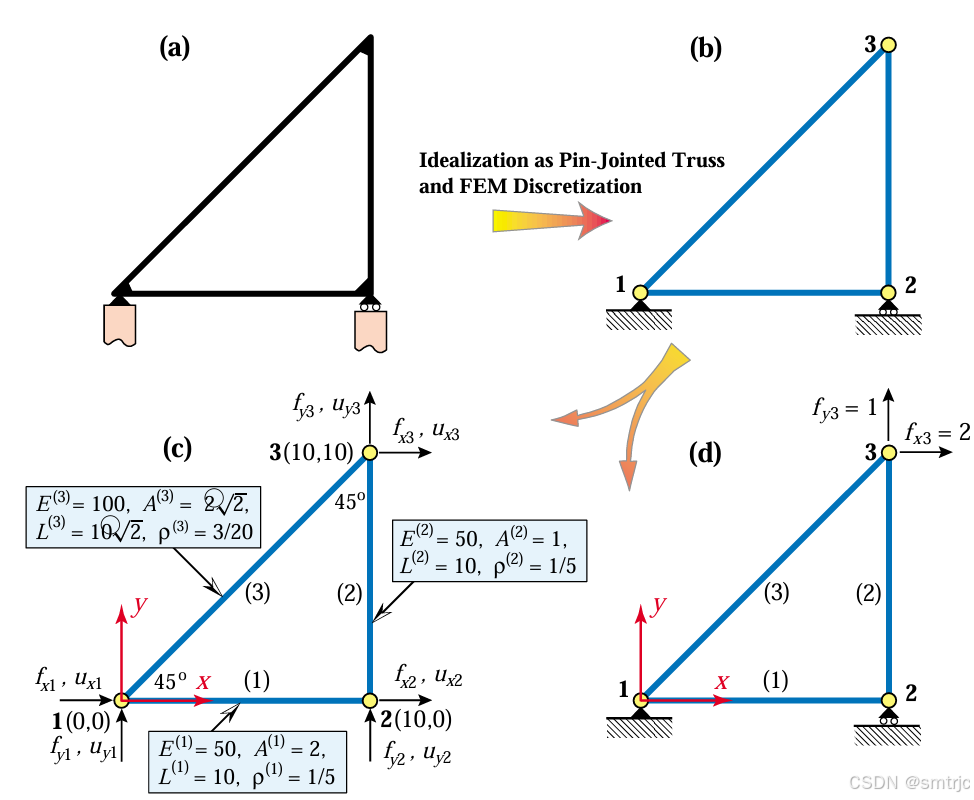

import numpy as np

class Node_coord:
    def __init__(self,x,y):
        self.x=x
        self.y=y

class Truss_ele:
    def __init__(self,node_1,node_2,numbering_1,numbering_2,E,A):
        self.numbering_1,self.numbering_2=numbering_1,numbering_2
        self.E,self.A=E,A
        self.dx,self.dy = node_2.x - node_1.x,node_2.y - node_1.y
        self.L=np.sqrt(self.dx**2+self.dy**2)
        c,s=self.dx/self.L,self.dy/self.L
        self.global_numbering=[self.numbering_1 * 2 - 2, self.numbering_1 * 2 - 1, self.numbering_2 * 2 - 2,
                            self.numbering_2 * 2 - 1]
        self.T_matrix=np.array([[c*c,s*c,-c*c,-s*c],
                                [s*c,s*s,-s*c,-s*s],
                                [-c*c,-s*c,c*c,s*c],
                                [-s*c,-s*s,s*c,s*s]])
        self.ele_matrix = self.ele_matrix_in_global_system()


    def ele_matrix_in_global_system(self):
       ele_matrix=(self.E*self.A/self.L)*self.T_matrix
       ele_matrix[np.abs(ele_matrix) < 1e-6] = 0
       return ele_matrix

    def trussIntForce(self,disp):
        disp_global_coor=disp[np.ix_(self.global_numbering)]
        c, s = self.dx / self.L, self.dy / self.L
        self.T = np.array([[c , s , 0, 0],
                           [-s, c, 0, 0],
                           [0, 0, c , s ],
                           [0, 0, -s , c]])
        disp_local=np.matmul(self.T,disp_global_coor)
        return self.E*self.A*(disp_local[2]-disp_local[0])/self.L

def global_matrix_assembly(truss_ele,global_stiffness_matrix):
    for i in range(4):
        for j in range(4):
            global_stiffness_matrix[truss_ele.global_numbering[i],truss_ele.global_numbering[j]]+=truss_ele.ele_matrix[i][j]
    return global_stiffness_matrix

def solution(U,F,K):
    active_dof = np.where(np.isnan(U))[0]
    U_unknown = np.linalg.solve(K[np.ix_(active_dof, active_dof)], F[active_dof])
    U[active_dof] = U_unknown
    return U


if __name__ == '__main__':
    nodes_total=3
    global_stiffness_matrix = np.zeros((nodes_total * 2, nodes_total * 2))

    ele1=Truss_ele(Node_coord(0,0),Node_coord(10,0),1,2,50,2)
    ele2 = Truss_ele(Node_coord(10, 0), Node_coord(10, 10), 2,3,50, 1)
    ele3 = Truss_ele(Node_coord(10, 10), Node_coord(0, 0), 3,1,100, 2**1.5)
    elems=[ele1,ele2,ele3]

    for truss in elems:
        global_stiffness_matrix=global_matrix_assembly(truss,global_stiffness_matrix)

    global_stiffness_matrix[np.abs(global_stiffness_matrix) < 1e-6] = 0

    U = np.array([0, 0, np.nan, 0, np.nan, np.nan])
    F = np.array([np.nan, np.nan, 0, np.nan, 2, 1])

    disp=solution(U,F,global_stiffness_matrix)

    inter_force=ele2.trussIntForce(disp)
    print(f"inter_force={inter_force}")
    print(f"The displacement is {disp}")