文章目录
前言
树这种数据结构天生就带有套娃的属性在,因此递归的算法在树里面应用非常广泛。另外,实际问题中,树结构非常常见,是我们必须要十分熟练的一类数据结构,也是一个练习递归算法例子最多的一章。总之,怎么强调树这种数据结构都不为过。
一、二叉树
二叉树(binary tree)是一种非线性数据结构,代表“祖先”与“后代”之间的派生关系,体现了“一分为二”的分治逻辑。与链表类似,二叉树的基本单元是节点,每个节点包含值、左子节点引用和右子节点引用。
class TreeNode:
"""二叉树节点类"""
def __init__(self, val: int):
self.val: int = val # 节点值
self.left: TreeNode | None = None # 左子节点引用
self.right: TreeNode | None = None # 右子节点引用
【注】:| 的typing要10以上Python才支持,以下版本可以采用Union[TreeNode, None]
每个节点都有两个引用(指针),分别指向左子节点(left-child node)和右子节点(right-child node),该节点被称为这两个子节点的父节点(parent node)。当给定一个二叉树的节点时,我们将该节点的左子节点及其以下节点形成的树称为该节点的左子树(left subtree),同理可得右子树(right subtree)。
在二叉树中,除叶节点外,其他所有节点都包含子节点和非空子树。如下图所示,如果将“节点 2”视为父节点,则其左子节点和右子节点分别是“节点 4”和“节点 5”,左子树是“节点 4 及其以下节点形成的树”,右子树是“节点 5 及其以下节点形成的树”。

1 二叉树常用术语
二叉树的常用术语如下图所示。
- 根节点(root node):位于二叉树顶层的节点,没有父节点。
- 叶节点(leaf node):没有子节点的节点,其两个指针均指向 None 。
- 边(edge):连接两个节点的线段,即节点引用(指针)。
- 节点所在的层(level):从顶至底递增,根节点所在层为 1 。
- 节点的度(degree):节点的子节点的数量。在二叉树中,度的取值范围是 0、1、2 。
- 二叉树的高度(height):从根节点到最远叶节点所经过的边的数量。
- 节点的深度(depth):从根节点到该节点所经过的边的数量。
- 节点的高度(height):从距离该节点最远的叶节点到该节点所经过的边的数量。

【注】:记住高度是从下往上,深度是从上往下。
【注】:请注意,我们通常将“高度”和“深度”定义为“经过的边的数量”,但有些题目或教材可能会将其定义为“经过的节点的数量”。在这种情况下,高度和深度都需要加 1 。
2 二叉树基本操作
(1)初始化二叉树
与链表类似,首先初始化节点,然后构建引用(指针)。
# 初始化二叉树
# 初始化节点
n1 = TreeNode(val=1)
n2 = TreeNode(val=2)
n3 = TreeNode(val=3)
n4 = TreeNode(val=4)
n5 = TreeNode(val=5)
# 构建节点之间的引用(指针)
n1.left = n2
n1.right = n3
n2.left = n4
n2.right = n5
(2)插入与删除节点
与链表类似,在二叉树中插入与删除节点可以通过修改指针来实现。下图给出了一个示例。

# 插入与删除节点
p = TreeNode(0)
# 在 n1 -> n2 中间插入节点 P
n1.left = p
p.left = n2
# 删除节点 P
n1.left = n2
【注】:需要注意的是,插入节点可能会改变二叉树的原有逻辑结构,而删除节点通常意味着删除该节点及其所有子树。因此,在二叉树中,插入与删除通常是由一套操作配合完成的,以实现有实际意义的操作。
3 常见二叉树类型
(1)完美二叉树(满二叉树)
完美二叉树(perfect binary tree)所有层的节点都被完全填满。在完美二叉树中,叶节点的度为 0 0 0 ,其余所有节点的度都为 2 2 2 ;若树的高度为 h h h,则节点总数为 2 h + 1 − 1 2^{h+1}-1 2h+1−1,呈现标准的指数级关系,反映了自然界中常见的细胞分裂现象。

(2)完全二叉树
完全二叉树(complete binary tree)只有最底层的节点未被填满,且最底层节点尽量靠左填充。

特别注意:如果遇到一个结点,左孩子为空,右孩子不为空,则该树一定不是完全二叉树;
也就是说最底层节点左侧要是满的才行。像下图这种就不能算是完全二叉树了

(3)完满二叉树
完满二叉树(full binary tree)除了叶节点之外,其余所有节点都有两个子节点。

(4)平衡二叉树
平衡二叉树(balanced binary tree)中任意节点的左子树和右子树的高度之差的绝对值不超过 1 。
- | 左子树高度 - 右子树高度 | <= 1

4 二叉树的退化
下图展示了二叉树的理想结构与退化结构。当二叉树的每层节点都被填满时,达到“完美二叉树”;而当所有节点都偏向一侧时,二叉树退化为“链表”。
- 完美二叉树是理想情况,可以充分发挥二叉树“分治”的优势。
- 链表则是另一个极端,各项操作都变为线性操作,时间复杂度退化至 O ( n ) O(n) O(n)。

如下表所示,在最佳结构和最差结构下,二叉树的叶节点数量、节点总数、高度等达到极大值或极小值。
| 完美二叉树 | 链表 | |
|---|---|---|
| 第 i i i层节点数量 | 2 i − 1 2^i-1 2i−1 | 1 |
| 高度为 h h h的树的叶节点数量 | 2 h 2^h 2h | 1 |
| 高度为 h h h的树的节点总数 | 2 h + 1 − 1 2^{h+1}-1 2h+1−1 | h + 1 h+1 h+1 |
| 节点总数为 n n n的树的高度 | l o g 2 ( n + 1 ) − 1 log_2(n+1)-1 log2(n+1)−1 | n − 1 n-1 n−1 |
5 二叉树的遍历
从物理结构的角度来看,树是一种基于链表的数据结构,因此其遍历方式是通过指针逐个访问节点。然而,树是一种非线性数据结构,这使得遍历树比遍历链表更加复杂,需要借助搜索算法来实现。
二叉树常见的遍历方式包括层序遍历、前序遍历、中序遍历和后序遍历等。
(1)前序、中序、后序遍历(深度优先搜索dfs)
相应地,前序、中序和后序遍历都属于深度优先遍历(depth-first traversal),也称深度优先搜索(depth-first search, DFS),它体现了一种“先走到尽头,再回溯继续”的遍历方式。
下图展示了对二叉树进行深度优先遍历的工作原理。深度优先遍历就像是绕着整棵二叉树的外围“走”一圈,在每个节点都会遇到三个位置,分别对应前序遍历、中序遍历和后序遍历。
- 前序遍历:访问优先级:根节点 -> 左子树 -> 右子树
- 中序遍历:访问优先级:左子树 -> 根节点 -> 右子树
- 后序遍历:访问优先级:左子树 -> 右子树 -> 根节点

- 遍历框架
class TreeNode:
# 二叉树经典框架
def __init__(self,val=None,left=None,right=None):
self.val = val
self.left = left
self.right = right
def dfs(root):
if not root:
return
# 前序遍历位置,进入节点的时刻
dfs(root.left)
# 中序遍历位置,节点左子树转右子树的时刻(即节点左子树已经处理完的时刻)
dfs(root.right)
# 后序遍历位置,离开节点的时刻
【注】:用这个框架就是要理解在什么时刻该干什么事情。
- 具体例子
def pre_order(root: TreeNode | None):
"""前序遍历"""
if root is None:
return
# 访问优先级:根节点 -> 左子树 -> 右子树
res.append(root.val)
pre_order(root=root.left)
pre_order(root=root.right)
def in_order(root: TreeNode | None):
"""中序遍历"""
if root is None:
return
# 访问优先级:左子树 -> 根节点 -> 右子树
in_order(root=root.left)
res.append(root.val)
in_order(root=root.right)
def post_order(root: TreeNode | None):
"""后序遍历"""
if root is None:
return
# 访问优先级:左子树 -> 右子树 -> 根节点
post_order(root=root.left)
post_order(root=root.right)
res.append(root.val)
前序遍历二叉树的递归过程,其可分为“递”和“归”两个逆向的部分。
- “递”表示开启新方法,程序在此过程中访问下一个节点。
- “归”表示函数返回,代表当前节点已经访问完毕。
【注】:这块hello算法有一个动态图(一颗递归树),可以看一下。二叉树的遍历
下面在看一下这种遍历的复杂度分析:
- 时间复杂度为 O ( n ) O(n) O(n):所有节点被访问一次,使用 O ( n ) O(n) O(n) 时间。
- 空间复杂度为 O ( n ) O(n) O(n):在最差情况下,即树退化为链表时,递归深度达到 n n n,系统占用 O ( n ) O(n) O(n)栈帧空间。
【注】:这里 n n n要理解成递归节点的个数。
(2)二叉树的层序遍历(广度优先搜索bfs)
看不懂这里有个参考视频:二叉树层序遍历参考视频
层序遍历(level-order traversal)从顶部到底部逐层遍历二叉树,并在每一层按照从左到右的顺序访问节点。
层序遍历本质上属于广度优先遍历(breadth-first traversal),也称广度优先搜索(breadth-first search, BFS),它体现了一种“一圈一圈向外扩展”的逐层遍历方式。

下面给出层序遍历的模版,并且这还是leetcode上的一道题。
102.二叉树的层序遍历

# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if not root:
return []
res = []
# 队列,尾部队尾进队,头部队首出队
queue = [root]
while queue:
# 队列为空才结束循环,其实这个也在控制遍历的层数
cur_level_size = len(queue)
level = []
for _ in range(cur_level_size):
# 遍历当前层节点个数
cur = queue.pop(0)
level.append(cur.val)
if cur.left:
queue.append(cur.left)
if cur.right:
queue.append(cur.right)
res.append(level)
return res
复杂度分析:
- 时间复杂度 O ( n ) O(n) O(n):所有节点被访问一次,使用 O ( n ) O(n) O(n)时间,其中 n n n为节点数量。
- 空间复杂度 O ( n ) O(n) O(n):在最差情况下,即满二叉树,遍历到最底层之前,队列中最多同时存在 ( n + 1 ) / 2 (n+1)/2 (n+1)/2个节点,占用 O ( n ) O(n) O(n)空间。
6 二叉树的数组表示
在链表表示下,二叉树的存储单元为节点 TreeNode ,节点之间通过指针相连接。上一节介绍了链表表示下的二叉树的各项基本操作。
我们能否用数组来表示二叉树呢?答案是肯定的。
(1)完美(满)二叉树的数组表示
先分析一个简单案例。给定一棵完美二叉树,我们将所有节点按照层序遍历的顺序存储在一个数组中,则每个节点都对应唯一的数组索引。
根据层序遍历的特性,我们可以推导出父节点索引与子节点索引之间的“映射公式”:若某节点的索引为 i i i ,则该节点的
- 左子节点索引为 2 i + 1 2i+1 2i+1
- 右子节点索引为 2 i + 2 2i+2 2i+2
下图展示了各个节点索引之间的映射关系。

映射公式的角色相当于链表中的节点引用(指针)。给定数组中的任意一个节点,我们都可以通过映射公式来访问它的左(右)子节点。
(2)任意二叉树的数组表示
完美二叉树是一个特例,在普通二叉树的中间层通常存在许多 None。没有节点的地方我们就有None在数组里面表示就可以了。
为了解决此问题,我们可以考虑在层序遍历序列中显式地写出所有 None 。如图所示,这样处理后,层序遍历序列就可以唯一表示二叉树了。示例代码如下:
# 二叉树的数组表示
# 使用 None 来表示空位
tree = [1, 2, 3, 4, None, 6, 7, 8, 9, None, None, 12, None, None, 15]

【注】:需要注意的是完全二叉树的表示可以忽略所有None
(3)完全二叉树的数组表示(在堆的那一节会用到这个)
值得说明的是,完全二叉树非常适合使用数组来表示。回顾完全二叉树的定义,None 只出现在最底层且靠右的位置,因此所有 None 一定出现在层序遍历序列的末尾。
这意味着使用数组表示完全二叉树时,可以省略存储所有 None ,非常方便。下图给出了一个例子。

7 二叉搜索树(练习递归的好案例)
参考视频:这个视频讲的很好,建议先看看这个视频
【注】:二叉搜索树里面的几种常见操作是练习递归的好案例,好好琢磨琢磨
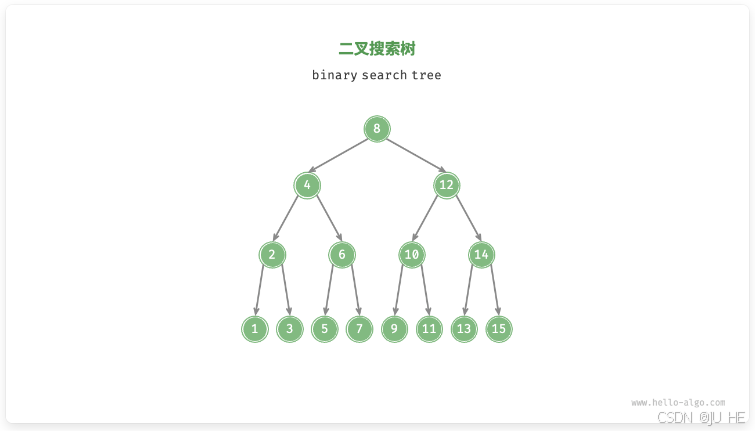
二叉搜索树(binary search tree)满足以下条件。
- 对于根节点,左子树中所有节点的值<根节点的值<右子树中所有节点的值。
- 任意节点的左、右子树也是二叉搜索树,即同样满足条件 1. 。
由于二叉搜索树的的这种性质,所以可以放心二叉搜索树的中序遍历是有序的。
这意味着在二叉搜索树中进行中序遍历时,总是会优先遍历下一个最小节点,从而得出一个重要性质:二叉搜索树的中序遍历序列是升序的。
利用中序遍历升序的性质,我们在二叉搜索树中获取有序数据仅需 O ( n ) O(n) O(n)时间,无须进行额外的排序操作,非常高效。
二叉搜索树的基本操作
【注】:下面的几种操作都会给出普通和递归两种实现版本,特别是递归版本,好好体会,是练习递归的好案例。最关键就行想清楚我最后递归结束最简单的子问题要干什么这是关键。
我们将二叉搜索树封装为一个类 BinarySearchTree ,并声明一个成员变量 root ,指向树的根节点。
【注】:本节具体操作的示意图应该是动态的,可以上hello算法查看
(1)查找节点
普通实现与递归实现:
给定目标节点值 num ,可以根据二叉搜索树的性质来查找。如图所示,我们声明一个节点 cur ,从二叉树的根节点 root 出发,循环比较节点值 cur.val 和 num 之间的大小关系。
- 若 cur.val < num ,说明目标节点在 cur 的右子树中,因此执行 cur = cur.right 。
- 若 cur.val > num ,说明目标节点在 cur 的左子树中,因此执行 cur = cur.left 。
- 若 cur.val = num ,说明找到目标节点,跳出循环并返回该节点。
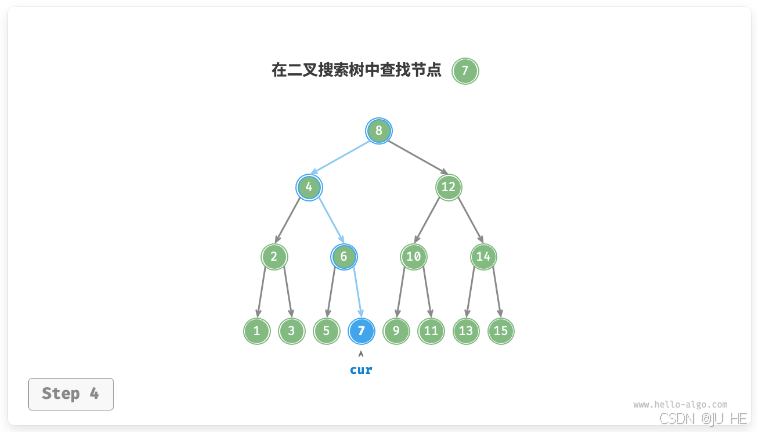
二叉搜索树的查找操作与二分查找算法的工作原理一致,都是每轮排除一半情况。循环次数最多为二叉树的高度,当二叉树平衡时,使用 O ( l o g n ) O(logn) O(logn)时间。实现代码如下:
def search(self, num: int) -> Union[TreeNode, None]:
'''
查找节点:思路1,普通思路
:param num:
:return:
'''
cur = self.root
while cur:
if cur.val == num:
return cur
if cur.val > num:
cur = cur.left
if cur.val < num:
cur = cur.right
return None
def search2(self, num: int) -> Union[TreeNode, None 二叉树与多叉树的全面解析
二叉树与多叉树的全面解析





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








