二叉搜索树、AVL以及红黑自平衡二叉搜索树-优快云博客

本文链接：https://blog.youkuaiyun.com/slx_share/article/details/82988366

本文符号意义

q: 插入节点
M: 实际删除节点(后继节点)
P: 当前节点的父节点
G: 当前节点的爷爷节点
S: 当前节点的叔叔节点(即父节点的兄弟节点)
L: 左孩子
R: 右孩子
非空：节点的key值不为空

二叉搜索树

二叉搜索树的基本操作有search(搜索)、insert(插入)、delete(删除)

搜索

key值小于当前节点，则搜索当前节点的左子树，反之右子树，直到叶节点(左右孩子不存在)。若遇到相同key则返回True。
二叉搜索树的搜索的时间复杂度最好是O(logn),但在以下两种情况下，将和线性搜索O(n)无异。

插入

搜索到叶节点，若比叶节点key小，则添加为当前叶节点的左孩子，反之右孩子。

删除

若预删除节点M不是叶节点会破坏树的性质。一种简单的方法是寻找后继节点，将后继节点存储的数据复制给预删除节点，然后删除后继节点即可。后继节点最多一个孩子节点。
分成以下几种情形讨论：

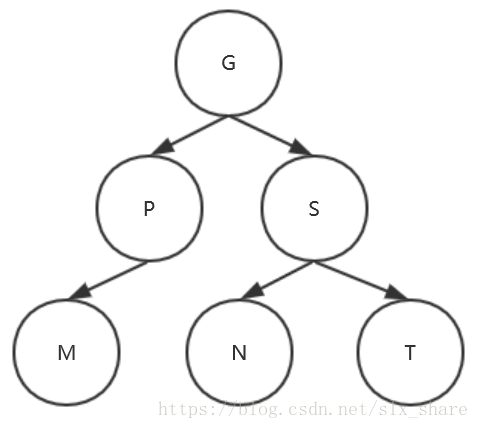
M是叶节点。无后继节点，直接删除(如图中M,N,T)
M只有左孩子。左孩子即为后继节点(如图中M就是P的后继节点)
M有右孩子。
- M的右孩子没有左孩子。右孩子就是后继节点(如图中T就是S的后继节点)
- M的右孩子有左孩子。左子树中key最小的节点就是后继节点，即最靠左的节点(只有右孩子或为叶节点)(如图中N就是G的后继节点)

# 寻找后继节点以及删除操作参考代码
def findSuccessor(self, node):
    # 找到后继节点， 即右子树中最左的节点
    currentNode = node.right.left
    while True:
        if not currentNode.hasLeft() or not currentNode.left.key:
            return currentNode
        currentNode = currentNode.left
        
def delete(self, key):
    p = self._search(key)
    if p.key != key:
        print('the {} is not on the tree'.format(key))
    else:
        if p.hasRight():
            if p.right.hasLeft():
                succ = self.findSuccessor(p)
                p.key = succ.key
                succ.parent.left = succ.right
                if succ.hasRight():
                    succ.right.parent = succ.parent
            else:
                p.key = p.right.key
                if p.right.hasRight():
                    p.right.right.parent = p
                p.right = p.right.right
        else:
            if p.hasLeft():
                p.parent.left = p.left
                p.left.parent = p.parent
            else:
                if p.isLeft():
                    p.parent.left = None
                else:
                    p.parent.right = None

自平衡二叉搜索树

AVL树以及红黑树是自平衡二叉搜索树。较二叉搜索树而言主要的差别在于为了编码方便，在每个原本意义上的叶节点下加两个key为空的节点作为新的叶节点(让空的叶节点显式存在能使对树的操作更为简便)。
自平衡二叉搜索树的基本操作与二叉搜索树相同，仅在插入和删除树中的节点的同时，加一个调节树结构的过程使之尽量左右平衡。无论是AVL树还是红黑树都需要旋转操作来调节树的结构。旋转可分为左旋转与右旋转，如图所示：

可见，旋转操作是以两个节点(node1, node2)为基准。node1是老的子树根节点，node2是node1的孩子，是新的子树根节点。当node1, node2排列成"/“则进行右旋，当排列成”\"则进行左旋。

def _leftRotate(self, oldRoot, newRoot):
    # newRoot是oldRoot的右孩子
    oldRoot.right = newRoot.left
    if newRoot.left is not None:
        newRoot.left.parent = oldRoot
    newRoot.parent = oldRoot.parent
    if oldRoot.parent is not None:
        if oldRoot.parent.left == oldRoot:  # 旧的根节点是左孩子
            oldRoot.parent.left = newRoot
        else:
            oldRoot.parent.right = newRoot
    else:
        self.root = newRoot
    oldRoot.parent = newRoot
    newRoot.left = oldRoot

def _rightRotate(self, oldRoot, newRoot):
    # newRoot是oldRoot的左孩子
    oldRoot.left = newRoot.right
    if newRoot.right is not None:
        newRoot.right.parent = oldRoot
    newRoot.parent = oldRoot.parent
    if oldRoot.parent is not None:
        if oldRoot.parent.left == oldRoot:
            oldRoot.parent.left = newRoot
        else:
            oldRoot.parent.right = newRoot
    else:
        self.root = newRoot
    oldRoot.parent = newRoot
    newRoot.right = oldRoot

对于插入与删除操作需要注意两点：
无论插入节点q还是删除节点M，都无需调节q或M的孩子的结构，因此只需以其为起点自底向上调整即可。
实际删除的节点最多只有一个非空孩子节点。

AVL树

AVL树的每个节点都有一个**平衡因子(balance factor, bf)**属性，即该节点左子树的高度减去右子树的高度(也有书籍定义右减左) 。

平衡

更新平衡因子(updateBalance)

新插入节点为右孩子，其父节点bf减1，反之加1
若父节点更新之前bf等于0， break，反之以父节点为新的当前节点继续向上更新

旋转平衡树结构(rebalance)

当节点的bf的值大于1，表明左子树过深，需要右旋以减小深度，反之若bf小于-1，表明右子树过深，需要左旋以较小深度。旋转后，以当前节点为根的子树高度不变或减小1，较小1则需要继续向上更新。
旋转后bf更新公式如下:
左旋： $n o d e 1 . b f = n o d e 1 . b f + 1 - m i n (n o d e 2 . b f, 0)$ $n o d e 2 . b f = n o d e 2 . b f + 1 + m a x (n o d e 1 . b f, 0)$
右旋： $n o d e 1 . b f = n o d e 1 . b f - 1 - m a x (n o d e 1 . b f, 0)$ $n o d e 2 . b f = n o d e 2 . b f - 1 + m i n (n o d e 1 . b f, 0)$
注：node2是node1的左孩子，进行右旋为例：

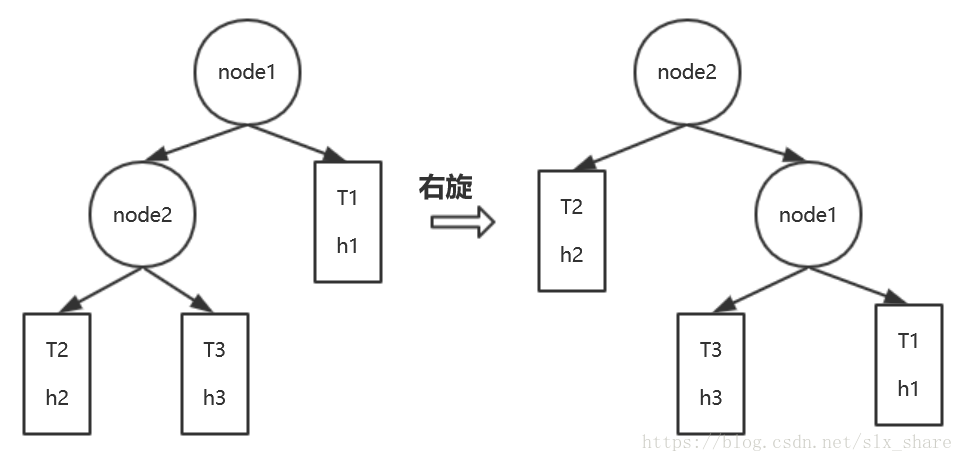
图中，T1,T2,T3表示子树。h1,h2,h3为树的高度。
旋转前： $h2-h3\qquad(1)$ $1+max(h2,h3)-h1\qquad(2)$
旋转后： $new\_node1.bf = h3-h1\qquad(3)$ $new\_node2.bf = h2 - [1+max(h3, h1)]\qquad(4)$
(3)-(2)得： $new\_node1.bf = node1.bf - 1 - max(h2-h3, 0)=node1.bf-1-max(node2.bf, 0)$
(4)-(1)得： $new\_node2.bf = node2.bf-1-max(h3-h1, 0)=node2.bf-1+min(new\_node1.bf,0)$

插入

搜索待插入叶节点q
赋予q以key值，bf设置为0，并添加空L、R孩子叶节点
以q为起点自底向上更新bf：
- 若当前节点bf小于-1或大于1，则rebalance， break(旋转后，当前节点的子树必然恢复原来的高度，故无需继续向上更新)
- 当前节点父节点不存在，break
- 父节点存在，当前节点为左孩子，父节点bf加1，反之减1
- 若父节点bf等于0，break

删除

搜索预删除节点
找到后继节点M
以M为起点自底向上更新bf：
- 若当前节点bf小于-1或大于1，则需要rebalance调整树结构，以当前节点有右孩子为例(这里与插入后调整有点区别)
  - 若右孩子平衡因子为0，则调整后树的高度是不变的，break
  - 若右孩子平衡因子为-1或1，则调整后，需要以当前节点父节点为新的当前节点
- 当前节点父节点不存在，break
- 父节点存在：
  - 父节点bf等于0，若当前节点为左孩子，bf加1，反之减1，break
  - 父节点bf不等于0，若当前节点为左孩子，bf加1，反之减1，继续向上更新
删除后继节点

# 插入和删除节点后调整bf的参考代码
def rebalanceInsert(self, currentNode):
    # 插入节点，重新调整树至平衡
    if currentNode.bf < 0:  # 左旋
        if currentNode.right.bf > 0:
            self.rightRotate(currentNode.right)
            self.leftRotate(currentNode)
        else:
            self.leftRotate(currentNode)
    elif currentNode.bf > 0:
        if currentNode.left.bf < 0:
            self.leftRotate(currentNode.left)
            self.rightRotate(currentNode)
        else:
            self.rightRotate(currentNode)

def rebalanceDelete(self, currentNode):
    # 删除节点，重新调整
    nextNode = None
    if currentNode.bf < 0:  # 右树过深，需要左旋调整
        if currentNode.right.bf < 0:
            self.leftRotate(currentNode)
            nextNode = currentNode.parent
        elif currentNode.right.bf == 0:  # 若当前节点的右孩子平衡因子为0，则旋转后以当前节点为根的子树高度不变，故结束向上更新
            self.leftRotate(currentNode)
        else:
            self.rightRotate(currentNode.right)
            self.leftRotate(currentNode)
            nextNode = currentNode.parent
    else:
        if currentNode.left.bf > 0:
            self.rightRotate(currentNode)
            nextNode = currentNode.parent
        elif currentNode.left.bf == 0:
            self.rightRotate(currentNode)
        else:
            self.leftRotate(currentNode.left)
            self.rightRotate(currentNode)
            nextNode = currentNode.parent
    return nextNode

def updateInsertBF(self, currentNode):
    # 插入节点后，更新平衡因子
    if abs(currentNode.bf) > 1:  # 树失衡则进行旋转调节
        self.rebalanceInsert(currentNode)
        return
    if currentNode.parent is not None:
        if currentNode.isLeft():
            currentNode.parent.bf += 1
        else:
            currentNode.parent.bf -= 1
        if currentNode.parent.bf != 0:
            self.updateInsertBF(currentNode.parent)

def updateDeleteBF(self, currentNode):
    # 删除节点后更新平衡因子
    if abs(currentNode.bf) > 1:  # 树失衡则进行旋转调节
        currentNode = self.rebalanceDelete(currentNode)
        if currentNode is None:
            return
    if currentNode.parent is not None:
        oldBF = currentNode.parent.bf
        if currentNode.isLeft():
            currentNode.parent.bf -= 1
        else:
            currentNode.parent.bf += 1
        if oldBF != 0:  # 父节点为根的子树，原本不平衡，那么删除节点后其子树高度必改变，故需要继续向上更新
            self.updateDeleteBF(currentNode.parent)

红黑树

红黑树的每个节点都有一个颜色(color)属性，根节点以及叶子节点(key为空)均为黑色，而其他节点满足如下两条规则：

rule1: 父子节点不能同为红色，但可以同为黑色。
rule2: 某个节点到其子树任意叶节点的路径上包含的黑色节点个数(称为black height)相同。
节点颜色的更新要以这两条准则为基础。

平衡

插入或删除后，如果树中的颜色违反了上面两条规则，则需要变更节点颜色，必要时需要旋转。过程比较复杂下面针对插入与删除的不同情形细讲。

插入

搜索到待插入叶节点q
赋予q待插入key值，标记为红色，并添加空L、R孩子叶节点
以q为起点自底向上更新color：
- q是根节点，将其标记为黑色，break
- q的父节点P是黑色，break
- q的父节点P是红色(违反rule1,需调整)：
  - q的叔叔节点S是红色，将P与S变更为黑色， break
  - S是黑色：
    - q、P以及q的爷爷节点G排列满足’/‘或’’，则以(G, P)为基准右旋或左旋，G变红色，P变黑色， break
    - q、P以及q的爷爷节点G排列满足’>‘或’<’，则以(P, q)为基准右旋或左旋，转上1

删除

搜索到待删除节点的位置
找到后继节点M，将其key复制给待删除节点
以M为起点自底向上更新color：
- M是红色，其左右孩子L和R必为空，直接删除M，break
- M是黑色：
  - L和R若存在一个非空则必为红色(参考rule2)，删除M，非空孩子接替其位置，并继承M的颜色， break
  - L和R都是空：
    - M的兄弟节点S是红色，S变黑， M的父节点P变红，再以(P,S)为基准进行旋转，转下2
    - S是黑色：
      - S的孩子全部为空：若P为黑色，则将S变红; 反之将P、S的颜色交换， break
      - S的右孩子R是红色，左孩子任意，S变红，P及R变黑，再以(P,S)为基准进行旋转，break
      - S的左孩子L是红色，L变黑，S变红，再以(S,L)为基准进行旋转，转上2

# 插入和删除节点后调整bf的参考代码
def updateInsertColor(self, currentNode):
    # 插入节点后更新颜色
    if currentNode.isRoot():
        currentNode.color = 0
        return
    elif not currentNode.parent.color:  # 父节点为黑色，不用更新
        return
    else:
        uncle = currentNode.parent.getSibling()
        if uncle.color:  # case1: 存在叔叔节点且颜色是红色
            uncle.color = 0
            currentNode.parent.color = 0
            uncle.parent.color = 1  # 将爷爷节点颜色变更为红色
            self.updateInsertColor(uncle.parent)
        else:
            if currentNode.parent.isLeft():
                if currentNode.isLeft():  # case2:当前节点、其父节点及爷爷节点位于一条直线上
                    currentNode.parent.parent.color = 1
                    currentNode.parent.color = 0
                    self.rightRotate(currentNode.parent.parent)
                else:  # case3: 当前节点、其父节点及爷爷节点不在一条直线上，先转换到一条直线上，
                    self.leftRotate(currentNode.parent)
                    self.updateInsertColor(currentNode.left)
            else:
                if currentNode.isRight():
                    currentNode.parent.parent.color = 1
                    currentNode.parent.color = 0
                    self.leftRotate(currentNode.parent.parent)
                else:
                    self.rightRotate(currentNode.parent)
                    self.updateInsertColor(currentNode.right)

def updateDeleteColor(self, currrentNode):
    # 删除节点后更新颜色
    if currrentNode.color:  # case1:M是红色，直接删除
        return
    else:
        if currrentNode.left.key:  # case2: M是黑色，子节点有个非空节点就，变为红色
            currrentNode.left.color = 0
            return
        elif currrentNode.right.key:
            currrentNode.right.color = 0
            return
        else:  # case3: M是黑色，子节点都是空节点(最复杂的情形)
            S = currrentNode.getSibling()
            if S.color:  # 1: S是红色，将其变更为黑色
                currrentNode.parent.color = 1
                S.color = 0
                if S.isLeft():
                    self.rightRotate(currrentNode.parent)
                else:
                    self.leftRotate(currrentNode.parent)
            if not (S.left.color or S.right.color):  # S没有红色孩子
                if currrentNode.parent.color:
                    currrentNode.parent.color, S.color = S.color, currrentNode.parent.color
                else:
                    S.color = 1
            elif S.right.color:  # 右孩子为红色，左孩子颜色任意
                if S.isRight():  # S的红色节点满足'\'
                    S.right.color = 0
                    S.color = currrentNode.parent.color
                    currrentNode.parent.color = 0
                    self.leftRotate(currrentNode.parent)
                else:  # S的红色节点满足'>'
                    S.left.color = 0
                    S.color = 1
                    self.rightRotate(S)
                    self.updateDeleteColor(currrentNode)
            else:
                if S.isLeft():
                    S.left.color = 0
                    S.color = currrentNode.parent.color
                    currrentNode.parent.color = 0
                    self.rightRotate(currrentNode.parent)
                else:
                    S.right.color = 0
                    S.color = 1
                    self.leftRotate(S)
                    self.updateDeleteColor(currrentNode)