[数据结构与算法] 快速排序动画及 JAVA 代码实现

目录

1. 快速排序动画

2. 快速排序 Java 实现

3. 总结

时间复杂度

空间复杂度

排序稳定性

---

1. 快速排序动画

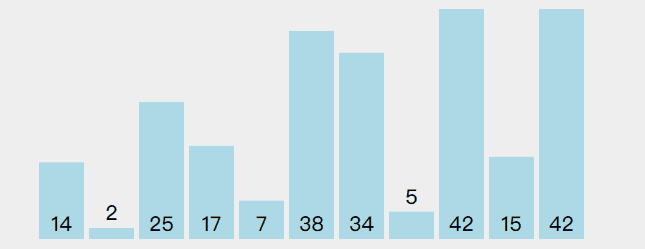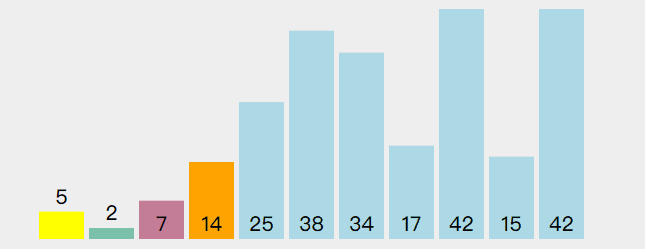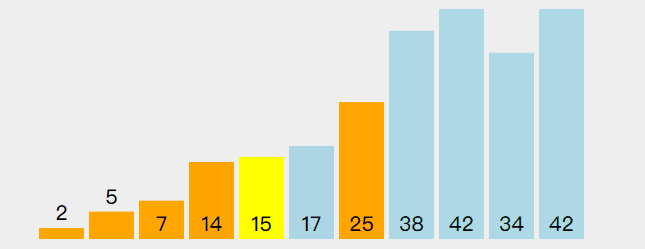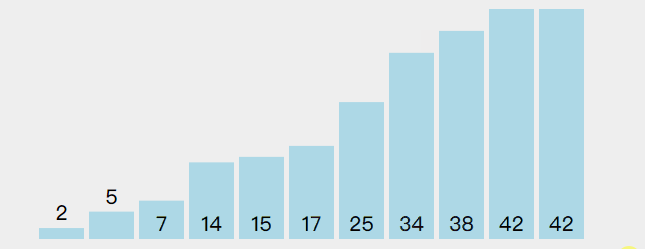
几种排序使用的同一组数据，发现这个快排动画效果不是太好

尽量看代码吧，代码 debug 下，根据数据的变化情况来帮助理解

 

2. 快速排序 Java 实现

/**
 * 快速排序
 *
 * @param numbers 待排序数组
 */
public void quickSort(int[] numbers) {
    int length = numbers.length;
    if (length <= 1) {
        return;
    }

    sort(numbers, 0, length - 1);
}

/**
 * 在排序区间段为 [left...right] 的左闭右闭区间内进行排序操作
 *
 * @param numbers 数组
 * @param left 左索引
 * @param right 右索引
 */
public void sort(int[] numbers, int left, int right) {

    if (left >= right) {
        return;
    }

    // 将区间段内第一个位置设置为分区值
    int smallIndex = left;

    // 遍历整个排序区间
    for (int i = left + 1; i < right; i++) {
        // 小于分区值的数字依次与分区值后的位置进行交换
        if (numbers[i] < numbers[left]) {
            smallIndex++;
            swap(numbers, i, smallIndex);
        }
    }
    // 将分区值与最后一个比分区值小的数据交换
    swap(numbers, left, smallIndex);

    // 将大于等于分区值的和小于分区值的分为两部分继续进行排序
    // [left...smallIndex-1] 该区间的值都小于此时的 numbers[smallIndex]
    sort(numbers, left, smallIndex - 1);
    // [smallIndex+1...right] 该区间的值都大于等于此时的 numbers[smallIndex]
    sort(numbers, smallIndex + 1, right);
}

/**
 * 交换数组中 i,j 下标对应的值
 *
 * @param numbers 数组
 * @param i 下标
 * @param j 下标
 */
public void swap(int[] numbers, int i, int j) {
    if (i == j) {
        return;
    }
    numbers[i] ^= numbers[j];
    numbers[j] ^= numbers[i];
    numbers[i] ^= numbers[j];
}

 

3. 总结

时间复杂度

极端情况下，每次分组后的两个区间数据个数都是 1:X 的情况，时间复杂度将会降为 O(n^2) 

但从整体来看快速排序时间复杂度为 O(nlogn)

 

空间复杂度

数据交换在原数组中进行，属于原地排序

但排序通过递归方式实现，每次分组后都需要记录分区值，这时候分区值的记录就不再是 O(1) 的空间复杂度

快速排序的空间复杂度为 O(logn)

 

排序稳定性

以数组 {4,1,5,3,5,2,6} 举例

• 第一轮，以第一个值 4 为分区值
  • 第一次交换数据 —>  {4,1,5,3,5,2,6}
  • 第二次交换数据 —>  {4,1,3,5,5,2,6}
  • 第三次交换数据 —>  {4,1,3,2,5,5,6}
  • 第一轮结束后状态 —>  {2,1,3,4,5,5,6}

将第一轮分区结果与原数组比较，发现两个 5 的先后顺序已经发生了改变

在排序过程中，相同数据的先后顺序发生了改变，所以快速排序是不稳定的排序