本文介绍了神经网络中利用向量化和矩阵乘法提高效率的方法，包括矩阵乘法规则、transpose的应用以及numpy中的矩阵运算，重点讲解了为何矩阵乘法在神经网络中如此关键。
文章目录
【吴恩达p56-59】
1. 为什么neural network如此高效
- neural network可以向量化，非常有效的使用矩阵乘法。
- 这一节会了解neural network的vectorization是怎么实现的。
- 将x，b都用matrix的形式表达X,B。
- dense方程就可以vectorization。
- np.matmul()是numpy里执行矩阵乘法的方法。
2. matrix multiplication（补充）
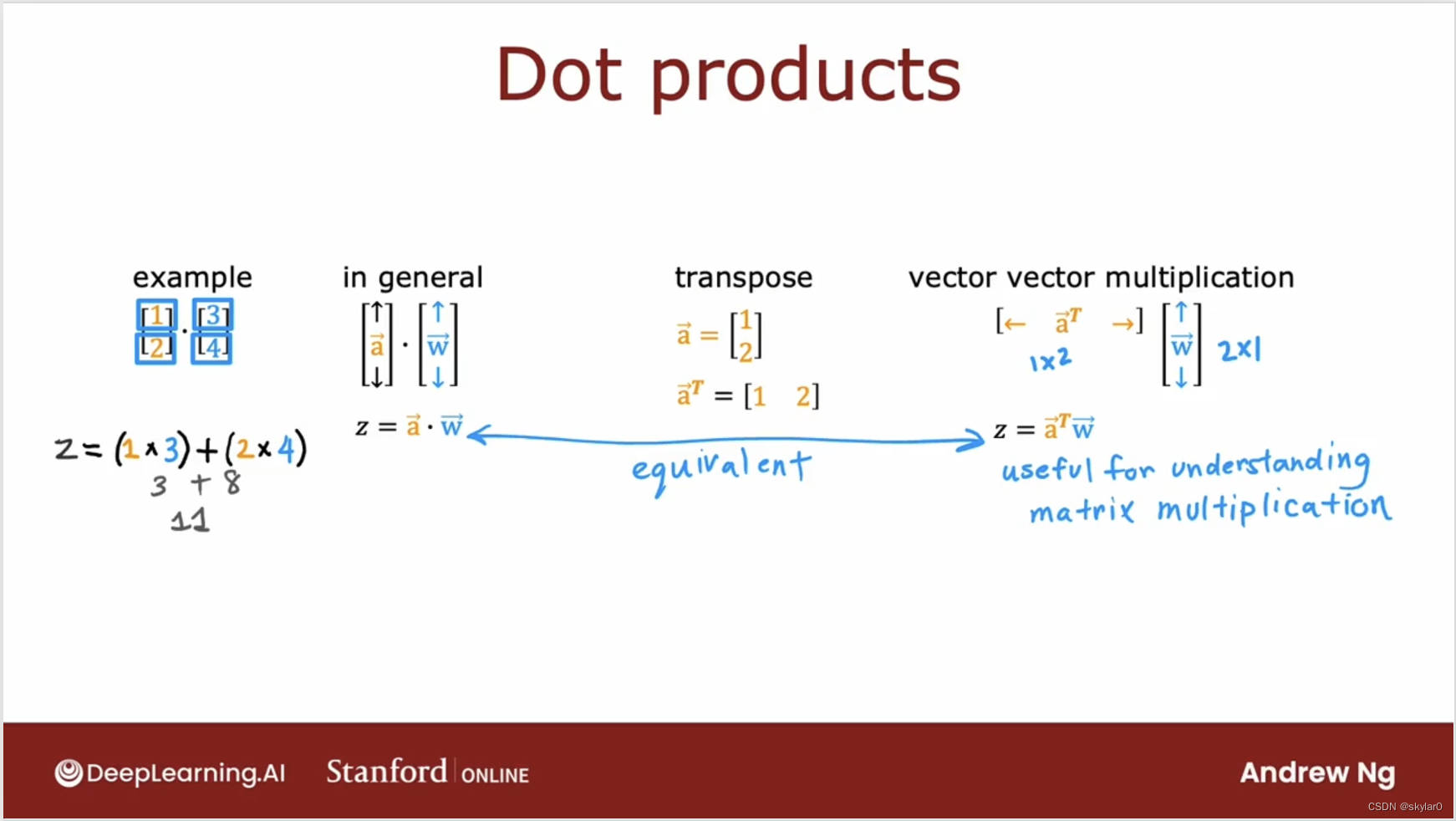
3. matrix multiplication的规则（补充）
- 将其中一个matrix做transpose（列->行）
- matrix * matrix的结果，行列的个数 = 前面matrix有几组数。
【Z=AT W，那么结果的行由AT的组数决定（3），列由W的组数决定（4）】
- 可以矩阵相乘的要求是：前一个矩阵的列数= 后一个矩阵的 行数
4. matrix multiplication的代码（optional）
- A.T表示transpose
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
