一、术语
1. 数据
数据(Data) 是信息的载体,用它来描述客观事物。
2. 元素
数据元素(Data Element)是数据的基本单位。有时,一个数据元素可以由若干个数据项组成。
3. 数据项
数据项是具有独立含义、不可再分割的最小标识单位。
如果我们把学生成绩表称为一个数据,表中的每一行就是一个数据元素,数据元素由学号、姓名、性别、课程编号、成绩等数据项组成。
术语就是大家都这么说,便于沟通,不必较真。
二、基础
1. 地址
编写代码,对数据的处理,可以简单理解为,是对内存中一个个地址对应的存储单元的读、写,地址的范围,决定了能处理多少数据。
如: 常见的32位地址,可表达 0 ~ 0xFFFFFFFF 范围的地址,即2的32次方,约4G的数据。尽管已经很大,但当前个人电脑内存常常在4G以上,更不用说服务器了,这也就是目前操作系统一般都是64位的原因。
下图演示地址与数据的关系。

2. 数据类型
a. 基础类型
例如:char, short, int, long, long long, short, double 等。
b. 结构体
它可以表达包含多个数据项的数据元素。
// 元素: 学生(学号, 姓名, 年龄)
struct Student
{
int code;
char name[20];
int age;
};c. 集合类型
它可看做是一个存储数据的容器,通常可以存储大量数据元素。
例如:线性表、栈、队列等,在三、数据结构部分会细述。
3. 变量
上面图例已叙述,变量就是给存储单元,取了一个易于理解的名字。
通过给变量定义不同的数据类型,来表明这个变量,它管理的地址范围、以及它的数据格式。
如果从存储数据的性质区分,变量可分为两类:
一类存储的是数据,例如: int a, double b, char info[20], struct Student st;
另一类存储的是地址, 即C语言的指针, 例如: int *a, struct Student *st;
三、数据结构
导读:
本部分都以学生数据(含:学号、姓名、年龄 3个数据项),进行举例说明。
1. 线性表
线性表(list)是由 n (n>=0) 个数据元素组成的有限序列。n 是线性表的长度。当n=0时,称为空表。数据表中的各元素有相同的特性。
1.1 顺序存储
特点:把线性表的元素按逻辑顺序依次存放在一组地址连续的存储单元里。
数据结构:
#define max_size 1024
// 元素: 学生(学号, 姓名, 年龄)
typedef struct
{
int code;
char name[20];
int age;
} Student;
// 数据: 学生表
typedef struct
{
Student data[max_size];
int size;
} StudentList;图示:

完整例子:
#include <stdio.h>
#define max_size 1024
// 元素: 学生(学号, 姓名, 年龄)
typedef struct
{
int code;
char name[20];
int age;
} Student;
// 数据: 学生表
typedef struct
{
Student data[max_size];
int size;
} StudentList;
// 长度
int length(StudentList *list);
// 增加
int add(StudentList *list, Student p);
// 插入
int insert(StudentList *list, Student p, int index);
// 删除
int delete(StudentList *list, int index);
// 获取
Student *get(StudentList *list, int index);
// 打印
void display(StudentList *list);
int main()
{
// 顺序表-静态初始化
StudentList sList;
sList.size = 0;
// 计算公式:sizeof(sList) = sizeof(data[max_size]) + sizeof(size) = 1024 * (4 + 20 + 4) + 4
printf("静态初始化sList, 分配空间: %d 字节\n", sizeof(sList));
// 增加元素
Student stTemp = {100, "小王100", 20};
add(&sList, stTemp);
// 等价写法
add(&sList, (Student){101, "小王101", 21});
add(&sList, (Student){102, "小王102", 22});
add(&sList, (Student){103, "小王103", 23});
add(&sList, (Student){104, "小王104", 24});
add(&sList, (Student){105, "小王105", 25});
printf("插入元素前\n");
display(&sList);
// 插入元素
insert(&sList, (Student){109, "小王109", 19}, 2);
printf("插入元素后\n");
display(&sList);
// 删除
delete (&sList, 4);
printf("删除元素后\n");
display(&sList);
// 获取
Student *st = get(&sList, 1);
printf("获取元素:index = 1\n");
printf("address=%x, code=%d, name=%s, age=%d\n", st, st->code, st->name, st->age);
printf("finish!\n");
return 0;
}
// 长度
int length(StudentList *list)
{
return list->size;
}
// 增加: 0 失败 1 成功
int add(StudentList *list, Student p)
{
// 检查: 是否已满
if (list->size == max_size)
{
printf("表已满");
return 0;
}
// 尾部追加
list->data[list->size] = p;
list->size++;
return 1;
}
// 插入: 0 失败 1 成功
int insert(StudentList *list, Student p, int index)
{
// 检查: 是否已满
if (list->size == max_size)
{
printf("表已满");
return 0;
}
// 检查: 不是插入位置
if (index >= list->size)
{
printf("插入位置错误");
return 0;
}
// 节点向后移
for (int i = list->size; i > index; i--)
{
list->data[i] = list->data[i - 1];
}
// 插入index位置
list->data[index] = p;
list->size++;
return 1;
}
// 删除
int delete(StudentList *list, int index)
{
if (index >= list->size)
{
printf("超出数据边界");
return 0;
}
// 节点向前移
for (int i = index; i < (list->size - 1); i++)
{
list->data[i] = list->data[i + 1];
}
list->size--;
return 1;
}
// 获取
Student *get(StudentList *list, int index)
{
if (index >= list->size)
{
return NULL;
}
return &(list->data[index]);
}
// 打印
void display(StudentList *list)
{
for (int i = 0; i < list->size; i++)
{
printf("address=%x, code=%d, name=%s, age=%d\n", &(list->data[i]), list->data[i].code, list->data[i].name, list->data[i].age);
}
}执行结果:
静态初始化sList, 分配空间: 28676 字节
插入元素前
address=618d30, code=100, name=小王100, age=20
address=618d4c, code=101, name=小王101, age=21
address=618d68, code=102, name=小王102, age=22
address=618d84, code=103, name=小王103, age=23
address=618da0, code=104, name=小王104, age=24
address=618dbc, code=105, name=小王105, age=25
插入元素后
address=618d30, code=100, name=小王100, age=20
address=618d4c, code=101, name=小王101, age=21
address=618d68, code=109, name=小王109, age=19
address=618d84, code=102, name=小王102, age=22
address=618da0, code=103, name=小王103, age=23
address=618dbc, code=104, name=小王104, age=24
address=618dd8, code=105, name=小王105, age=25
删除元素后
address=618d30, code=100, name=小王100, age=20
address=618d4c, code=101, name=小王101, age=21
address=618d68, code=109, name=小王109, age=19
address=618d84, code=102, name=小王102, age=22
address=618da0, code=104, name=小王104, age=24
address=618dbc, code=105, name=小王105, age=25
获取元素:index = 1
address=618d4c, code=101, name=小王101, age=21
finish!1.2 链式存储
特点:
用内存中不连续的存储单元来存储线性表的数据,链式存储结构也称为链表。
分为单向链表、双向链表、循环链表3种形式,
这里仅介绍单链表,它的每个节点,包含1个数据域 data 和 1个指针 next。
数据结构:
// 元素: 学生(学号, 姓名, 年龄)
typedef struct
{
int code;
char name[20];
int age;
} Student;
// 数据: 学生表
typedef struct Node
{
Student data;
struct Node *next;
} StudentList;图示:

完整例子:
#include <stdio.h>
#include <stdlib.h>
// 元素: 学生(学号, 姓名, 年龄)
typedef struct
{
int code;
char name[20];
int age;
} Student;
// 数据: 学生表
typedef struct Node
{
Student data;
struct Node *next;
} StudentList;
// 长度
int length(StudentList *list);
// 增加
int add(StudentList *list, Student p);
// 插入
int insert(StudentList *list, Student p, int index);
// 删除
int delete(StudentList *list, int index);
// 获取
StudentList *getNode(StudentList *list, int index);
// 打印
void display(StudentList *list);
int main()
{
// 链表表-初始化(带头节点的单链表)
StudentList sList;
sList.next = NULL;
StudentList *head = &sList;
// 计算公式:sizeof(sList) = sizeof(data) + sizeof(next) = 28 + 4 (32位环境) 或 28 + 8 (64位环境)
printf("初始化sList, 分配空间: %d 字节\n", sizeof(sList));
// 增加元素
Student stTemp = {100, "小王100", 20};
add(head, stTemp);
// 等价写法
add(head, (Student){101, "小王101", 21});
add(head, (Student){102, "小王102", 22});
add(head, (Student){103, "小王103", 23});
add(head, (Student){104, "小王104", 24});
add(head, (Student){105, "小王105", 25});
printf("插入元素前\n");
display(head);
// 插入元素
insert(head, (Student){109, "小王109", 19}, 2);
printf("插入元素后\n");
display(head);
// 删除
delete (head, 4);
printf("删除元素后\n");
display(head);
// 获取
StudentList *st = getNode(head, 1);
printf("获取元素:index = 1\n");
printf("address=%x, code=%d, name=%s, age=%d\n", st, st->data.code, st->data.name, st->data.age);
// 释放空间
int size = length(head);
for (int i = size - 1; i >= 0; i--)
{
delete (head, i);
}
printf("finish!\n");
return 0;
}
// 长度
int length(StudentList *list)
{
int result = 0;
while (list->next != NULL)
{
result++;
list = list->next;
}
return result;
}
// 增加: 0 失败 1 成功
int add(StudentList *list, Student p)
{
// 移动到尾部
while (list->next != NULL)
{
list = list->next;
}
// 动态分配空间
StudentList *newNode = (StudentList *)malloc(sizeof(StudentList));
newNode->data = p;
newNode->next = NULL;
// 加到尾部
list->next = newNode;
return 1;
}
// 插入: 0 失败 1 成功
int insert(StudentList *list, Student p, int index)
{
// 插入点的前一个节点
StudentList *prior = list;
if (index > 0)
{
prior = getNode(list, index - 1);
}
if (prior == NULL)
{
printf("插入位置错误");
return 0;
}
// 动态分配空间
StudentList *newNode = (StudentList *)malloc(sizeof(StudentList));
newNode->data = p;
// 插入链表
newNode->next = prior->next;
prior->next = newNode;
return 1;
}
// 删除
int delete(StudentList *list, int index)
{
// 删除点的前一个节点
StudentList *prior = list;
if (index > 0)
{
prior = getNode(list, index - 1);
}
if (prior == NULL || prior->next == NULL)
{
printf("删除位置错误");
return 0;
}
// 待删除节点
StudentList *delNode = prior->next;
// 从链表剔除
prior->next = delNode->next;
// 释放空间
free(delNode);
return 1;
}
// 获取节点
StudentList *getNode(StudentList *list, int index)
{
int i = 0;
while (list->next != NULL && i < index)
{
list = list->next;
i++;
}
if (i == index)
{
return list->next;
}
else
{
return NULL;
}
}
// 打印
void display(StudentList *list)
{
StudentList *p = NULL;
while (list->next != NULL)
{
p = list->next;
list = list->next;
printf("address=%x, code=%d, name=%s, age=%d\n", p, p->data.code, p->data.name, p->data.age);
}
}执行结果:
初始化sList, 分配空间: 40 字节
插入元素前
address=6e4c60, code=100, name=小王100, age=20
address=6e4cc0, code=101, name=小王101, age=21
address=6e4d20, code=102, name=小王102, age=22
address=6e4d80, code=103, name=小王103, age=23
address=6e4de0, code=104, name=小王104, age=24
address=6e4e40, code=105, name=小王105, age=25
插入元素后
address=6e4c60, code=100, name=小王100, age=20
address=6e4cc0, code=101, name=小王101, age=21
address=6e4ea0, code=109, name=小王109, age=19
address=6e4d20, code=102, name=小王102, age=22
address=6e4d80, code=103, name=小王103, age=23
address=6e4de0, code=104, name=小王104, age=24
address=6e4e40, code=105, name=小王105, age=25
删除元素后
address=6e4c60, code=100, name=小王100, age=20
address=6e4cc0, code=101, name=小王101, age=21
address=6e4ea0, code=109, name=小王109, age=19
address=6e4d20, code=102, name=小王102, age=22
address=6e4de0, code=104, name=小王104, age=24
address=6e4e40, code=105, name=小王105, age=25
获取元素:index = 1
address=6e4cc0, code=101, name=小王101, age=21
finish!1.3 顺序表 VS 链表
顺序表:
a. 它的存储空间是静态分配的,在执行之前需要明确它的存储规模。
b. 对数据的追加,按索引获取,性能都比较高,跟数据规模的大小没有关系,时间复杂度O(1)。
c. 对于数据的删除、插入,需要移动数据,性能跟数据规模的大小有关系,数据越多性能越差。
链表:
a. 它的存储空间是动态分配的,不需要提前分配存储空间。
b. 在获取数据时,需要逐个查找。
c. 在插入、删除数据时,不需要移动数据,只需要修改指针指向即可。
总结:
一般来说,线性表的操作如果以查找为主,采用顺序存储结构较好,如果以插入、删除为主,则采用链式存储结构为宜。
2. 栈
特点:
栈(stack)是限定仅在表的一端进行插入、删除操作的线性表。插入、删除的一端称为栈顶Top,
另一端称为栈底 Bottom。不含任何元素的空表称为空栈。
具体实现,可以采用顺序存储,也可以采用链式存储,下面以顺序存储为例描述。
数据结构:
#define max_size 1024
// 元素: 学生(学号, 姓名, 年龄)
typedef struct
{
int code;
char name[20];
int age;
} Student;
// 数据: 学生表
typedef struct
{
Student data[max_size];
int top;
} StudentStack;图示:
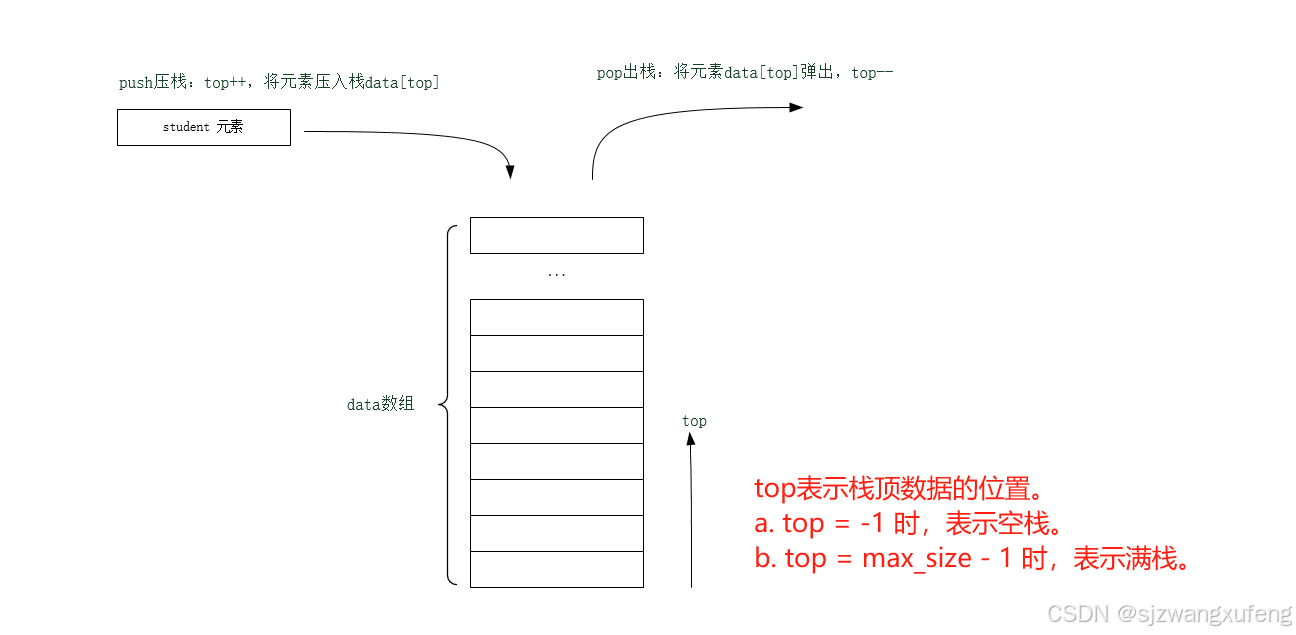
完整例子:
#include <stdio.h>
#define max_size 1024
// 元素: 学生(学号, 姓名, 年龄)
typedef struct
{
int code;
char name[20];
int age;
} Student;
// 数据: 学生表
typedef struct
{
Student data[max_size];
int top;
} StudentStack;
// 是否空栈
int isEmpty(StudentStack *stack);
// 压栈
int push(StudentStack *stack, Student p);
// 出栈
Student pop(StudentStack *stack);
int main()
{
// 栈-静态初始化
StudentStack stack;
stack.top = -1;
// 计算公式:sizeof(sList) = sizeof(data[max_size]) + sizeof(top) = 1024 * (4 + 20 + 4) + 4
printf("静态初始化stack, 分配空间: %d 字节\n", sizeof(stack));
// 压栈
push(&stack, (Student){101, "小王101", 21});
push(&stack, (Student){102, "小王102", 22});
push(&stack, (Student){103, "小王103", 23});
// 出栈
printf("\n");
while (isEmpty(&stack) == 0)
{
Student st = pop(&stack);
printf("出栈: code=%d, name=%s, age=%d\n", st.code, st.name, st.age);
}
printf("finish!\n");
return 0;
}
// 是否空栈 0 否 1 是
int isEmpty(StudentStack *stack)
{
return stack->top == -1 ? 1 : 0;
}
// 压栈
int push(StudentStack *stack, Student p)
{
// 检查: 是否已满
if (stack->top == max_size - 1)
{
printf("栈已满");
return 0;
}
printf("压栈: code=%d, name=%s, age=%d\n", p.code, p.name, p.age);
// 压栈
stack->top++;
stack->data[stack->top] = p;
}
// 出栈
Student pop(StudentStack *stack)
{
// 检查: 是否已满
if (stack->top == max_size - 1)
{
printf("栈已空");
return (Student){-1, "", 0};
}
else
{
// 出栈
stack->top--;
return stack->data[stack->top + 1];
}
}
执行结果:
静态初始化stack, 分配空间: 28676 字节
压栈: code=101, name=小王101, age=21
压栈: code=102, name=小王102, age=22
压栈: code=103, name=小王103, age=23
出栈: code=103, name=小王103, age=23
出栈: code=102, name=小王102, age=22
出栈: code=101, name=小王101, age=21
finish!3. 队列
特点:
也是一种操作受限的线性表,它只允许在表的一端插入,该端称为队尾Rear;在表的另一端进行删除,该端称为队头 Front。
以上描述只是语义,也就是保证删除元素的顺序,跟插入时元素的顺序是一致的,就跟排队一样,保证先排队,先出来,即经常说的“先入先出”规则。
数据结构:
#define max_size 5
// 元素: 学生(学号, 姓名, 年龄)
typedef struct
{
int code;
char name[20];
int age;
} Student;
// 数据: 学生表
typedef struct
{
Student data[max_size];
int front;
int rear;
} StudentQueue;图示:

完整例子:
#include <stdio.h>
#define max_size 5
// 元素: 学生(学号, 姓名, 年龄)
typedef struct
{
int code;
char name[20];
int age;
} Student;
// 数据: 学生表
typedef struct
{
Student data[max_size];
int front;
int rear;
} StudentQueue;
// 队列长度
int length(StudentQueue *queue);
// 入列
int push(StudentQueue *queue, Student p);
// 出列
Student pull(StudentQueue *queue);
int main()
{
// 队列-静态初始化
StudentQueue queue;
queue.front = 0;
queue.rear = 0;
// 入队列
printf("\n第1批数据\n");
push(&queue, (Student){101, "小王101", 21});
push(&queue, (Student){102, "小王102", 22});
push(&queue, (Student){103, "小王103", 23});
push(&queue, (Student){104, "小王104", 24});
// 测试溢出
push(&queue, (Student){105, "小王105", 25});
// 出队列
printf("\n");
while (length(&queue) > 0)
{
Student st = pull(&queue);
printf("出队列1: code=%d, name=%s, age=%d\n", st.code, st.name, st.age);
}
printf("\n第2批数据\n");
push(&queue, (Student){105, "小王107", 25});
push(&queue, (Student){106, "小王106", 26});
push(&queue, (Student){107, "小王107", 27});
// 出队列
printf("\n");
while (length(&queue) > 0)
{
Student st = pull(&queue);
printf("出队列2: code=%d, name=%s, age=%d\n", st.code, st.name, st.age);
}
printf("\n队列: front=%d, rear=%d\n", queue.front, queue.rear);
printf("finish!\n");
return 0;
}
// 队列长度
int length(StudentQueue *queue) {
return queue->rear >= queue->front ? queue->rear - queue->front : queue->rear + max_size - queue->front;
}
// 入队列
int push(StudentQueue *queue, Student p) {
int len = length(queue);
if (len == (max_size - 1)) {
printf("队列已满\n");
return 0;
}
printf("入队列: code=%d, name=%s, age=%d\n", p.code, p.name, p.age);
// 压入数据
queue->data[queue->rear] = p;
// 调整 front
queue->rear++;
if (queue->rear == max_size) {
queue->rear = 0;
}
return 1;
}
// 出队列
Student pull(StudentQueue *queue) {
int len = length(queue);
if (len == 0) {
printf("队列位空");
return (Student){-1, "", 0};
}
// 拉出数据
Student *result = &(queue->data[queue->front]);
// 调整 front
queue->front++;
if (queue->front == max_size) {
queue->front = 0;
}
return *result;
}
执行结果:
第1批数据
入队列: code=101, name=小王101, age=21
入队列: code=102, name=小王102, age=22
入队列: code=103, name=小王103, age=23
入队列: code=104, name=小王104, age=24
队列已满
出队列1: code=101, name=小王101, age=21
出队列1: code=102, name=小王102, age=22
出队列1: code=103, name=小王103, age=23
出队列1: code=104, name=小王104, age=24
第2批数据
入队列: code=105, name=小王107, age=25
入队列: code=106, name=小王106, age=26
入队列: code=107, name=小王107, age=27
出队列2: code=105, name=小王107, age=25
出队列2: code=106, name=小王106, age=26
出队列2: code=107, name=小王107, age=27
队列: front=2, rear=2
finish!4. 二叉树
前面说的线性表、栈和队列等数据结构都属于线性结构,其元素间的逻辑关系都呈现一对一关系。树和图属于非线性结构,其元素间的逻辑关系分别呈现一对多和多对多的关系。
树的元素之间存在明显的分支和层次关系。
4.1 树
树(Tree)是 n(n>=0)个结点的有限集合,其特点如下:
(1) 若n=0, 则称为空树。
(2) 若n>0, 有且仅有一个特定的结点称为树的根。
(3) 若n>1, 除根结点外,其余结点称为根的子树。
常用术语:
a. 结点的度:结点拥有的子树个数。
b. 叶子(终端结点): 度为0的结点。
c. 结点的层次:树中根结点的层次为1,根结点的子树的根为第2层,依次类推。
d. 树的度:树中所有结点的度的最大值。
e. 树的深度:树中结点层次的最大值。
f. 孩子:结点子树的根,称为这个结点的孩子。(文字虽有些绕口,还是很严谨的)
g. 双亲: 结点的直接上层结点,称为该结点的双亲。
图示:

4.2 二叉树(概念)
二叉树是 n(n>=0)个结点的有限集合,且树中所有结点的度不大于2。
二叉树与树的区别:
(1) 每个结点最多有2个子树。
(2) 二叉树的子树有左右之分,即便这个结点只有一个子树。
图示:
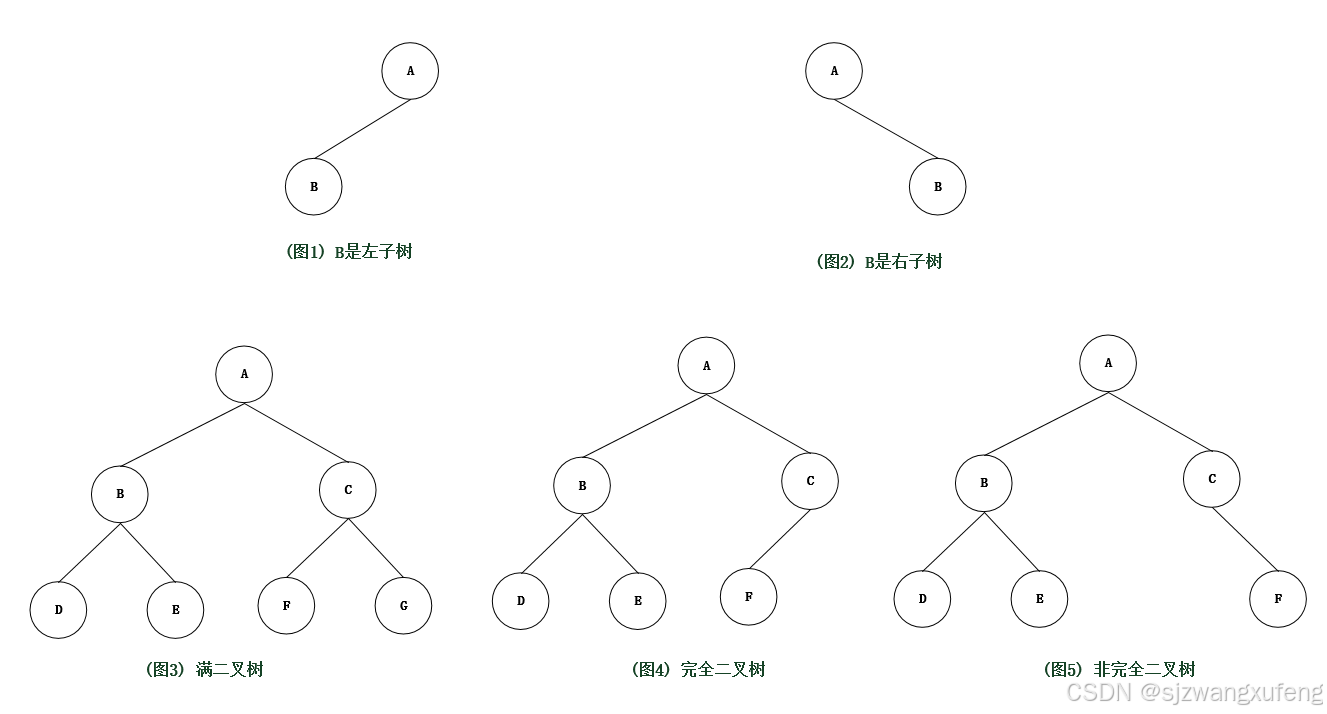
补充说明:
(1) 图1、图2 是不同的二叉树。
(2) 满二叉树:
一课深度为K,且有2的K次方-1个结点的二叉树,称为满二叉树。
特点:不存在度为1的结点,即每一层上的结点数都达到最大值。
(3) 完全二叉树:
一棵满二叉树的最下一层,从右边开始,连续删除若干个结点,所得到到二叉树,仍可称为一颗完全二叉树。
4.3 二叉树(遍历)
二叉树的遍历可分为两大类:
深度优先遍历:可以理解为先彻底遍历完一个子树,再遍历另一个,常见的有先(根)序遍历DLR、中(根)序遍历LDR、后(根)序遍历LRD。(D、L、R分别代表根、左、右)
广度优先遍历:它是按结点的层次,一层一层遍历。
以下演示深度优先遍历。
数据结构:
// 元素: 1个字符
typedef char DataType;
// 数据: 二叉树
typedef struct node
{
DataType data;
struct node *left;
struct node *right;
} BTree;图示(摘自教材,也是下面例子的数据模型)

完整例子1(递归)
#include <stdio.h>
#include <stdlib.h>
// 元素: 1个字符
typedef char DataType;
// 数据: 二叉树
typedef struct node
{
DataType data;
struct node *left;
struct node *right;
} BTree;
// 创建结点
BTree * createNode(DataType data, BTree *left, BTree *right);
// 创建用例(二叉树)
BTree * createCase();
// 遍历(先根)
void search_DLR(BTree *btree);
// 遍历(中根)
void search_LDR(BTree *btree);
// 遍历(后根)
void search_LRD(BTree *btree);
// 释放资源
void freeTree(BTree *btree);
int main()
{
// 构建二叉树(按图例)
BTree *root = createCase();
// 遍历
printf("\n\n遍历(先根)\n");
search_DLR(root);
printf("\n\n遍历(中根)\n");
search_LDR(root);
printf("\n\n遍历(后根)\n");
search_LRD(root);
// 释放资源
printf("\n\n释放资源\n");
freeTree(root);
printf("\nfinish!\n");
return 0;
}
BTree * createNode(DataType data, BTree *left, BTree *right) {
BTree *result = (BTree *) malloc(sizeof(BTree));
result->data = data;
result->left = left;
result->right = right;
return result;
}
// 创建用例(二叉树)
BTree * createCase() {
// 创建第4层
BTree *G = createNode('G', NULL, NULL);
BTree *H = createNode('H', NULL, NULL);
// 创建第3层
BTree *D = createNode('D', NULL, NULL);
BTree *E = createNode('E', NULL, G);
BTree *F = createNode('F', H, NULL);
// 创建第2层
BTree *B = createNode('B', D, E);
BTree *C = createNode('C', NULL, F);
// 创建第1层
BTree *A = createNode('A', B, C);
return A;
}
// 遍历(先根)
void search_DLR(BTree *btree) {
// 检查
if (btree == NULL) return;
// 打印
printf("%C ", btree->data);
// 左子树
search_DLR(btree->left);
// 右子树
search_DLR(btree->right);
}
// 遍历(中根)
void search_LDR(BTree *btree) {
// 检查
if (btree == NULL) return;
// 左子树
search_LDR(btree->left);
// 打印
printf("%C ", btree->data);
// 右子树
search_LDR(btree->right);
}
// 遍历(后根)
void search_LRD(BTree *btree) {
// 检查
if (btree == NULL) return;
// 左子树
search_LRD(btree->left);
// 右子树
search_LRD(btree->right);
// 打印
printf("%C ", btree->data);
}
// 释放资源
void freeTree(BTree *btree) {
// 检查
if (btree == NULL) return;
// 左子树
freeTree(btree->left);
// 右子树
freeTree(btree->right);
// 释放
btree->left = NULL;
btree->right = NULL;
printf("释放: %C\n", btree->data);
free(btree);
}
执行结果:
遍历(先根)
A B D E G C F H
遍历(中根)
D B E G A C H F
遍历(后根)
D G E B H F C A
释放资源
释放: D
释放: G
释放: E
释放: B
释放: H
释放: F
释放: C
释放: A
finish!完整例子2(非递归)
采用数组模拟栈,算法思路跟递归是类似的。
#include <stdio.h>
#include <stdlib.h>
// 元素: 1个字符
typedef char DataType;
// 数据: 二叉树
typedef struct node
{
DataType data;
struct node *left;
struct node *right;
} BTree;
// 创建结点
BTree * createNode(DataType data, BTree *left, BTree *right);
// 创建用例(二叉树)
BTree * createCase();
// 遍历(非递归)
void search(BTree *btree);
// 释放资源
void freeTree(BTree *btree);
int main()
{
// 构建二叉树(按图例)
BTree *root = createCase();
// 遍历
printf("\n\n遍历(非递归-中序)\n");
search(root);
// 释放资源
printf("\n\n释放资源\n");
freeTree(root);
printf("\nfinish!\n");
return 0;
}
BTree * createNode(DataType data, BTree *left, BTree *right) {
BTree *result = (BTree *) malloc(sizeof(BTree));
result->data = data;
result->left = left;
result->right = right;
return result;
}
// 创建用例(二叉树)
BTree * createCase() {
// 创建第4层
BTree *G = createNode('G', NULL, NULL);
BTree *H = createNode('H', NULL, NULL);
// 创建第3层
BTree *D = createNode('D', NULL, NULL);
BTree *E = createNode('E', NULL, G);
BTree *F = createNode('F', H, NULL);
// 创建第2层
BTree *B = createNode('B', D, E);
BTree *C = createNode('C', NULL, F);
// 创建第1层
BTree *A = createNode('A', B, C);
return A;
}
// 遍历(非递归)
void search(BTree *btree) {
// 提示:静态数组,树的深度不能大于 1024. (模拟栈)
BTree *stack[1024];
int stackIndex = -1;
// 遍历
BTree *p = btree;
while (p != NULL || stackIndex >= 0)
{
if (p != NULL) {
// 压栈
stackIndex++;
stack[stackIndex] = p;
// 遍历左
p = p->left;
} else {
// 出栈
p = stack[stackIndex];
stackIndex--;
// 打印
printf("%C ", p->data);
// 遍历左
p = p->right;
}
}
}
// 释放资源
void freeTree(BTree *btree) {
// 检查
if (btree == NULL) return;
// 左子树
freeTree(btree->left);
// 右子树
freeTree(btree->right);
// 释放
btree->left = NULL;
btree->right = NULL;
printf("释放: %C\n", btree->data);
free(btree);
}
执行结果:
遍历(非递归-中序)
D B E G A C H F
释放资源
释放: D
释放: G
释放: E
释放: B
释放: H
释放: F
释放: C
释放: A
finish!4.4 二叉排序树
特点:
(1) 二叉树中所有结点,如果它的左子树不为空,则左子树所有结点的值均小于该结点的值。
(2) 二叉树中所有结点,如果它的右子树不为空,则右子树所有结点的值均大于该结点的值。
上述性质,被称为二叉排序树性质(BST性质)

优点:
可以大大提高,对二叉树中结点的查找效率。
(因为它是有序的,没必要对整个二叉树进行遍历)
以图例二叉树为例:
查找"结点3“,判断路径:判断"节点6"->"节点4"->"节点2"->"节点3"
查找"结点10“,判断路径:判断"节点6"->"节点8"->"节点9",不存在。
以下2个图例都是二叉排序树,但如果查找节点,应该是高度越小,它的查找性能越高。

这就涉及一个平衡二叉树的概念,首先它是二叉排序树,且还具备以下特点:它要求树中所有结点的左右子树高度差不能超过1。(它又被称为AVL树)
4.5 二叉树、树 (互换)
任何一棵树都能转化为二叉树。
二叉树也能转化为树,但需要确保,根节点没有右孩子。
具体步骤:
第1步: 在兄弟间连线。
第2步: 保留结点与第一个孩子的连线,去掉其余的。
第3步: 以根结点为中心,将树顺时针,旋转45度,使之层次分明。
以下是教材截图:

5. 图
图是一种较复杂的非线性数据结构。图中任意两个数据元素之间均有可能相关。
因此,线性表中数据元素之间的线性关系,以及树形结构中的数据元素间的层次关系,都可以看作是图在结构上的一种简化。
5.1 定义
对于图(Graph)这种复杂的非线性数据结构,可以用两个集合V和E来表示其组成。期中V是顶点(Vertex)的非空有限集合;而E是边(Edge)的有限集合,用与表示V中任意两个顶点之间的关系集合。
从顶点间连线是否有方向,可分为:有向图、无向图。
5.2 内容
这部分还包含图的遍历、最小生成树、最短路径、拓扑排序、关键路径等,应用都很广泛。
本文只是引导入门,这部分就不再细述。
四、算法
1. 查找
在数据处理领域,查找是使用最频繁的基本操作之一。
日常生活中,通过互联网获取信息,都是查找,通过不断的优化查找(或称搜索)的性能、体验,成就了百度、谷歌等世界著名公司。
言归正传,对于数据,如果是随意的、没有规则的存储,那么对数据的查找,就只能从头到尾的遍历,再好的算法也无用武之地,数据量少还好,如果是海量的百万、亿级数据,就没法接收了。
本部分涉及的算法,前提,都默认数据是有序的。如:线性表,我们认为它是按大小排序的,二叉树,则认为它是二叉排序树。
另外,不管是有序的线性表,还是二叉排序树,在查找时,都会涉及数据的比较,为了更进一步提高查找效率,省去比较操作,人们还设计了专门的数据结构,即:哈希表(Hash)。哈希存储结构又被称为散列存储结构。
定义:在一些(有序的/无序的)数据元素中,通过一定的算法,找出与给定关键字相同的数据的过程叫做查找。
1.1 线性表
a. 顺序查找
顺序查找(Sequential Search)是一种最简单的查找,即从表头开始查找,直到找到为止。
优点: 非常明显,就是算法简单,不需要线性表是否有序。如果n很大查找效率较低,因此,顺序查找只适用于数据量小的场景。
数据结构: (其中学号是关键字)
// 元素: 学生(学号, 姓名, 年龄), 其中,学号是关键字。
typedef struct
{
int code;
char name[20];
int age;
} Student;
// 数据: 简单数组
Student students[data_size];完整例子:
#include <stdio.h>
#define data_size 10
// 元素: 学生(学号, 姓名, 年龄), 其中,学号是关键字。
typedef struct
{
int code;
char name[20];
int age;
} Student;
// 初始化模拟数据
void initData(Student arr[], int size);
// 查找: -1 表示没找到,>= 返回索引 index
int search(Student arr[], int size, int key);
int main()
{
// 数据
Student students[data_size];
initData(students, data_size);
// 打印
printf("所有学生\n");
for(int i = 0; i < data_size; i++) {
printf("code=%d, name=%s, age=%d\n", students[i].code, students[i].name, students[i].age);
}
// 查找
int code = 6;
printf("\n查找学号:%d\n", code);
int index = search(students, data_size, code);
if (index < 0) {
printf("不存在,学号:%d\n", code);
} else {
printf("结果:code=%d, name=%s, age=%d\n", students[index].code, students[index].name, students[index].age);
}
printf("\nfinish!\n");
return 0;
}
// 初始化模拟数据
void initData(Student arr[], int size) {
for (int i = 0; i < size; i++) {
arr[i].code = i + 1;
sprintf(arr[i].name, "小王%d", arr[i].code);
arr[i].age = 20 + i % 3;
}
}
// 查找
int search(Student arr[], int size, int key) {
for(int i = 0; i < size; i++) {
if (arr[i].code == key) {
return i;
}
}
return -1;
}执行结果:
所有学生
code=1, name=小王1, age=20
code=2, name=小王2, age=21
code=3, name=小王3, age=22
code=4, name=小王4, age=20
code=5, name=小王5, age=21
code=6, name=小王6, age=22
code=7, name=小王7, age=20
code=8, name=小王8, age=21
code=9, name=小王9, age=22
code=10, name=小王10, age=20
查找学号:6
结果:code=6, name=小王6, age=22
finish!b. 折半查找
折半查找(Binary Search)又称为二分查找,它是一种效率较高的查找方法。查找的对象必须是顺序存储结构的有序表。
数据结构: (其中学号是关键字)
// 元素: 学生(学号, 姓名, 年龄), 其中,学号是关键字。
typedef struct
{
int code;
char name[20];
int age;
} Student;
// 数据: 简单数组
Student students[data_size];算法图示:

完整例子:
#include <stdio.h>
#define data_size 10
// 元素: 学生(学号, 姓名, 年龄), 其中,学号是关键字。
typedef struct
{
int code;
char name[20];
int age;
} Student;
// 初始化模拟数据
void initData(Student arr[], int size);
// 查找(折半查找): 返回索引, -1 表示没找到
int search(Student arr[], int size, int key);
int main()
{
// 数据
Student students[data_size];
initData(students, data_size);
// 打印
printf("所有学生\n");
for(int i = 0; i < data_size; i++) {
printf("code=%d, name=%s, age=%d\n", students[i].code, students[i].name, students[i].age);
}
// 查找
int code = 6;
printf("\n查找学号:%d\n", code);
int index = search(students, data_size, code);
if (index < 0) {
printf("不存在,学号:%d\n", code);
} else {
printf("结果:code=%d, name=%s, age=%d\n", students[index].code, students[index].name, students[index].age);
}
printf("\nfinish!\n");
return 0;
}
// 初始化模拟数据
void initData(Student arr[], int size) {
for (int i = 0; i < size; i++) {
arr[i].code = i + 1;
sprintf(arr[i].name, "小王%d", arr[i].code);
arr[i].age = 20 + i % 3;
}
}
// 查找(折半查找): 返回索引, -1 表示没找到
int search(Student arr[], int size, int key) {
int lowIndex = 0;
int highIndex = size - 1;
int midIndex;
while (lowIndex <= highIndex) {
midIndex = (lowIndex + highIndex) / 2;
printf("比对index: %d\n", midIndex);
if (arr[midIndex].code == key) {
return midIndex;
} else if (arr[midIndex].code > key) {
highIndex = midIndex - 1;
} else {
lowIndex = midIndex + 1;
}
}
return -1;
}函数search要点分析:(需要有以下思考,训练思维的严谨性)
(1) while 会出现死循环吗?
(2) while 在最后阶段会漏数吗?
执行结果:
所有学生
code=1, name=小王1, age=20
code=2, name=小王2, age=21
code=3, name=小王3, age=22
code=4, name=小王4, age=20
code=5, name=小王5, age=21
code=6, name=小王6, age=22
code=7, name=小王7, age=20
code=8, name=小王8, age=21
code=9, name=小王9, age=22
code=10, name=小王10, age=20
查找学号:6
比对index: 4
比对index: 7
比对index: 5
结果:code=6, name=小王6, age=22
finish!c. 分块查找
分块查找(Blocking Search)又称索引顺序查找,是顺序查找的一种改进方法。该方法需要调整顺序表的结构,把一个大表,分成若干个块,每个块存储一定范围的元素,块间是有序的,数据结构包含索引表、块表,以此提高查找效率,这里不再细述。
1.2 二叉树
前面线性表讨论的算法,折半查找效率最高,但要求记录有序,且只能在顺序表(即数组)上实现,因此不适合经常需要插入、删除的大规模数据。
此时,树形结构无疑非常适合用于动态查找的数据结构,这就是数据结构部分介绍的二叉排序树和平衡二叉树,这种数据结构,不仅保证了数据的有序,也易于插入、删除操作。
图示:

数据结构:
// 元素: 1个字符
typedef int DataType;
// 数据: 二叉树
typedef struct node
{
DataType data;
struct node *left;
struct node *right;
} BTree;完整代码:
#include <stdio.h>
#include <stdlib.h>
// 元素: 1个字符
typedef int DataType;
// 数据: 二叉树
typedef struct node
{
DataType data;
struct node *left;
struct node *right;
} BTree;
// 创建结点
BTree * createNode(DataType data, BTree *left, BTree *right);
// 创建用例(二叉树)
BTree * createCase();
// 查找:返回找到的字符,0 表示没有找到
DataType find(BTree *btree, int key);
// 释放资源
void freeTree(BTree *btree);
int main()
{
// 构建二叉树(按图例)
BTree *root = createCase();
// 查找
int key = 3;
DataType result = find(root, key);
if (result == 0) {
printf("不存在, key: %d\n", key);
} else {
printf("发现, key: %d\n", key);
}
// 释放资源
//printf("\n\n释放资源\n");
freeTree(root);
printf("\nfinish!\n");
return 0;
}
BTree * createNode(DataType data, BTree *left, BTree *right) {
BTree *result = (BTree *) malloc(sizeof(BTree));
result->data = data;
result->left = left;
result->right = right;
return result;
}
// 创建用例(二叉树)
BTree * createCase() {
// 创建第4层
BTree *N1 = createNode(1, NULL, NULL);
BTree *N3 = createNode(3, NULL, NULL);
// 创建第3层
BTree *N2 = createNode(2, N1, N3);
BTree *N5 = createNode(5, NULL, NULL);
BTree *N7 = createNode(7, NULL, NULL);
BTree *N9 = createNode(9, NULL, NULL);
// 创建第2层
BTree *N4 = createNode(4, N2, N5);
BTree *N8 = createNode(8, N7, N9);
// 创建第1层
BTree *N6 = createNode(6, N4, N8);
return N6;
}
// 查找:返回找到的字符,0 表示没有找到
DataType find(BTree *btree, int key) {
// 检查
if (btree == NULL) return 0;
// 比对
printf("比对: %d \n", btree->data);
if (btree->data == key) {
return btree->data;
} else if (btree->data > key) {
// 左子树
return find(btree->left, key);
} else {
// 右子树
return find(btree->right, key);
}
return 0;
}
// 释放资源
void freeTree(BTree *btree) {
// 检查
if (btree == NULL) return;
// 左子树
freeTree(btree->left);
// 右子树
freeTree(btree->right);
//printf("释放: %d\n", btree->data);
free(btree);
}
执行结果:
比对: 6
比对: 4
比对: 2
比对: 3
发现, key: 3
finish! 如何保证二叉树,在插入、删除的过程中,始终保证有序性,其尽可能的平衡。该部分涉及一系列算法,本文不再细述。
1.3 散列表(哈希表)
散列(Hash)是一种重要的存储方法,与其他数据结构相比,它最大的特点是记录在表中的位置与关键字的值相关。换句话说,可以通过关键字直接计算出存储的位置。省去了大量的比较操作,从而提高了查找效率。
图示:

a. 初版
数据结构: (其中学号是关键字)
// 元素: 学生(学号-关键字, 姓名, 年龄)
typedef struct
{
int code;
char name[20];
int age;
} Student;
// 哈希表
Student *hash_table[max_size] = {NULL};完整例子:
#include <stdio.h>
#include <stdlib.h>
#define max_size 16
// 元素: 学生(学号, 姓名, 年龄)
typedef struct
{
int code;
char name[20];
int age;
} Student;
// 哈希表
Student *hash_table[max_size] = {NULL};
// 散列函数
int hash_number(int key);
// 保存
void hash_set(Student *p, int key);
// 获取
Student *hash_get(int key);
// 构建学生
Student *createStudent(int key);
// 释放
void freeHash();
int main()
{
// 存储
for(int i = 0; i < 20; i++)
{
int key = 100 + i;
Student *p = createStudent(key);
printf("存储: code=%d, name=%s, age=%d\n", p->code, p->name, p->age);
hash_set(p, key);
}
// 获取
printf("\n\n");
for(int i = 0; i < 20; i++)
{
int key = 100 + i;
Student *p = hash_get(key);
if (p->code == key) {
printf("正确 %d: code=%d, name=%s, age=%d\n", key, p->code, p->name, p->age);
} else {
printf("错误!!! %d: code=%d, name=%s, age=%d\n", key, p->code, p->name, p->age);
}
}
// 释放
freeHash();
printf("hello world!");
return 0;
}
// 散列函数:初六榆树法
int hash_number(int key)
{
return key % max_size;
}
// 保存
void hash_set(Student *p, int key)
{
int address = hash_number(key);
hash_table[address] = p;
}
// 获取
Student *hash_get(int key)
{
int address = hash_number(key);
return hash_table[address];
}
// 构建学生
Student *createStudent(int key)
{
Student *p = malloc(sizeof(Student));
p->code = key;
p->age = 20 + key % 10;
sprintf(p->name, "小王%d", key);
return p;
}
// 释放
void freeHash()
{
for (int i = 0; i < max_size; i++)
{
if (hash_table[i] != NULL)
{
//printf("释放: code=%d, name=%s, age=%d\n", hash_table[i]->code, hash_table[i]->name, hash_table[i]->age);
free(hash_table[i]);
}
}
};
执行结果:
存储: code=100, name=小王100, age=20
存储: code=101, name=小王101, age=21
存储: code=102, name=小王102, age=22
存储: code=103, name=小王103, age=23
存储: code=104, name=小王104, age=24
存储: code=105, name=小王105, age=25
存储: code=106, name=小王106, age=26
存储: code=107, name=小王107, age=27
存储: code=108, name=小王108, age=28
存储: code=109, name=小王109, age=29
存储: code=110, name=小王110, age=20
存储: code=111, name=小王111, age=21
存储: code=112, name=小王112, age=22
存储: code=113, name=小王113, age=23
存储: code=114, name=小王114, age=24
存储: code=115, name=小王115, age=25
存储: code=116, name=小王116, age=26
存储: code=117, name=小王117, age=27
存储: code=118, name=小王118, age=28
存储: code=119, name=小王119, age=29
错误!!! 100: code=116, name=小王116, age=26
错误!!! 101: code=117, name=小王117, age=27
错误!!! 102: code=118, name=小王118, age=28
错误!!! 103: code=119, name=小王119, age=29
正确 104: code=104, name=小王104, age=24
正确 105: code=105, name=小王105, age=25
正确 106: code=106, name=小王106, age=26
正确 107: code=107, name=小王107, age=27
正确 108: code=108, name=小王108, age=28
正确 109: code=109, name=小王109, age=29
正确 110: code=110, name=小王110, age=20
正确 111: code=111, name=小王111, age=21
正确 112: code=112, name=小王112, age=22
正确 113: code=113, name=小王113, age=23
正确 114: code=114, name=小王114, age=24
正确 115: code=115, name=小王115, age=25
正确 116: code=116, name=小王116, age=26
正确 117: code=117, name=小王117, age=27
正确 118: code=118, name=小王118, age=28
正确 119: code=119, name=小王119, age=29
hello world!b. 改进版
通过初版的运行结果,发现有些结果是错误的,这是由于不同元素关键字key,计算散列函数的address可能相同导致,这就是散列地址冲突,常见的做法是,将地址相同的元素,保存到单链表,也称为拉链法。
数据结构:
#define max_size 16
// 元素: 学生(学号, 姓名, 年龄)
typedef struct
{
int code;
char name[20];
int age;
} Student;
// 哈希点:链表
typedef struct Node
{
Student data;
struct Node *next;
} HashNode;
// 哈希表
HashNode *hash_table[max_size] = {NULL};完整例子:
#include <stdio.h>
#include <stdlib.h>
#define max_size 16
// 元素: 学生(学号, 姓名, 年龄)
typedef struct
{
int code;
char name[20];
int age;
} Student;
// 哈希点:链表
typedef struct Node
{
Student data;
struct Node *next;
} HashNode;
// 哈希表
HashNode *hash_table[max_size] = {NULL};
// 散列函数
int hash_number(int key);
// 保存
void hash_set(HashNode *p, int key);
// 获取
HashNode *hash_get(int key);
// 构建学生
HashNode *createHashNode(int key);
// 释放
void freeHash();
int main()
{
// 存储
for(int i = 0; i < 20; i++)
{
int key = 100 + i;
HashNode *p = createHashNode(key);
printf("存储: code=%d, name=%s, age=%d\n", p->data.code, p->data.name, p->data.age);
hash_set(p, key);
}
// 获取
printf("\n\n");
for(int i = 0; i < 20; i++)
{
int key = 100 + i;
HashNode *p = hash_get(key);
if(p == NULL) {
printf("不存在, key= %d\n", key);
continue;;
}
if (p->data.code == key) {
printf("正确 %d: code=%d, name=%s, age=%d\n", key, p->data.code, p->data.name, p->data.age);
} else {
printf("错误!!! %d: code=%d, name=%s, age=%d\n", key, p->data.code, p->data.name, p->data.age);
}
}
// 释放
freeHash();
printf("hello world!");
return 0;
}
// 散列函数:初六榆树法
int hash_number(int key)
{
return key % max_size;
}
// 保存
void hash_set(HashNode *p, int key)
{
int address = hash_number(key);
HashNode *head = hash_table[address];
if (head == NULL) {
hash_table[address] = p;
} else {
while (head->next != NULL)
{
head = head->next;
}
head->next = p;
}
}
// 获取
HashNode *hash_get(int key)
{
int address = hash_number(key);
HashNode *result = hash_table[address];;
while (result != NULL)
{
if (result->data.code == key) {
return result;
}
result = result->next;
}
return NULL;
}
// 构建学生
HashNode *createHashNode(int key)
{
HashNode *p = malloc(sizeof(HashNode));
p->data.code = key;
p->data.age = 20 + key % 10;
sprintf(p->data.name, "小王%d", key);
p->next = NULL;
return p;
}
// 释放
void freeHash()
{
//printf("\n释放资源\n");
for (int i = 0; i < max_size; i++)
{
if (hash_table[i] != NULL)
{
HashNode *current = hash_table[i];
HashNode *next = NULL;
do {
next = current->next;
//printf("释放: code=%d, name=%s, age=%d\n", current->data.code, current->data.name, current->data.age);
free(current);
current = next;
} while (current != NULL);
}
}
};
执行结果:
存储: code=100, name=小王100, age=20
存储: code=101, name=小王101, age=21
存储: code=102, name=小王102, age=22
存储: code=103, name=小王103, age=23
存储: code=104, name=小王104, age=24
存储: code=105, name=小王105, age=25
存储: code=106, name=小王106, age=26
存储: code=107, name=小王107, age=27
存储: code=108, name=小王108, age=28
存储: code=109, name=小王109, age=29
存储: code=110, name=小王110, age=20
存储: code=111, name=小王111, age=21
存储: code=112, name=小王112, age=22
存储: code=113, name=小王113, age=23
存储: code=114, name=小王114, age=24
存储: code=115, name=小王115, age=25
存储: code=116, name=小王116, age=26
存储: code=117, name=小王117, age=27
存储: code=118, name=小王118, age=28
存储: code=119, name=小王119, age=29
正确 100: code=100, name=小王100, age=20
正确 101: code=101, name=小王101, age=21
正确 102: code=102, name=小王102, age=22
正确 103: code=103, name=小王103, age=23
正确 104: code=104, name=小王104, age=24
正确 105: code=105, name=小王105, age=25
正确 106: code=106, name=小王106, age=26
正确 107: code=107, name=小王107, age=27
正确 108: code=108, name=小王108, age=28
正确 109: code=109, name=小王109, age=29
正确 110: code=110, name=小王110, age=20
正确 111: code=111, name=小王111, age=21
正确 112: code=112, name=小王112, age=22
正确 113: code=113, name=小王113, age=23
正确 114: code=114, name=小王114, age=24
正确 115: code=115, name=小王115, age=25
正确 116: code=116, name=小王116, age=26
正确 117: code=117, name=小王117, age=27
正确 118: code=118, name=小王118, age=28
正确 119: code=119, name=小王119, age=29
hello world!c. 影响因素
(1)散列函数
选取的散列函数,尽可能使元素均匀分布,避免频繁的冲突处理。
(2)冲突处理方法
常见的有拉链法等,以及在此基础上的变形优化。
(3)装填因子
装填因子 a = 记录数 / 散列容量;此值越大出现冲突的概率就越大。
2. 排序
排序(Sorting)是软件技术中常用的一种操作。高效的排序也是计算机程序设计的一项重要课题。
本文只介绍常见的3种排序算法:冒泡法、直接选择排序法、快速排序。其它还有希尔排序、堆排序、归并排序、基数排序等等。
另外,插一句,很多人都说,排序都有现成的类库,有必要学吗?个人认为,还是很有必要的,这些算法,有时虽不能直接解决你遇到的问题,但它开拓了你解决问题的思路,现实中哪里有标准问题、经典答案!但现实中问题的解决,都来自这些标准、经典提供的思路,哪怕是原创性的。牛顿不也说,自己是站在巨人的肩膀上吗?
2.1 直接选择排序法
直接选择排序(Straight Select Sort)又称为简单选择排序,基本思想: 每一趟从待排序记录中选出关键字最小的,依次放在已排序记录的最后,直至全部有序。
步骤:
以 int data[10] 为例。
第一趟: 从data[0] ~ data[9],找到最小放到 data[0];
第二趟: 从data[1] ~ data[9],找到最小放到 data[1];
...
第十趟,最后剩下data[9]。(因此,这一趟是没必要的)
在所有排序算法中,个人认为,它的思路最清晰、最简洁,这也是为何第一个讲的原因。
完整例子:
#include <stdio.h>
#include <stdlib.h>
#define data_size 10
// 初始化-随机数
void init_data(int data[], int size);
// 排序: 直接选择排序法
void direct_sort(int data[], int size);
// 打印
void display(int data[], int size);
int main()
{
// 初始化
int data[data_size] = {0};
init_data(data, data_size);
// 打印: 排序前
printf("排序前:\n");
display(data, data_size);
// 排序
direct_sort(data, data_size);
// 打印: 排序后
printf("排序后:\n");
display(data, data_size);
printf("\nfinish!\n");
return 0;
}
// 初始化-随机数
void init_data(int data[], int size)
{
for (int i = 0; i < size; i++)
{
data[i] = rand() % 100;
}
}
// 排序
void direct_sort(int data[], int size)
{
for (int i = 0; i < size - 1; i++)
{
int minIndex = i;
for (int j = i + 1; j < size; j++)
{
if (data[minIndex] > data[j])
{
minIndex = j;
}
}
if (i != minIndex)
{
int temp = data[i];
data[i] = data[minIndex];
data[minIndex] = temp;
}
}
}
// 打印
void display(int data[], int size)
{
for (int i = 0; i < size; i++)
{
printf("%d ", data[i]);
}
printf("\n\n");
}
执行结果:
排序前:
41 67 34 0 69 24 78 58 62 64
排序后:
0 24 34 41 58 62 64 67 69 78
finish!2.2 冒泡法
冒泡排序(Bubble Sort)是最简单和最通用的排序方法,其基本思想是:在待排序的一组数中,将相邻的两个数进行比较,若前面的数比后面的数大就交换两数,否则不交换;如此下去,直至最终完成排序。以下图示(定义、图示都来自百度百科)
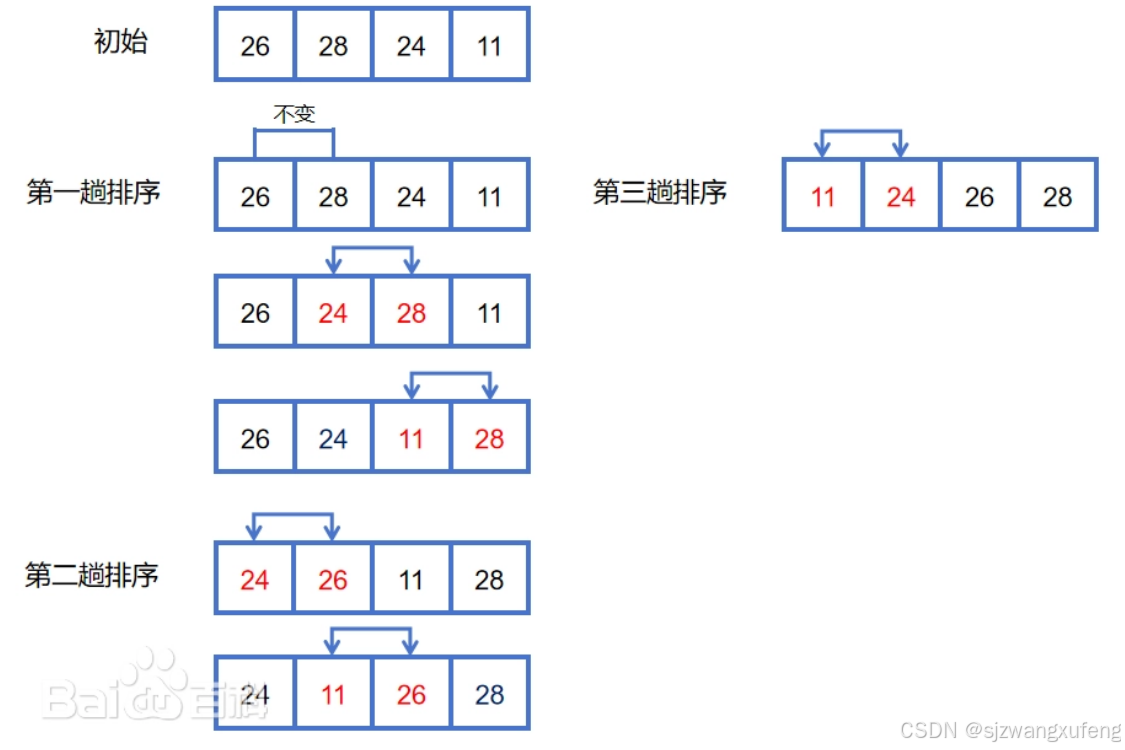
完整例子:
#include <stdio.h>
#include <stdlib.h>
#define data_size 10
// 初始化-随机数
void init_data(int data[], int size);
// 排序:冒泡法
void bubble_sort(int data[], int size);
// 打印
void display(int data[], int size);
int main()
{
// 初始化
int data[data_size] = {0};
init_data(data, data_size);
// 打印: 排序前
printf("排序前:\n");
display(data, data_size);
// 排序
bubble_sort(data, data_size);
// 打印: 排序后
printf("排序后:\n");
display(data, data_size);
printf("\nfinish!\n");
return 0;
}
// 初始化-随机数
void init_data(int data[], int size)
{
for (int i = 0; i < size; i++)
{
data[i] = rand() % 100;
}
}
// 排序
void bubble_sort(int data[], int size)
{
for (int i = 0; i < size - 1; i++)
{
for (int j = 1; j < size - i; j++)
{
if (data[j - 1] > data[j])
{
int temp = data[j - 1];
data[j - 1] = data[j];
data[j] = temp;
}
}
}
}
// 打印
void display(int data[], int size)
{
for (int i = 0; i < size; i++)
{
printf("%d ", data[i]);
}
printf("\n\n");
}
执行结果:
排序前:
41 67 34 0 69 24 78 58 62 64
排序后:
0 24 34 41 58 62 64 67 69 78
finish!2.3 快速排序
快速排序(Quick sort)是对气泡排序的一种改进,基本思想:通过一趟排序将序列分成两个子序列,然后分别对这两个子序列再进行排序,直至达到整个序列有序。
图示:

完整代码:
#include <stdio.h>
#include <stdlib.h>
#define data_size 10
// 初始化-随机数
void init_data(int data[], int size);
// 排序:快速排序
void quick_sort(int data[], int left, int right);
// 打印
void display(int data[], int size);
int main()
{
// 初始化
int data[data_size] = {0};
init_data(data, data_size);
// 打印: 排序前
printf("排序前:\n");
display(data, data_size);
// 排序
quick_sort(data, 0, data_size - 1);
// 打印: 排序后
printf("排序后:\n");
display(data, data_size);
printf("\nfinish!\n");
return 0;
}
// 初始化-随机数
void init_data(int data[], int size)
{
for (int i = 0; i < size; i++)
{
data[i] = rand() % 100;
}
}
// 排序
void quick_sort(int data[], int left, int right)
{
if (left >= right) return;
// 参考值
int ref = data[left];
int begin = left;
int end = right;
while (begin < end)
{
// 从右边开始,比 ref >= 的位置不变
while (begin < end && data[end] >= ref)
{
end--;
}
data[begin] = data[end];
// 从左边开始,比 ref <= 的位置不变
while (begin < end && data[begin] <= ref)
{
begin++;
}
data[end] = data[begin];
}
printf("分界点, begin=%d, end=%d\n", begin, end);
data[end] = ref;
// 参考值:左侧
quick_sort(data, left, begin - 1);
// 参考值:右侧
quick_sort(data, begin + 1, right);
}
// 打印
void display(int data[], int size)
{
for (int i = 0; i < size; i++)
{
printf("%d ", data[i]);
}
printf("\n\n");
}
执行结果:
排序前:
41 67 34 0 69 24 78 58 62 64
分界点, begin=3, end=3
分界点, begin=1, end=1
分界点, begin=8, end=8
分界点, begin=6, end=6
分界点, begin=4, end=4
排序后:
0 24 34 41 58 62 64 67 69 78
finish!五、算法评估
1. 时间复杂度
算法的时间复杂度,也就是算法的时间量度,算法记作:f(n); 时间度量记作:T(n) = O( f(n) )。
它表示虽规模n的增大,算法 f(n) 执行时间的度量。
一般情况下,随着n的增大,T(n)增长最慢的算法为最优算法。
例如:逐个顺序查找,它的时间复杂度 O(n),是性能最差,而散列查找时间复杂度O(1) ,查找性能接近最优。
2. 空间复杂度
算法的空间复杂度,通过计算算法所需的存储空间,通常算法使用的存储空间,越少越好。
在某些特定业务场景,有“空间换时间”的策略,比如缓存,这里不再细述。
3. 全面评估
(1) 正确性:正确是最基本的要求。
(2) 可读性:便于阅读、理解、交流。
(3) 健壮性:当输入数据不合法时,也能做出相关处理,不会产生不需要的运行结果,甚至崩溃。
(4) 时间效率高、低存储空间
六、附(C语言知识点)
1. 结构体
1.1 理解
结构体,其实跟int , double 一样,它只是一种数据结构,它是由其他数据类型组合,构成的一种新数据类型。使其可以更直观、易于理解的方式,来表达客观事物。
1.2 定义
第一种形式: 有名称
struct Point
{
int x;
int y;
};
int main()
{
struct Point a = (struct Point){100, 200};
printf("a.x: %d, b.y:%d \n", a.x, a.y);
return 0;
}
提醒:定义结构体变量时,别漏了 struct, 错误的格式:Point a
第二种形式: 无名称
struct
{
int x;
int y;
} a, b;
int main()
{
a.x = 100;
a.y = 100;
printf("a.x: %d, b.y:%d \n", a.x, a.y);
return 0;
}说明: 只是定义了a, b 两个结构体变量,直接用就可以,结构体没有名称。无法再定义这个结构体的其他变量了。
第三种形式: 既有名称,也定义变量
struct Point
{
int x;
int y;
} a, b;
int main()
{
a.x = 100;
a.y = 100;
struct Point c = (struct Point) {1, 2};
printf("a.x: %d, b.y:%d \n", a.x, a.y);
return 0;
}2. typedef
typedef 就是给数据类型,起一个其他的别名。
例1:
typedef int my_int;
这时 my_int 与 int 就是等价的,可以按以下形式定义变量
my_int i = 100;
例2:
比较常见的是,给结构体,定义别名。
typedef struct node
{
int x;
int y;
} Point;
int main()
{
Point a = (Point) {1, 2};
printf("a.x: %d, b.y:%d \n", a.x, a.y);
return 0;
}补充说明: 此时直接 point a 就可以定义,当然也可以 struct node a 形式。只是别名形式更简洁。
3. 数组
3.1 定义
<类型> 数组名[数量]
int data[100];
C99之前,数量必须是整形常量,即在编译时刻,数组大小已确定。C99开始,可以是整形变量。
特点:
(1) 一旦创建不能改变大小。
(2) 期中所有元素,具有相同数据类型。
(3) 数组中的元素在内存中是连续排列的。
3.2 初始化
形式1:
int a[10] = {3, 4, 5, 6, 7}; // 数组长度10,按{}内的值初始化前5个,其余设置为0;
例如:
int a[10] = {}; //全部初始化为0。
int a[10] = {6}; //仅a[0]为6,其它都初始化为0。
int a[10] = {0}; // 同理,全部初始化为0。
形式2:
int a[] = {3, 4, 5, 6, 7}; // 数组长度为{}内数的个数,等价于:int a[5] = {3, 4, 5, 6, 7};
形式3:
int a[10] ; // 仅定义,没有初始化。
分情况:
(1) 全局数组变量,全部初始化为0。
(1) 静态数组变量时, 全部初始化为0。
(2) 局部数组变量,不会初始化,它的值是随机的。
#include <stdio.h>
int g_arr[10];
int main()
{
printf("\n\n全局变量 g_arr[10]的值: \n");
for(int i = 0; i < 10; i++) {
printf("%d ", g_arr[i]);
}
static int static_arr[10];
printf("\n\n静态变量 static_arr[10]的值: \n");
for(int i = 0; i < 10; i++) {
printf("%d ", static_arr[i]);
}
int arr[10];
printf("\n\n局部变量 arr[10]的值: \n");
for(int i = 0; i < 10; i++) {
printf("%d ", arr[i]);
}
printf("\nfinish!\n");
return 0;
}
执行结果:
全局变量 g_arr[10]的值:
0 0 0 0 0 0 0 0 0 0
静态变量 static_arr[10]的值:
0 0 0 0 0 0 0 0 0 0
局部变量 arr[10]的值:
0 0 0 0 8 0 4199705 0 8 0
finish!3.3 赋值
int a[5] = {1, 2, 6, 7, 9};
int b[5];
b = a; // 错误
可以用一下形式:
for(int i = 0; i < 5; i++)
{
b[i] = a[i];
}
或者采用memcpy函数形式, 需要引用 sring.h库。
#include <string.h>
memcpy(b, a, sizeof(a));
但作为函数的参数时,可以采用以下形式:
int max(int a[5], int size);
此时参数 int a[5] 中长度没有实际意义,这样写 int max(int a[], int size) 就可以了。
此时 max中int a[5],其实更像 int *a 形式,更确切,是C90后的 int *const a 形式。
4. 指针
4.1 形式
int main()
{
int a = 100;
int *p = &a;
// 因指针 *p 保存了 a 的地址,此时可以通过*p直接修改 a地址的数据。
*p = 200;
printf("a = %d \n", a);
return 0;
}运行结果: a = 200
4.2 注意
指针必须赋“地址”后,才可以对其指向的地址进行赋值操作。
以下是错误的逻辑:
int *p;
*p = 100;
因*p还没有指向一个有效的地址,此操作可能在一个莫名其妙的地址写值,会导致不可预测的结果。
5. 生存周期
全局变量、局部变量 (后续细化)
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








