斯坦福深度学习课程笔记（五）

训练神经网络

官网
ppt

激活函数

常见的激活函数有以下几种：

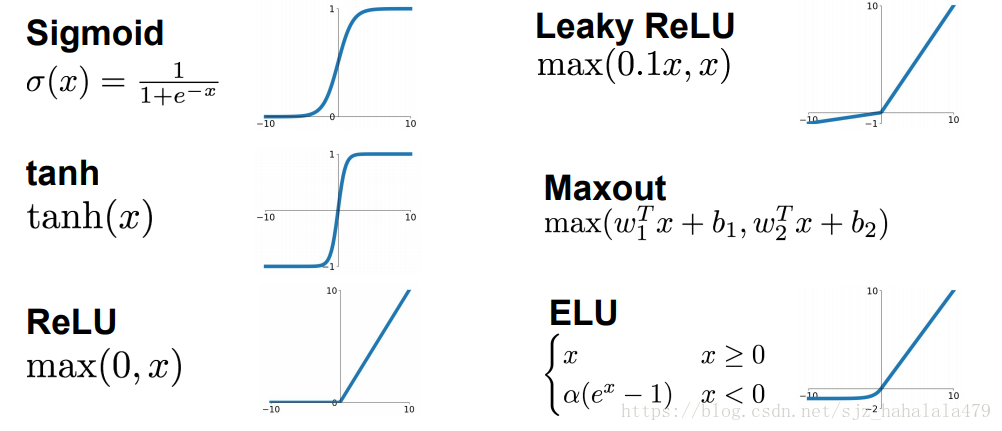
激活函数及对应导数

• sigmoid函数
  函数形式：$$f(x)=\frac{1}{1+e^{-x}}$$
  函数导数: $$f^{\prime }(x)=f(x)(1-f(x))$$
• tanh函数
  函数形式：$$f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$
  函数导数：$$f^{\prime }(x)=1-{(f(x))}^2$$
• relu函数：
  函数形式： $$f(x)=max(0,x)$$
  $$f^{\prime }(x)=\{\begin{array}{r}1,x>0\\ 0,x<=0\end{array}$$

1 sigmoid函数

这个函数的表达式一般为：
$$\theta (x)=\frac{1}{1+e^{-x}}$$
它会将所有输入的$x$值压缩到$(0,1)$区间中；
曾经这个函数是标准的激活函数，很多研究都用它，因为它对生物中神经元的“放电率”有一个很直观的模拟。

但是作为激活函数，它存在以下几个问题：

• 神经元饱和(saturated neurons)问题。我们发现，当输入值过大或过小时，sigmoid的梯度很容易接近0。在我们的认知中，梯度过于接近0并不好，它会使我们的迭代变得十分缓慢。
• sigmoid的输出不是zero-centered的。
  参考这两篇资料：
  谈谈激活函数中以零为中心的问题
  激活函数
  

对一个神经元而言，假设它的输入$x$都是正的，那么该神经元上权重$w$的梯度会是什么样呢？

由链式法则，$w$的梯度应该等于上游梯度times本地神经元的梯度。
$$\frac{\partial L}{\partial w}=\frac{\partial L}{\partial f}\cdot \frac{\partial f}{\partial w}$$
之前有计算过，$w$的本地梯度实际上就是输入$x$
$$\frac{\partial L}{\partial w}=\frac{\partial L}{\partial f}\cdot x$$
也就是说，在$\frac{\partial L}{\partial f}$确定的情况下，$w$梯度的符号由神经元的输入$x$决定。

如果此时神经元的输入总为positive值，那么神经元的$w$的梯度要不就都是正的，要不就都是负的。也就是说，$w_i$在更新值的时候，要不就是一起往变大的地方跑，要不就一起往变小的地方跑。如上图，假设$w$是二维的，$w$更新的方向，就是第一象限方向和第二象限方向。

但是如果最优解的$w$不是都往正或都往负呢？它可能是$w$的某些维度是往正的，某些维度是往负的，就像图中所示向第四象限伸展的$w$，这个$w$希望它的$w_x$维度增大，而$w_y$维度减小；sigmoid就无法满足完全沿着这个方向更新梯度，它只能像z字型一样，一会往右一会往下，这样扭曲地更新。这样迭代很明显要比直接沿着$w$的方向走要慢得多。

当然，以上的假设是基于我们输入的$x$符号都一致的情况。我们可以通过数据预处理使输入$x$符号不一致，这也是我们希望使用zero-mean data的原因之一。

• 第三个问题就是exp()操作比较computer expensive。这个问题其实并不大，因为之前的卷积操作实际上更computer expensive。

2 tanh函数

这个函数的表达式为
$$tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$

• tanh函数会将所有输入$x$压缩到$[-1,1]$。
• tanh函数的输出是zero-centered的，这是优于sigmoid的一点。
• 当输入较大或较小时，神经元依旧存在饱和问题。

3 ReLU函数

ReLU函数全称为Rectified Linear Unit，这个函数的表达式是
$$f(x)=max(0,x)$$

ReLU论文

• 可以注意到在正区域，这个函数避免了神经元饱和的现象。
• 非常computationally efficient
• 在实践中，我们发现它的收敛速度比sigmoid/tanh快很多（大概快6倍）。
• 在生物学的角度上，神经元的激活函数实际上更像ReLU，而非sigmoid

ReLU的问题在于

• 输出不是zero-center的
• 当输入$x\le 0$时，梯度全为0。
  

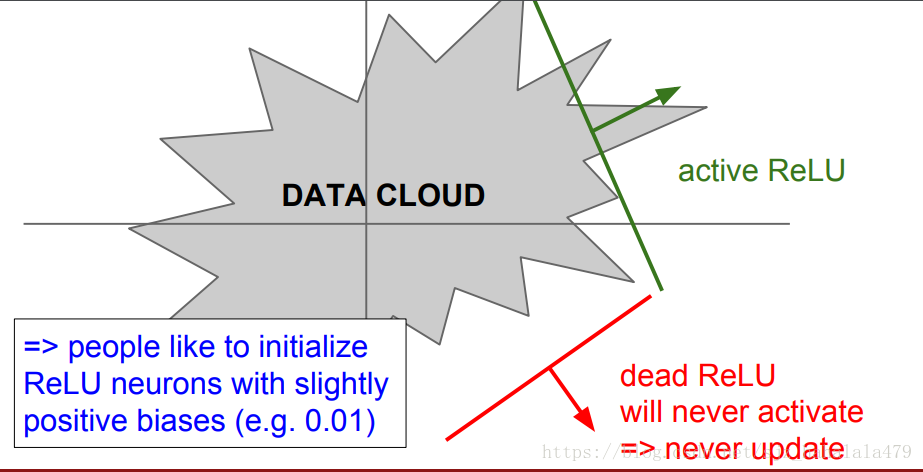
如果我们不能审慎地设计输入，使得输入全部$\le 0$的话，那么神经元不会被激活，$w$的梯度值也不会更新，这个ReLU就叫做Dead ReLU。

为了解决标准ReLU的问题，有几种ReLU的变体：

4 Leakly ReLU

这个函数的表达式为：
$$f(x)=(0.01x,x)$$
这样的表达解决了负区域内的神经元饱和问题；
不会出现dead ReLU的情况。

5 PReLU

前缀$P$的意思是Parametric参数的，函数表达式为
$$f(x)=(\alpha x,x)$$
刚刚的Leakly ReLU，其实就是$\alpha =0.01$的情况。
这里$\alpha$这个超参数，可以通过训练神经网络，学到比较好的$\alpha$。

5 Exponential ReLU (ELU)

这个函数也是ReLU的变体，

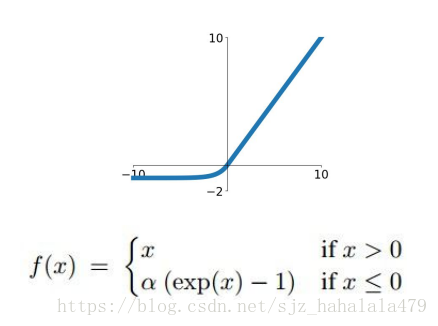
• 这个函数的输出接近于zero mean
• 和Leakly ReLU相比，ELU在负方向上也会存在神经元饱和的现象，有人说，这样的negative saturation regime可以增加对噪音的鲁棒性，在负方向上提供更健壮的反激活状态。

6 Maxout Neuron

Maxout神经元相当于ReLU和Leakly ReLU的泛化。
因为这个神经元就是求取输入$w_i{x}_i+b$的最大值。
当然这个神经元计算存在的问题就是会成倍地增加参数。

7 总结

• 主流上激活函数使用$ReLU$
• 要谨慎地设置学习率
• 可以尝试使用Leakly ReLU 、 ELU 、Maxout，但是它们的使用更多是实验上的，而非实践中
• 可以尝试使用tanh，但是不要期待它会优化很多
• 现在不用sigmoid了！

数据预处理

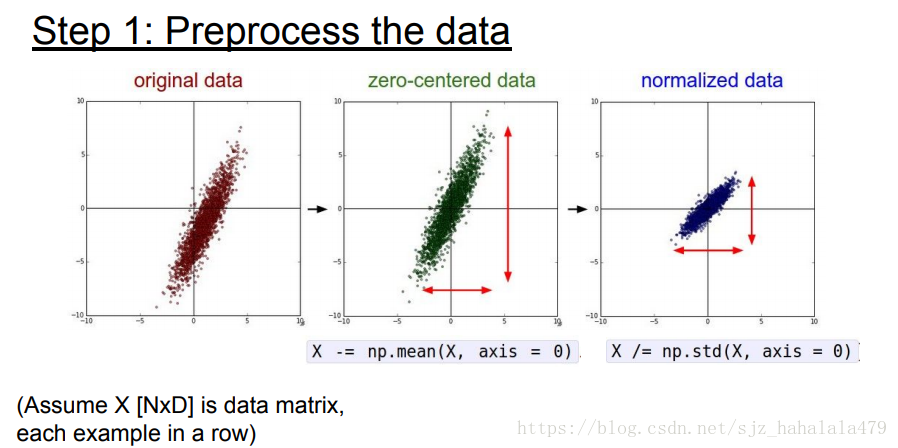
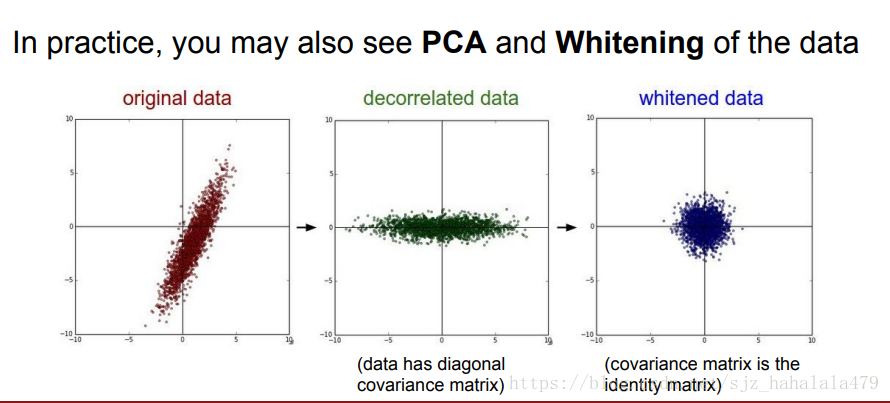
数据预处理，一般会使用mean方法使数据以0为中心；或者对数据做归一化；或者做PCA或者做whitening。但是对于图像数据，我们一般只做zero centered。

如图所示，有两种主流的做center的方法：

• 一种是将所有图像数据减去mean image。mean image是通过对所有训练的图像数据的每个像素点分别做均值得到的。
• 另一种方法是减去每个颜色通道的均值。

权重初始化

• 当我们的权重初始化为$0$时，会发生什么？
  最初的输入$wx+b$的结果就是$b$，对$b$再使用激活函数，然后再传给下一层神经元，…，再反向传播，我们最后会发现，所有的神经元都做同样的工作,更新同样的梯度，输出同样的值，这并不是我们想要的，我们想要的是不同的神经元能学到不同的东西。
• What if 我们给权重随机初始化一些较小的值？

W = np.random.randn(D,H) * 0.01

这里我们是给W按照标准正态分布随机初始化了一些值。
这样的初始化方法对小型网络是ok的，对深度网络就会出问题。

比如说以下这个例子，是10层，每层500个神经元的神经网络；$w$按照上述方式进行初始化。

import numpy as np

#assume some gaussian 10-D input data
D = np.random.randn(1000,500)
hidden_layer_size = [500]*10
nonlinearities = ['tanh']*len(hidden_layer_size)

act = {'relu':lambda x: np.maximum(0,x),'tanh':lambda x:np.tanh(x)}

Hs = {}
for i in range(len(hidden_layer_size)):
  X = D if i == 0 else Hs[i-1] #input at this layer
  fan_in = X.shape[1]
  fan_out = hidden_layer_size[i]
  W = np.random.randn(fan_in,fan_out) * 0.01 # layer initialization
  
  H = np.dot(X,W) #matrix multiply
  H = act[nonlinearities[i]](H)#nonlinearity
  Hs[i] = H #cache result on this layer

#look at distribution at each layer
print('input layer had maen %f and std %f' % (np.mean(D),np.std(D)))

layer_means = [np.mean(H) for i,H in Hs.items()]
layer_stds = [np.std(H) for i,H in Hs.items()]

for i,H in Hs.items():
  print('hidden layer %d had mean %f and std % f'%(i,layer_means[i],layer_stds[i]))

import matplotlib.pyplot as plt
plt.figure()
plt.subplot(121)
plt.plot(Hs.keys(),layer_means,'ob-')
plt.title('layer mean')
plt.subplot(122)
plt.plot(Hs.keys(),layer_stds,'or-')
plt.title('layer_std')

#plot the raw distributions
plt.figure()
for i,H in Hs.items():
  plt.subplot(1,len(Hs),i+1)
  plt.hist(H.ravel(),30,range(-1,1))

我们会发现没过几层，神经元的激活值都变为0了。第一层的数据分布还是一个比较合理的高斯分布值。过了一次迭代，数据值就都聚集在0附近了。

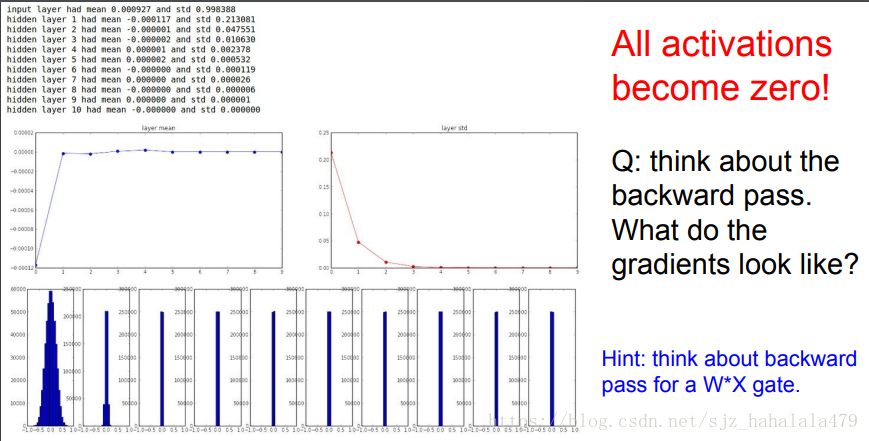
如果我们将权重值增大：

W = np.random.randn(D,H) * 1.0

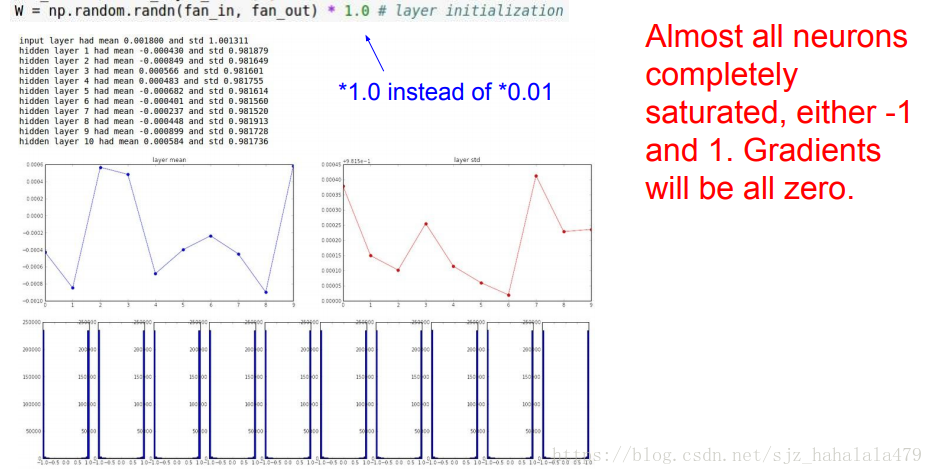
因为$\times 1.0$相当于一个比较大的权重，根据$tanh$的性质我们发现当输入较大或较小时，输出的梯度会趋向于0。在图中也会发现所有的神经元貌似都饱和了，值都在-1或+1处聚集。梯度都接近0。

Glorot 等人在2010年提出了Xavier初始化方法：

W = np.random.randn(D,H) / np.sqrt(fan_in)

这个方法通过使输入方差=输出方差，来使得最终神经元的值分布尽量拟合高斯曲线。

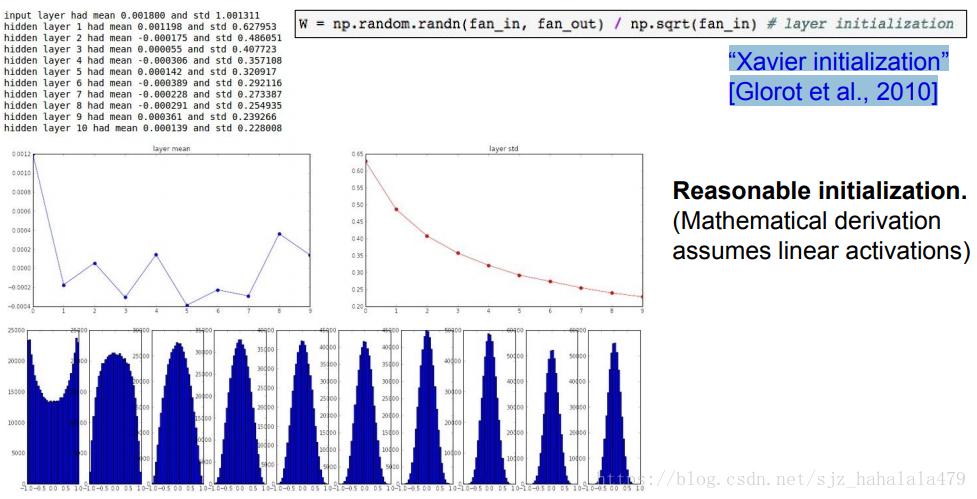
但是当激活函数是ReLU时，这个方法拟合的效果就不是很好。因为ReLU非中心对称的，且有一半的区域梯度为0。

这个时候可以使用

W = np.random.randn(D,H) / np.sqrt(2/fan_in)

来解决。（He et al., 2015）

现在如何合理地进行权重初始化依旧是活跃的研究领域。

批量归一化

翻译
a good spot 一个好的位置

参考文献
参考文献1
参考文献2

从之前的权值初始化部分我们可以看出，如果不好好调整超参数，神经元的激活值会很奇怪，以至于无法达到学习的目的。

所以，Ioffe and Szegedy等人在2015年提出了Batch Normalization(批量归一化)这个概念，通过手动地归一化神经元的输出值，来使该层的神经元分布符合高斯分布。调整的方法是：

• 计算该层所有输出值得经验均值
• 计算该层所有输出值得标准差
• 应用$${\hat{x}}^k=\frac{(x{)}^k-E[(x{)}^k]}{\sqrt{Var[(x{)}^k]}}$$求得新的神经元输出。（注意这里求得的是标准正态分布，以零为中心的）。

我们可以把一个Batch Normalization层看做下层神经元的预处理步骤，也可以将其看做上层神经元的后处理步骤。BN层一般在全连接层或者标准卷积层后插入，在非线性神经元之前插入。

但是标准正态分布有时候可能并不是最好的数据拟合分布，它可能存在一些拉伸或偏移。所以提出者加入了两个超参数 $\gamma$ 和 $\beta$，用来拟合有偏移的高斯分布。
$$y^{(k)}={\gamma }^{(k)}{\hat{x}}^{(k)}+{\beta }^{(k)}$$

Batch Normalization的具体算法如图左所示：

Batch Normalization的优势在于：

• 放松了我们对于初始化的依赖，我们可以使用更高的学习率
• 它有一点点像正则，也许用了它我们可以不用Dropout。

注意到，我们只在训练时更新BN层的均值和方差，在测试阶段，我们仍旧使用训练时的均值和方差。

监控学习过程

这一节主要是讲如何使整个神经网络的学习过程合理且可控。

1. 第一步是预处理数据
2. 第二步是选择架构
3. 然后训练时我们要检查loss是否合理
   首先我们将正则项设置为0，看看loss是不是符合我们定义好的规则；
   然后我们稍微增大loss，看看loss有没有相应地变大；
   接下来我们要调整学习率，我们调整好的学习率应该能使loss逐渐地变小；
   当我们发现loss收敛地很慢时，要适当增大学习率；
   当我们发现loss震荡甚至爆炸时，尤其是训练时我们发现NaN出现了，要减小学习率。

超参数优化

使用交叉验证的策略来进行超参数的优化

第一步：我们要在小数据上进行训练，只迭代几次，通过在小数据上训练来看看我们的网络有没有搭对（因为是小数据，所以当正则项为0时，loss也应该接近0），超参数合不合理。
第二步：我们要运行更长的时间，搜索更好地参数。

Random Search for Hyper-Parameter Optimization Bergstra and Bengio, 2012

搜索超参数的时候，使用Random Search比使用Grid Search。

优化算法

• SGD+Momentum 带动量的随机梯度下降
• Nesterov Momentum Nesterov动量
• AdaGrad Ada下降
• RMSProp
• Adam
• 正则化
• Dropout
• Data Augmentation 数据增益