刷leetcode动态规划类题目总结

最新推荐文章于 2025-03-12 11:57:51 发布

原创最新推荐文章于 2025-03-12 11:57:51 发布 · 106 阅读

CC 4.0 BY-SA版权

本文深入探讨了动态规划的基本思路和步骤，将其概括为模型公式建立、初始化和状态更新三部分。通过举例展示了如何应用动态规划解决找到二维网格中从原点到目标点的最短路径问题。在示例中，动态规划矩阵dp[i][j]表示到达点[i][j]的路径条数，并通过迭代更新得到最终答案。动态规划是一种有效的解决最优化问题的算法，适用于多种计算机科学领域的挑战。

动态规划基本思路：假设dp[i]=a，解释a为第i个或者前i个满足条件的值。那么dp[i]和dpj有很大的联系。也就是说“咋不知道，咋不愿意问，咋只知道前面所有数值中满足条件的那个”。
按照这个思路，动态规划算法总结起来可以分为以下三步：
（1）建立模型公式（确定dp数组的格式，注意是维度和dp矩阵中的初始值到底是0还是一个无穷大的数）
（2）对dp数组进行初始化，这一步非常重要，要首先知道dp元组中数值的含义。
（3）根据模型公式，更新dp[i][j]，得到最终的答案
为了更好的解释动态规划算法，以一道例题为例
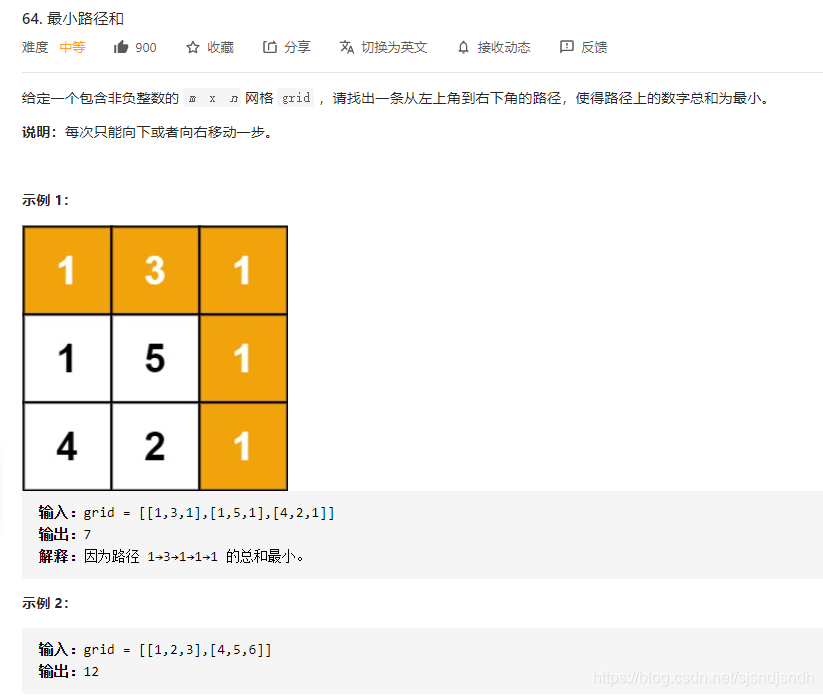
在这里插入图片描述
根据动态规划三部曲套路：
（1）首先定义模型公式。假设dp[i][j]为原点到点[i][j]的路径条数。
（2））由于只能向左和向右移动，因此到dp[i][j]=dp[i-1][j]+dp[i][j-1]。随后初始化dp，dp[0][0]=0,dp[i][0]=1,dp[0][j]=0。
（3）根据模型公式，最终求出dp[m-1][n-1]的值。

class Solution:
    def minPathSum(self, grid: List[List[int]]) -> int:
        rows, colums=len(grid),len(grid[0])
        dp=[[0]*colums for _ in range(rows)]
        dp[0][0]=grid[0][0]
        for i in range(1,rows):
            dp[i][0]=dp[i-1][0]+grid[i][0]
        for j in range(1,colums):
            dp[0][j]=dp[0][j-1]+grid[0][j]
        for i in range(1,rows):
            for j in range(1,colums):
                dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i][j]
        return dp[rows-1][colums-1]