[Java]二叉树-优快云博客

本文链接：https://blog.youkuaiyun.com/sjhdaj/article/details/130027094

文章介绍了树的基本性质，包括度、节点数的计算以及树的两种存储结构——孩子双亲表示法和孩子表示法。接着详细讲解了二叉树的分类，如普通、满、完全、二叉排序和平衡二叉树，并阐述了四种遍历方法：先序、中序、后序和层序遍历。此外，还提到了二叉树的一些基本操作，如获取节点数、叶子节点数、指定层数节点数和判断是否为完全二叉树的方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、树的认识

树是一种递归的非线性结构，是一种由n个结点组成的具有层次关系的集合。

树的度是指各节点度的最大值，度指一个结点上有几个分支。

m叉树——每个节点最多只能有m个孩子的树

1. 树的基本性质

1、树中的结点数等于所有结点的度数之和+1

2、度为m的树中第i层上至多有m^(i-1)个结点【树是从第一层开始往下数的】

3、高度为h的m叉树嘴多有（m^h-1/m -1）个结点

4、高度为h，度为m的树至少有h+m-1个结点

2. 树的存储结构

1. 孩子双亲表示法

class Node{
    int val;
    Node left;
    Node right;
    Node parent;
}

2. 孩子表示法

class Node{
    int val;
    Node left;
    Node right;
}

二、二叉树

二叉树与度为2的树的区别：

1.二叉树可以为空，度为2的有序树最起码有三个结点

2. 有序树的次序是孩子结点相对于另一个孩子结点而言的，如果只有一个孩子结点，则不分左右次序，而二叉树无论孩子数是否为2，都需要确定左右次序

1. 二叉树的分类

1. 普通二叉树

2. 满二叉树：每一层含有最多的结点，i层一共含有（2^i）-1个结点，一个结点编号i，它的左子树是2i，右子树是2i+1，双亲为i/2向下取整。

3. 完全二叉树：非满二叉树（把满二叉树中编号较大的结点去掉），最多只有一个结点的度为1，而且该结点的孩子仅仅是左子树。

4. 二叉排序树：根节点关键字大于所有左子树的关键字，小于所有右子树的关键字。

5. 平衡二叉树：树上任意结点的左右子树深度之差不超过1，特殊的二叉排序树。

2. 二叉树的遍历

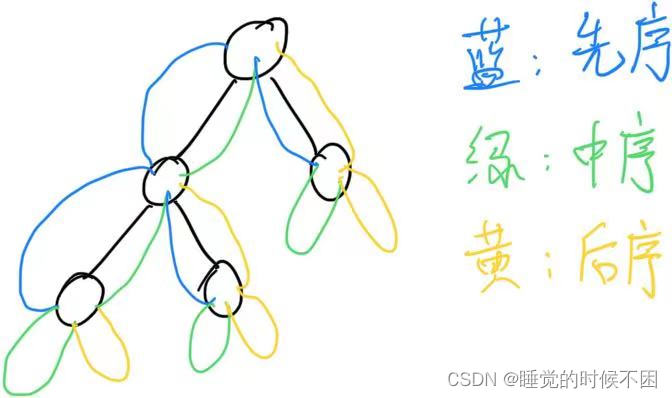
1. 先序遍历

访问根节点=》先序遍历左子树=》先序遍历右子树

//递归遍历
void preOrder(TreeNode root){
        if(root == null){
            return;
        }
        System.out.println(root.val+" ");
        preOrder(root.left);
        preOrder(root.right);
    }

//非递归遍历
public void preOrderNor(TreeNode root){
        if(root == null){
            return;
        }
        TreeNode cur = root;
        Deque<TreeNode> stack = new ArrayDeque<>();
        while(cur != null || !stack.isEmpty()){
            while(cur != null){
                stack.push(cur);
                System.out.print(cur.val+" ");
                cur = cur.left;
            }
            TreeNode top = stack.pop();
            cur = top.right;
        }
    }

2. 中序遍历

中序遍历左子树=》访问根节点=》中序遍历右子树

//递归遍历
void inOrder(TreeNode root){
        if(root == null){
            return;
        }
        preOrder(root.left);
        System.out.println(root.val+" ");
        preOrder(root.right);
    }

//非递归遍历
public void inOrderNor(TreeNode root) {
        if (root == null) {
            return;
        }
        TreeNode cur = root;
        Deque<TreeNode> stack = new ArrayDeque<>();
        while (cur != null || !stack.isEmpty()) {
            while (cur != null) {
                stack.push(cur);
                cur = cur.left;
            }
            TreeNode top = stack.pop();
            System.out.print(top.val + " ");
            cur = top.right;
        }
    }

3. 后序遍历

后序遍历左子树=》后序遍历右子树=》访问根节点

//递归遍历
void postOrder(TreeNode root){
        if(root == null){
            return;
        }
        preOrder(root.left);
        preOrder(root.right);
        System.out.println(root.val+" ");
    }

//非递归遍历
public void postOrderNor(TreeNode root){
        if (root == null) {
            return;
        }
        TreeNode cur = root;
        TreeNode prev = null;
        Deque<TreeNode> stack = new ArrayDeque<>();
        while (cur != null || !stack.isEmpty()) {
            while (cur != null) {
                stack.push(cur);
                cur = cur.left;
            }
            TreeNode top = stack.peek();
            if(cur.right == null || prev == top.right){
                System.out.print(top.val+" ");
                stack.pop();
                prev = top;
            }else {
                cur = top.right;
            }
        }
    }