基本排序算法

最新推荐文章于 2023-10-01 17:03:58 发布

rugu-sco

最新推荐文章于 2023-10-01 17:03:58 发布

阅读量246

点赞数

CC 4.0 BY-SA版权

分类专栏： C 数据结构与算法文章标签：排序

本文链接：https://blog.youkuaiyun.com/sinat_36629696/article/details/80501982

C 同时被 2 个专栏收录

29 篇文章

订阅专栏

数据结构与算法

20 篇文章

订阅专栏

冒泡排序

基本步骤:

从第一个元素开始, 依次比较相邻两个元素的大小, 如果前面的大于后面的, 就交换, 交换完, 此时, 最后一个元素就是最大的.
然后除了最后一个元素, 其余元素再重复以上步骤
直到需要比较的元素越来越少, 只剩最后一个, 此时就有序了.

///////////////////////////////////////////////
// 1, 冒泡排序
//    时间复杂度: O(n^2)
//    空间复杂度: O(1)
//    稳定的
//////////////////////////////////////////////
void BubbleSort(int arr[], size_t size)
{
    if(size <= 1)
    {
        return ;
    }
    int bound = 0;
    int cur = 0;
    for(; bound < size; ++bound)
    {
        cur = size - 1;
        for(; cur > bound; --cur)
        {
            if(arr[cur] < arr[cur - 1])
            {
                Swap(&arr[cur], &arr[cur - 1]);
            }
        } // 第二重循环
    } // 第一重循环
}

选择排序

每一次从待排序数组中选择出最小(最大)的值放到序列起始位置, 直到所有元素排完.
这里写图片描述

/////////////////////////////////////////////
// 2, 选择排序
//    时间复杂度: O(n^2)
//    空间复杂度: O(1)
//    不稳定
/////////////////////////////////////////////
void SelectSort(int arr[], size_t size)
{
    if(size <= 1)
      return ;
    size_t bound = 0;
    for(; bound<size; ++bound)
    {
        size_t cur = bound + 1;
        for(; cur < size; ++cur)
        {
            if(arr[cur] < arr[bound])
            {
                Swap(&arr[cur], &arr[bound]);
            }
        } // 第二重循环
    } // 第一重循环
}

插入排序

把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中，直到所有的记录插入完为止，得到一个新的有序序列.

///////////////////////////////////////////
// 3, 插入排序
//    时间复杂度:O(n^2)
//    空间复杂度:O(1)
//    稳定的
///////////////////////////////////////////
void InsertSort(int arr[], size_t size)
{
    if(size <= 1)
      return ;
    size_t bound = 1;
    for(; bound < size; ++bound)
    {
        // 保存arr[bound] 是为了后面的还原
        int bound_value = arr[bound];
        size_t cur = bound;
        for(; cur > 0; --cur)
        {
            if(arr[cur-1] > bound_value)
            {
                arr[cur] = arr[cur-1];
            }
            else
            {
                break;
            }
        }
        arr[cur] = bound_value;
    }
}

堆排序

基本步骤:

根据数组建立一个堆, 升序建立大堆, 降序建立小堆
每次将堆顶元素与最后一个元素交换, 堆的大小减 1
交换完, 要经过调整, 保证剩余的元素依然是一个堆
直到堆的大小为 1, 此时就有序了.

//////////////////////////////////////////////
// 4, 堆排序
//    时间复杂度: O(N*logN)
//    空间复杂度: O(1)
//    不稳定
/////////////////////////////////////////////
// 升序: 建立大堆
// 降序: 建立小堆
// 步骤: 1, 先根据数组建立一个堆
//       2, 依次交换堆顶元素和最后一个元素, 并删除最后一个元素
//       3, 堆为空时, 数组就有序了
// 建堆方法:
//       1, 下沉式调整:
//          a) 从后往前遍历数组, 找到第一个非叶子节点
//          b) 再找到它的父节点
//          c) 和它父节点比较, 是否需要交换
void AdjustDown(int arr[], size_t size, size_t i)
{
    if(size <= 1)
      return ;
    size_t parent = i;
    // 找到它的左孩子节点
    size_t child = 2 * parent + 1;
    while(child < size)
    {
        // 先比较左右孩子节点的大小, 找到较大的
        if(child + 1 < size && arr[child] < arr[child+1])
        {
            child = child+1;
        }
        // 再和父节点比较, 因为要建立大堆, 所以大于父节点就交换
        if(arr[child] > arr[parent])
        {
            Swap(&arr[child], &arr[parent]);
        }
        // 更新父节点, 孩子节点
        parent = child;
        child = 2 * parent + 1;
    }
}
void AdjustUp(int arr[], size_t bound)
{
    size_t child = bound;
    size_t parent = (child - 1) / 2;
    while(child > 0)
    {
        if(arr[parent] < arr[child])
        {
            Swap(&arr[parent], &arr[child]);
        }
        else
        {
            break;
        }
        child = parent;
        parent = (child - 1) / 2;
    }
}
void HeapCreate(int arr[], size_t size)
{
    if(size <= 1)
    {
        return ;
    }
#if 0
    // 1, 下沉式调整
    // 从最后一个非叶子节点开始
    size_t i = (size-1-1)/2;
    for(; i>0; --i)
    {
        AdjustDown(arr, size, i);
    }
    AdjustDown(arr, size, i);
#else
    // 2, 上浮式调整
    size_t bound = 0;
    for(; bound < size; ++bound)
    {
        AdjustUp(arr, bound + 1);
    }
#endif
}
void HeapPop(int arr[], size_t heap_size)
{
    // 当堆只剩下一个元素时, 就已经有序了
    if(heap_size <= 1)
      return ;
    // 将堆顶元素和当前堆的最后一个元素交换
    Swap(&arr[0], &arr[heap_size - 1]);
    AdjustDown(arr, heap_size-1, 0);
}
void HeapSort(int arr[], size_t size)
{
    if(size <= 1)
    {
        return ;
    }
    // 先基于数组根据升序还是降序, 建立一个大堆或小堆
    HeapCreate(arr, size);
    size_t i = 0;
    for(; i < size; i++)
    {
        // 依次交换堆顶元素和最后一个元素
        // 然后"删除"最后一个元素, 重新调整堆
        // 使其重新满足堆的规则
        HeapPop(arr, size-i); // size - i 表示当前堆的大小
    }
}

希尔排序

插入排序的改进版本
设置一个步长 gap , 根据 gap 分组, 然后对每组分别进行插入排序
因为插入排序的特点为: 1, 元素越少效率越高 2, 序列越有序效率越高
步长的设置规则为 gap = N / 2 , N / 4 , N / 8 , … 1

//////////////////////////////////////////////////
// 5, 希尔排序
//    时间复杂度: O(N ^ 2), 如果gap选择适当, 可以达到O(N ^ 1.3)
//    空间复杂度: O(1)
//    不稳定的
//////////////////////////////////////////////////
// 插入排序的改进版本
// 设置步长 gap
// 根据 gap 分组, 然后对每组分别进行插入排序
// 步长设置采用希尔序列: gap = N/2 N/4 N/8 ... 1
void ShellSort(int arr[], size_t size)
{
    if(size <= 1)
      return ;
    size_t gap = size / 2; //初始步长
    for(; gap > 0; gap /= 2) //步长每次 / 2
    {
        size_t bound = gap;
        for(; bound < size; ++bound)
        {
            int bound_value = arr[bound];
            size_t cur = bound;
            for(; cur >= gap; cur -= gap) //cur -= gap 找到它同组的前一个元素
            {
                if(arr[cur - gap] > bound_value)
                {
                    Swap(&arr[cur], &arr[cur - gap]);
                }
                else
                {
                    break;
                }
            }
            //arr[cur] = bound_value;
        } // 第二重循环
    } // 第一重循环
}

归并排序

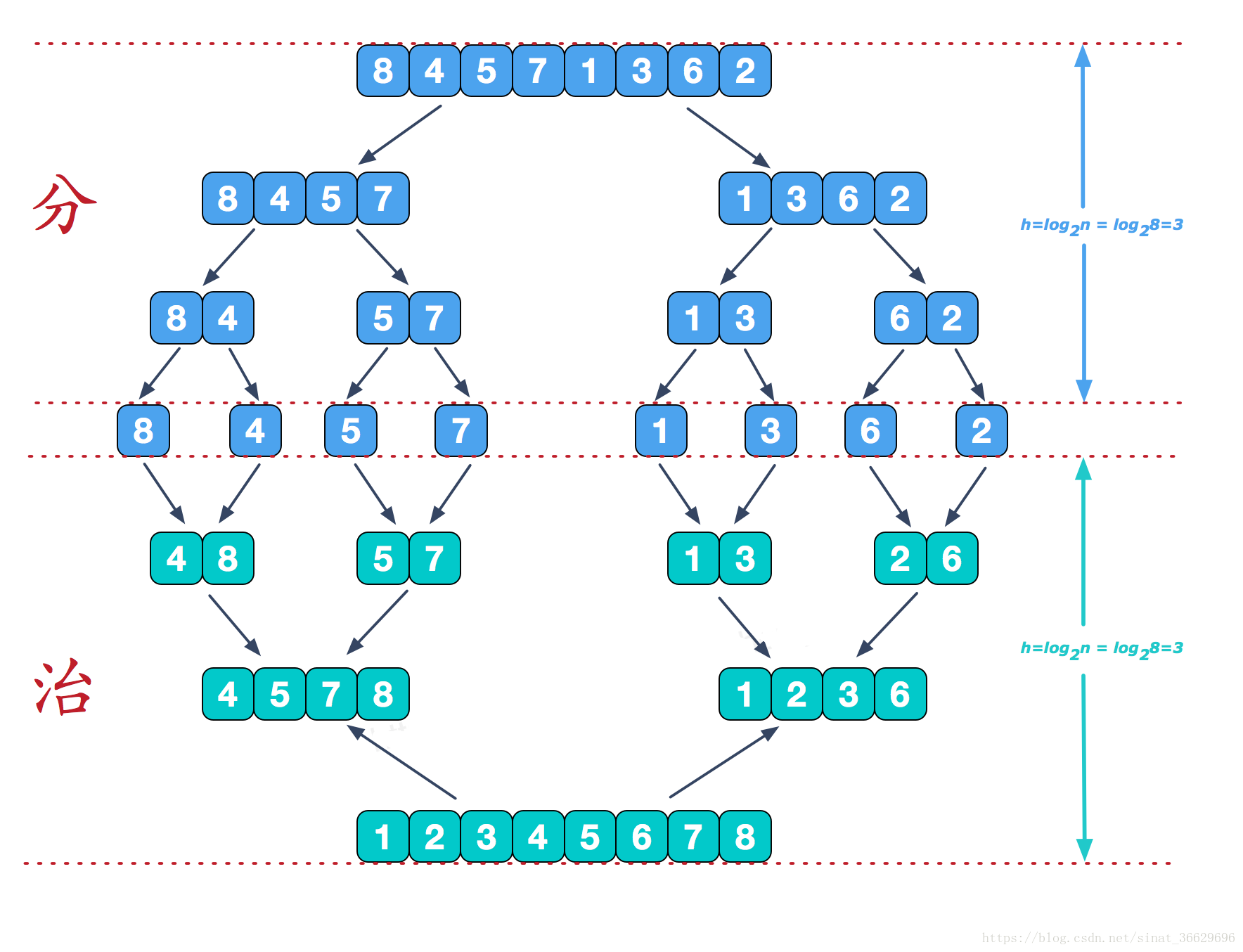
这里写图片描述
类比将两个有序的单链表合并为一个有序的单链表
设置两个指针分别指向两个链表, 然后比较所对应的值的大小, 将较小的放入有序序列中, 然后指针后移, 继续比较.

////////////////////////////////////////////
// 6, 归并排序
//    时间复杂度: O(N*logN)
//    空间复杂度: O(N)
//    稳定的
////////////////////////////////////////////
// 递归版本
void _MergeArray(int arr[], int64_t beg, int64_t mid, int64_t end, int* tmp)
{
    // 两个数组的首元素下标
    int64_t arr1_beg = beg;
    int64_t arr2_beg = mid;
    // tmp数组的下标
    int64_t tmp_index = beg;
    while(arr1_beg < mid && arr2_beg < end)
    {
        // 比较两个数组的首元素, 较小的放入tmp数组
        if(arr[arr1_beg] < arr[arr2_beg])
        {
            tmp[tmp_index++] = arr[arr1_beg++];
        }
        else
        {
            tmp[tmp_index++] = arr[arr2_beg++];
        }
    }
    // 循环结束, 将剩下的数组元素接到tmp后面
    while(arr1_beg < mid)
    {
        tmp[tmp_index++] = arr[arr1_beg++];
    }
    while(arr2_beg < end)
    {
        tmp[tmp_index++] = arr[arr2_beg++];
    }
    // 最后再将tmp的元素拷贝到arr数组
    memcpy(arr+beg, tmp+beg, sizeof(int)*(end - beg));
}
void _MergeSort(int arr[], int64_t beg, int64_t end, int* tmp)
{
    if(end - beg <= 1)
      return ;
    if(beg < end)
    {
        int64_t mid = beg + (end - beg) / 2;
        // 此时有了两个区间 [beg, mid), [mid, end)
        // 将这两个区间分别再递归排序
        _MergeSort(arr, beg, mid, tmp);
        _MergeSort(arr, mid, end, tmp);
        _MergeArray(arr, beg, mid, end, tmp);
    }
}
void MergeSort(int arr[], int64_t size)
{
    if(size <= 1)
      return ;
    // 申请临时空间tmp进行归并
    int* tmp = (int*)malloc(sizeof(int)*size);
    int beg = 0;
    _MergeSort(arr, beg, size, tmp);
    free(tmp);
}
// 非递归版本归并排序
void MergeSortByLoop(int arr[], size_t size)
{
    if(size <= 1)
      return ;
    int* tmp = (int*)malloc(sizeof(int)*size);
    // 设置步长 gap = 1, 2, 4 ...
    size_t gap = 1;

    for(; gap < size; gap *= 2)
    {
        size_t i = 0;
        for(; i < size; i += 2*gap)
        {
            size_t beg = i;
            size_t mid = i + gap;
            size_t end = i + 2*gap;
            if(mid > size)
              mid = size;
            if(end > size)
              end = size;
            _MergeArray(arr, beg, mid, end, tmp);
        }
    } // 第一重循环
}

快速排序

冒泡排序的改进版本
快速排序之所比较快，因为相比冒泡排序，每次交换是跳跃式的。
每次排序的时候设置一个基准点
将小于等于基准点的数全部放到基准点的左边
将大于等于基准点的数全部放到基准点的右边
这样在每次交换的时候就不会像冒泡排序一样每次只能在相邻的数之间进行交换，交换的距离就大的多了。
因此总的比较和交换次数就少了，速度自然就提高了。当然在最坏的情况下，仍可能是相邻的两个数进行了交换。因此快速排序的最差时间复杂度和冒泡排序是一样的都是O(N^2)，它的平均时间复杂度为O(N*logN)

////////////////////////////////////////////////
// 快速排序
// 时间复杂度: O(N * logN), 最坏情况:O(N^2)
// 空间复杂度: O(N)
// 不稳定
////////////////////////////////////////////////
// 交换法
int64_t partion_swap(int arr[], int64_t beg, int64_t end)
{
    if(end - beg <= 1)
      return beg;
    int64_t left = beg;
    int64_t right = end - 1;
    int key = arr[end - 1]; // 最后一个元素为基准值
    while(left < right)
    {
        // 从左往右找一个比 key 大的数
        while(left < right && arr[left] <= key)
          ++left;
        // 从右往左找一个比 key 小的数
        while(left < right && arr[right] >= key)
          --right;
        if(left < right)
          Swap(&arr[left], &arr[right]);
    }
    // 最后将 left 指向的位置和 key 交换
    Swap(&arr[left], &arr[end - 1]);
    return left;
}
// 挖坑法
int64_t partion_Trenching(int arr[], int64_t beg, int64_t end)
{
    if(end - beg <= 1)
      return beg;
    int64_t left = beg;
    int64_t right = end - 1;
    int key = arr[end - 1];
    while(left < right)
    {
        // 从左往右找一个比 key 大的数
        while(left < right && arr[left] <= key)
          ++left;
        if(left < right)
          arr[right--] = arr[left];
        // 从右往左找一个比 key 小的数
        while(left < right && arr[right] >= key)
          --right;
        if(left < right)
          arr[left++] = arr[right];
    }
    // 退出循环,还剩最后一个坑
    arr[left] = key;
    return left;
}
void _QuickSort(int arr[], int64_t beg, int64_t end)
{
    if(end - beg <= 1)
      return ;
    //int64_t mid = partion_swap(arr, beg, end);
    int64_t mid = partion_Trenching(arr, beg, end);
    _QuickSort(arr, beg, mid);
    _QuickSort(arr, mid+1, end);
}
void QuickSort(int arr[], size_t size)
{
    if(size <= 1)
      return ;
    int64_t beg = 0;
    int64_t end = size;
    _QuickSort(arr, beg, end);
}

源代码

/*================================================================

# File Name: Sort.c
# Author: rjm
# mail: rjm96@foxmail.com
# Created Time: 2018年05月25日 星期五 20时16分47秒

================================================================*/

#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>
#include <string.h>

#define TEST_HEAD printf("\n============%s================\n", __FUNCTION__)

void Swap(int* a, int* b)
{
    int tmp = *a;
    *a = *b;
    *b = tmp;
}
///////////////////////////////////////////////
// 1, 冒泡排序
//    时间复杂度: O(n^2)
//    空间复杂度: O(1)
//    稳定的
//////////////////////////////////////////////
void BubbleSort(int arr[], size_t size)
{
    if(size <= 1)
    {
        return ;
    }
    int bound = 0;
    int cur = 0;
    for(; bound < size; ++bound)
    {
        cur = size - 1;
        for(; cur > bound; --cur)
        {
            if(arr[cur] < arr[cur - 1])
            {
                Swap(&arr[cur], &arr[cur - 1]);
            }
        } // 第二重循环
    } // 第一重循环
}

/////////////////////////////////////////////
// 2, 选择排序
//    时间复杂度: O(n^2)
//    空间复杂度: O(1)
//    不稳定
/////////////////////////////////////////////
void SelectSort(int arr[], size_t size)
{
    if(size <= 1)
      return ;
    size_t bound = 0;
    for(; bound<size; ++bound)
    {
        size_t cur = bound + 1;
        for(; cur < size; ++cur)
        {
            if(arr[cur] < arr[bound])
            {
                Swap(&arr[cur], &arr[bound]);
            }
        } // 第二重循环
    } // 第一重循环
}

///////////////////////////////////////////
// 3, 插入排序
//    时间复杂度:O(n^2)
//    空间复杂度:O(1)
//    稳定的
///////////////////////////////////////////
void InsertSort(int arr[], size_t size)
{
    if(size <= 1)
      return ;
    size_t bound = 1;
    for(; bound < size; ++bound)
    {
        // 保存arr[bound] 是为了后面的还原
        int bound_value = arr[bound];
        size_t cur = bound;
        for(; cur > 0; --cur)
        {
            if(arr[cur-1] > bound_value)
            {
                arr[cur] = arr[cur-1];
            }
            else
            {
                break;
            }
        }
        arr[cur] = bound_value;
    }
}
//////////////////////////////////////////////
// 4, 堆排序
//    时间复杂度: O(N*logN)
//    空间复杂度: O(1)
//    不稳定
/////////////////////////////////////////////
// 升序: 建立大堆
// 降序: 建立小堆
// 步骤: 1, 先根据数组建立一个堆
//       2, 依次交换堆顶元素和最后一个元素, 并删除最后一个元素
//       3, 堆为空时, 数组就有序了
// 建堆方法:
//       1, 下沉式调整:
//          a) 从后往前遍历数组, 找到第一个非叶子节点
//          b) 再找到它的父节点
//          c) 和它父节点比较, 是否需要交换
void AdjustDown(int arr[], size_t size, size_t i)
{
    if(size <= 1)
      return ;
    size_t parent = i;
    // 找到它的左孩子节点
    size_t child = 2 * parent + 1;
    while(child < size)
    {
        // 先比较左右孩子节点的大小, 找到较大的
        if(child + 1 < size && arr[child] < arr[child+1])
        {
            child = child+1;
        }
        // 再和父节点比较, 因为要建立大堆, 所以大于父节点就交换
        if(arr[child] > arr[parent])
        {
            Swap(&arr[child], &arr[parent]);
        }
        // 更新父节点, 孩子节点
        parent = child;
        child = 2 * parent + 1;
    }
}
void AdjustUp(int arr[], size_t bound)
{
    size_t child = bound;
    size_t parent = (child - 1) / 2;
    while(child > 0)
    {
        if(arr[parent] < arr[child])
        {
            Swap(&arr[parent], &arr[child]);
        }
        else
        {
            break;
        }
        child = parent;
        parent = (child - 1) / 2;
    }
}
void HeapCreate(int arr[], size_t size)
{
    if(size <= 1)
    {
        return ;
    }
#if 0
    // 1, 下沉式调整
    // 从最后一个非叶子节点开始
    size_t i = (size-1-1)/2;
    for(; i>0; --i)
    {
        AdjustDown(arr, size, i);
    }
    AdjustDown(arr, size, i);
#else
    // 2, 上浮式调整
    size_t bound = 0;
    for(; bound < size; ++bound)
    {
        AdjustUp(arr, bound + 1);
    }
#endif
}
void HeapPop(int arr[], size_t heap_size)
{
    // 当堆只剩下一个元素时, 就已经有序了
    if(heap_size <= 1)
      return ;
    // 将堆顶元素和当前堆的最后一个元素交换
    Swap(&arr[0], &arr[heap_size - 1]);
    AdjustDown(arr, heap_size-1, 0);
}
void HeapSort(int arr[], size_t size)
{
    if(size <= 1)
    {
        return ;
    }
    // 先基于数组根据升序还是降序, 建立一个大堆或小堆
    HeapCreate(arr, size);
    size_t i = 0;
    for(; i < size; i++)
    {
        // 依次交换堆顶元素和最后一个元素
        // 然后"删除"最后一个元素, 重新调整堆
        // 使其重新满足堆的规则
        HeapPop(arr, size-i); // size - i 表示当前堆的大小
    }
}

//////////////////////////////////////////////////
// 5, 希尔排序
//    时间复杂度: O(N ^ 2), 如果gap选择适当, 可以达到O(N ^ 1.3)
//    空间复杂度: O(1)
//    不稳定的
//////////////////////////////////////////////////
// 插入排序的改进版本
// 设置步长 gap
// 根据 gap 分组, 然后对每组分别进行插入排序
// 步长设置采用希尔序列: gap = N/2 N/4 N/8 ... 1
void ShellSort(int arr[], size_t size)
{
    if(size <= 1)
      return ;
    size_t gap = size / 2; //初始步长
    for(; gap > 0; gap /= 2) //步长每次 / 2
    {
        size_t bound = gap;
        for(; bound < size; ++bound)
        {
            int bound_value = arr[bound];
            size_t cur = bound;
            for(; cur >= gap; cur -= gap) //cur -= gap 找到它的前一个元素
            {
                if(arr[cur - gap] > bound_value)
                {
                    Swap(&arr[cur], &arr[cur - gap]);
                }
                else
                {
                    break;
                }
            }
            //arr[cur] = bound_value;
        } // 第二重循环
    } // 第一重循环
}

////////////////////////////////////////////
// 6, 归并排序
//    时间复杂度: O(N*logN)
//    空间复杂度: O(N)
//    稳定的
////////////////////////////////////////////
// 递归版本
void _MergeArray(int arr[], int64_t beg, int64_t mid, int64_t end, int* tmp)
{
    // 两个数组的首元素下标
    int64_t arr1_beg = beg;
    int64_t arr2_beg = mid;
    // tmp数组的下标
    int64_t tmp_index = beg;
    while(arr1_beg < mid && arr2_beg < end)
    {
        // 比较两个数组的首元素, 较小的放入tmp数组
        if(arr[arr1_beg] < arr[arr2_beg])
        {
            tmp[tmp_index++] = arr[arr1_beg++];
        }
        else
        {
            tmp[tmp_index++] = arr[arr2_beg++];
        }
    }
    // 循环结束, 将剩下的数组元素接到tmp后面
    while(arr1_beg < mid)
    {
        tmp[tmp_index++] = arr[arr1_beg++];
    }
    while(arr2_beg < end)
    {
        tmp[tmp_index++] = arr[arr2_beg++];
    }
    // 最后再将tmp的元素拷贝到arr数组
    memcpy(arr+beg, tmp+beg, sizeof(int)*(end - beg));
}
void _MergeSort(int arr[], int64_t beg, int64_t end, int* tmp)
{
    if(end - beg <= 1)
      return ;
    if(beg < end)
    {
        int64_t mid = beg + (end - beg) / 2;
        // 此时有了两个区间 [beg, mid), [mid, end)
        // 将这两个区间分别再递归排序
        _MergeSort(arr, beg, mid, tmp);
        _MergeSort(arr, mid, end, tmp);
        _MergeArray(arr, beg, mid, end, tmp);
    }
}
void MergeSort(int arr[], int64_t size)
{
    if(size <= 1)
      return ;
    // 申请临时空间tmp进行归并
    int* tmp = (int*)malloc(sizeof(int)*size);
    int beg = 0;
    _MergeSort(arr, beg, size, tmp);
    free(tmp);
}
// 非递归版本归并排序
void MergeSortByLoop(int arr[], size_t size)
{
    if(size <= 1)
      return ;
    int* tmp = (int*)malloc(sizeof(int)*size);
    // 设置步长 gap = 1, 2, 4 ...
    size_t gap = 1;

    for(; gap < size; gap *= 2)
    {
        size_t i = 0;
        for(; i < size; i += 2*gap)
        {
            size_t beg = i;
            size_t mid = i + gap;
            size_t end = i + 2*gap;
            if(mid > size)
              mid = size;
            if(end > size)
              end = size;
            _MergeArray(arr, beg, mid, end, tmp);
        }
    } // 第一重循环
}
////////////////////////////////////////////////
// 快速排序
// 时间复杂度: O(N * logN), 最坏情况:O(N^2)
// 空间复杂度: O(N)
// 不稳定
////////////////////////////////////////////////
// 交换法
int64_t partion_swap(int arr[], int64_t beg, int64_t end)
{
    if(end - beg <= 1)
      return beg;
    int64_t left = beg;
    int64_t right = end - 1;
    int key = arr[end - 1]; // 最后一个元素为基准值
    while(left < right)
    {
        // 从左往右找一个比 key 大的数
        while(left < right && arr[left] <= key)
          ++left;
        // 从右往左找一个比 key 小的数
        while(left < right && arr[right] >= key)
          --right;
        if(left < right)
          Swap(&arr[left], &arr[right]);
    }
    // 最后将 left 指向的位置和 key 交换
    Swap(&arr[left], &arr[end - 1]);
    return left;
}
// 挖坑法
int64_t partion_Trenching(int arr[], int64_t beg, int64_t end)
{
    if(end - beg <= 1)
      return beg;
    int64_t left = beg;
    int64_t right = end - 1;
    int key = arr[end - 1];
    while(left < right)
    {
        // 从左往右找一个比 key 大的数
        while(left < right && arr[left] <= key)
          ++left;
        if(left < right)
          arr[right--] = arr[left];
        // 从右往左找一个比 key 小的数
        while(left < right && arr[right] >= key)
          --right;
        if(left < right)
          arr[left++] = arr[right];
    }
    // 退出循环,还剩最后一个坑
    arr[left] = key;
    return left;
}
void _QuickSort(int arr[], int64_t beg, int64_t end)
{
    if(end - beg <= 1)
      return ;
    //int64_t mid = partion_swap(arr, beg, end);
    int64_t mid = partion_Trenching(arr, beg, end);
    _QuickSort(arr, beg, mid);
    _QuickSort(arr, mid+1, end);
}
void QuickSort(int arr[], size_t size)
{
    if(size <= 1)
      return ;
    int64_t beg = 0;
    int64_t end = size;
    _QuickSort(arr, beg, end);
}
////////////////////////////////
// 测试代码
////////////////////////////////
void TestBubbleSort()
{
    TEST_HEAD;
    int arr[] = {9, 2, 4, 7, 5, 8, 3, 1, 6};
    int size = sizeof(arr)/sizeof(arr[0]);
    printf("[排序之前]\n");
    for(int i=0; i<size; i++)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
    BubbleSort(arr, size);
    printf("[排序之后]\n");
    for(int i=0; i<size; i++)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
}
void TestSelectSort()
{
    TEST_HEAD;
    int arr[] = {9, 2, 4, 7, 5, 8, 3, 1, 6};
    int size = sizeof(arr)/sizeof(arr[0]);
    printf("[排序之前]\n");
    for(int i=0; i<size; i++)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
    SelectSort(arr, size);
    printf("[排序之后]\n");
    for(int i=0; i<size; i++)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
}
void TestInsertSort()
{
    TEST_HEAD;
    int arr[] = {9, 5, 2, 7};
    int size = sizeof(arr)/sizeof(arr[0]);
    printf("[排序之前]\n");
    for(int i=0; i<size; i++)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
    InsertSort(arr, size);
    printf("[排序之后]\n");
    for(int i=0; i<size; i++)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
}
void TestHeapSort()
{
    TEST_HEAD;
    int arr[] = {9, 5, 2, 7};
    int size = sizeof(arr)/sizeof(arr[0]);
    printf("[排序之前]\n");
    for(int i=0; i<size; i++)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
    HeapSort(arr, size);
    printf("[排序之后]\n");
    for(int i=0; i<size; i++)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
}
void TestShellSort()
{
    TEST_HEAD;
    //int arr[] = {9, 5, 2, 7};
    int arr[] = {9, 2, 4, 7, 5, 8, 3, 1, 6};
    int size = sizeof(arr)/sizeof(arr[0]);
    printf("[排序之前]\n");
    for(int i=0; i<size; i++)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
    ShellSort(arr, size);
    printf("[排序之后]\n");
    for(int i=0; i<size; i++)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
}
void TestMergeSort()
{
    TEST_HEAD;
    //int arr[] = {9, 5, 2, 7};
    int arr[] = {9, 2, 4, 7, 5, 8, 3, 1, 6};
    int size = sizeof(arr)/sizeof(arr[0]);
    printf("[排序之前]\n");
    for(int i=0; i<size; i++)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
    //MergeSort(arr, size);
    MergeSortByLoop(arr, size);
    printf("[排序之后]\n");
    for(int i=0; i<size; i++)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
}
void TestQuickSort()
{
    TEST_HEAD;
    //int arr[] = {9, 5, 2, 7};
    int arr[] = {9, 2, 4, 7, 5, 8, 3, 1, 6};
    int size = sizeof(arr)/sizeof(arr[0]);
    printf("[排序之前]\n");
    for(int i=0; i<size; i++)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
    QuickSort(arr, size);
    printf("[排序之后]\n");
    for(int i=0; i<size; i++)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
}


int main()
{
    TestBubbleSort();
    TestSelectSort();
    TestInsertSort();
    TestHeapSort();
    TestShellSort();
    TestMergeSort();
    TestQuickSort();
    printf("\n");
    printf("\n");
    printf("\n");
    return 0;
}

这里写图片描述