迷宫求解
0 0 1 0 0 0
0 0 1 1 1 0
1 1 1 0 1 1
0 0 1 0 1 0
0 0 1 1 1 1
0 0 0 0 0 0
如上图所示的一个迷宫, 0为墙, 1为路, 编写程序求解
1) 求简单迷宫是否存在路径
2) 求多出口迷宫的最短路径
3) 求带环的多出口迷宫的最短路径
思路: 利用栈保存走过的点, 走不通时开始回溯, 直到找到出口
求简单迷宫是否存在路径
1, 递归版本
//迷宫求解
//思路: 从一个入口点开始, 依次判断它的 上,右,下,左 方位能不能走
// 如果能就直接走, 每走一步将这个位置的坐标入栈, 并且标记为2, 代表已经走过
// 若都不能走, 说明走到死路了, 要开始回溯
// 回溯时就是把入栈的坐标出栈, 即可原路返回, 每返回一步就重新再判断它的 上右下左 能不能走
// 直到找到出口
//方法一: 利用递归的函数调用栈, 保存已经走过的点
//方法二: 利用自己定义的栈, 保存已经走过的点
#include <stdio.h>
#define ROW 9
#define COL 9
//先定义一个迷宫地图
int map[ROW][COL] = {
{0, 0, 1, 0, 0, 0, 1, 0, 0},
{0, 0, 1, 0, 0, 0, 0, 0, 0},
{0, 0, 1, 0, 0, 1, 1, 1, 0},
{0, 0, 1, 0, 0, 1, 0, 0, 0},
{0, 0, 1, 1, 1, 1, 0, 1, 0},
{0, 0, 1, 0, 0, 1, 0, 1, 0},
{0, 0, 1, 0, 0, 1, 1, 1, 1},
{0, 0, 1, 0, 0, 1, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 0, 0},
};
//定义一个点
typedef struct point
{
int row;
int col;
}point;
//打印迷宫
void MazePrint(int map[][COL], char* msg)
{
printf("\n==========%s==========\n", msg);
if(map == NULL)
return ;
for(int i=0; i<ROW; i++)
{
for(int j=0; j<COL; j++)
{
printf("%2d ", map[i][j]);
}
printf("\n");
}
}
//一, 利用递归的函数调用栈
//判断能否落脚的函数
int canStay(point cur)
{
//点在地图外, 则不能走
if(cur.row < 0 || cur.col < 0 || cur.row > ROW || cur.col > COL)
{
//点越界
return 0;
}
//点的值是 0 或 2 则不能走
if(map[cur.row][cur.col] == 0 || map[cur.row][cur.col] == 2)
{
return 0;
}
//点的值是 1 则能走
if(map[cur.row][cur.col] == 1)
{
return 1;
}
}
//遍历判断 上右下左 能否落脚的函数
//point CW_Traversal(point cur)
//{
// //定义上右下左 4个点
// point up = {cur.row-1, cur.col};
// point right = {cur.row, cur.col+1};
// point down = {cur.row+1, cur.col};
// point left = {cur.row, cur.col-1};
//
// if( canStay(up) )
// {
// return up;
// }
// if( canStay(right) )
// {
// return right;
// }
// if( canStay(down) )
// {
// return down;
// }
// if( canStay(left) )
// {
// return left;
// }
// //如果都能落脚, 就返回当前点
// return cur;
//}
//标记
void Mark(point cur)
{
map[cur.row][cur.col] = 2;
}
//判读出口
int isExit(point cur, point entry)
{
//点的坐标在边界, 就说明是出口
//但是如果是入口, 肯定不是出口
if(cur.row == entry.row && cur.col == entry.col)
{
return 0;
}
else if(cur.row == 0 || cur.col == 0 || cur.row == ROW-1 || cur.col == COL-1)
{
return 1;
}
return 0;
}
//辅助递归
void assistRecursion(point now_cur, point entry)
{
//判断这个入口点能否落脚
if( canStay(now_cur) )
{
printf("cur : (%d, %d)\n", now_cur.row, now_cur.col);
//如果能落脚, 把这个点标记为 2
Mark(now_cur);
//判断是否为出口
if( isExit(now_cur, entry) )
{
//是出口, 直接返回
printf("找到了一条路径\n");
return ;
}
//遍历它的 上右下左 判断能否落脚
point up = {now_cur.row-1, now_cur.col};
assistRecursion(up, entry);
point right = {now_cur.row, now_cur.col+1};
assistRecursion(right, entry);
point down = {now_cur.row+1, now_cur.col};
assistRecursion(down, entry);
point left = {now_cur.row, now_cur.col-1};
assistRecursion(left, entry);
}
}
//寻找路径
void getPath(point entry)
{
//辅助递归函数
assistRecursion(entry, entry);
}
int main()
{
point entry = {0, 2};//定义入口
MazePrint(map, "打印迷宫");
getPath(entry);
MazePrint(map, "迷宫路线");
printf("\n\n\n");
printf("\n\n\n");
printf("\n\n\n");
return 0;
}
2, 非递归版本
//迷宫求解
//思路: 从一个入口点开始, 依次判断它的 上,右,下,左 方位能不能走
// 如果能就直接走, 每走一步将这个位置的坐标入栈, 并且标记为2, 代表已经走过
// 若都不能走, 说明走到死路了, 要开始回溯
// 回溯时就是把入栈的坐标出栈, 即可原路返回, 每返回一步就重新再判断它的 上右下左 能不能走
// 直到找到出口
//方法一: 利用递归的函数调用栈, 保存已经走过的点
//方法二: 利用自己定义的栈, 保存已经走过的点
#include <stdio.h>
#include <stdlib.h>
#include <memory.h>
// 9*9的迷宫
#define ROW 6
#define COL 6
//定义一个迷宫地图
int map[ROW][COL] = {
{0, 0, 1, 0, 0, 0 },
{0, 0, 1, 1, 1, 0 },
{1, 1, 1, 0, 1, 1 },
{0, 0, 1, 0, 0, 0 },
{0, 0, 1, 1, 1, 1 },
{0, 0, 0, 0, 0, 0 },
};
//定义一个坐标点
typedef struct point
{
int row;
int col;
}point;
//打印迷宫
void MazePrint(int map[][COL], char* msg)
{
printf("\n==========%s==========\n", msg);
if(map == NULL)
return ;
for(int i=0; i<ROW; i++)
{
for(int j=0; j<COL; j++)
{
printf("%2d ", map[i][j]);
}
printf("\n");
}
printf("\n");
}
//方法二: 利用自己定义的栈, 保存已经走过的点
#define MAX_SIZE 100
typedef point DataType;
typedef struct stack
{
//栈里保存的元素类型是一个结构体
DataType data[MAX_SIZE];
int size;
}stack;
//定义栈 并初始化
stack mystack;
stack now_path;
stack shortest_path;
//初始化栈
void stackInit(stack* stk)
{
stk->size = 0;
}
//入栈
void stackPush(stack* stk, DataType cur)
{
if(stk == NULL)
return ;
stk->data[stk->size] = cur;
stk->size++;
}
//出栈
void stackPop(stack* stk)
{
if(stk == NULL)
{
return ;
}
--stk->size;
}
//取栈顶元素
int stackTop(stack* stk, DataType* cur)
{
if(stk == NULL)
return 0;
if(cur == NULL)
return 0;
if(stk->size == 0)
return 0;
*cur = ( stk->data[stk->size-1] );
return 1;
}
//打印栈
void stackPrint(stack* stk, char* msg)
{
printf("\n========%s=======\n", msg);
if(stk == NULL)
return ;
for(int i=0; i<stk->size; i++)
{
printf("(%d, %d)\n", stk->data[i].row, stk->data[i].col);
}
printf("\n");
}
//判断能否落脚的函数
int canStay(point cur)
{
if(cur.row < 0 || cur.col < 0 || cur.row > ROW || cur.col > COL)
{
//点越界
return 0;
}
//点的值是 0 或 2 则不能走
if(map[cur.row][cur.col] == 0 || map[cur.row][cur.col] == 2)
{
return 0;
}
//点的值是 1 则能走
if(map[cur.row][cur.col] == 1)
{
return 1;
}
}
//遍历判断 上右下左 能否落脚的函数
//point CW_Traversal(point cur)
//{
// //定义上右下左 4个点
// point up = {cur.row-1, cur.col};
// point right = {cur.row, cur.col+1};
// point down = {cur.row+1, cur.col};
// point left = {cur.row, cur.col-1};
//
// if( canStay(up) )
// {
// return up;
// }
// if( canStay(right) )
// {
// return right;
// }
// if( canStay(down) )
// {
// return down;
// }
// if( canStay(left) )
// {
// return left;
// }
// //如果都能落脚, 就返回当前点
// return cur;
//}
//标记已经走过的点
void Mark(point cur)
{
map[cur.row][cur.col] = 2;
}
//判断当前点是不是出口
int isExit(point cur, point entry)
{
//如果是入口, 肯定不是出口
if(cur.row == entry.row && cur.col == entry.col)
return 0;
//除此之外
//点的坐标在边界, 就说明是出口
else if(cur.row == 0 || cur.col == 0 || cur.row == ROW-1 || cur.col == COL-1)
return 1;
return 0;
}
//获取路径辅助函数
void MazeSlove(point now_cur, point entrance)
{
//判断当前点能否落脚
if( canStay(now_cur) )
{
//如果能落脚, 把这个点标记为 2
Mark(now_cur);
//然后入栈
stackPush(&mystack, now_cur);
while(1)
{
point cur;
//取栈顶元素
int ret = stackTop(&mystack, &cur);
//打印出走过的坐标
printf("cur : (%d, %d)\n", cur.row, cur.col);
if(ret == 0)
{
//栈为空, 回溯结束了
return ;
}
//判断这个栈顶的点是不是出口
if( isExit(cur, entrance) )
{
//是出口,则说明找到了一条路线,直接返回
printf("找到了一条路线\n");
return ;
}
//上
point up = {cur.row-1, cur.col};
//先判断能否落脚
if( canStay(up) )
{
//标记为2
Mark(up);
stackPush(&mystack, up);
continue;
}
//右
point right = {cur.row, cur.col+1};
if( canStay(right) )
{
//标记为2
Mark(right);
stackPush(&mystack, right);
continue;
}
//下
point down = {cur.row+1, cur.col};
if( canStay(down) )
{
//标记为2
Mark(down);
stackPush(&mystack, down);
continue;
}
//左
point left = {cur.row, cur.col-1};
if( canStay(left) )
{
//标记为2
Mark(left);
stackPush(&mystack, left);
continue;
}
//如果4个点都不能走, 就让当前点出栈, 开始回溯
stackPop(&mystack);
}
}
}
//获取路径主函数
void getPath(point entry)
{
MazeSlove(entry, entry);
}
//路径替换函数
void replacePath(stack* dst, stack* src)
{
if(dst == NULL || src == NULL)
return ;
//先把 shortest_path 里的元素清空
//memset(dst, 0, sizeof(point)*src->size + 1);
dst->size = 0;
for(int i=0; i<src->size; i++)
{
dst->data[i] = src->data[i];
dst->size++;
//printf("(%d, %d)\n", dst->data[i].row, dst->data[i].col);
}
}
//求多出口迷宫的最短路径
void getShortestPath(point now_cur, point entry, stack* now_path, stack* shortest_path)
{
//判定当前点能否落脚
if( canStay(now_cur) )
{
Mark(now_cur);
stackPush(now_path, now_cur);
loop: while(1)
{
point cur;
int ret = stackTop(now_path, &cur);
if(ret == 0)
{
stackPrint(shortest_path, "最短路径");
//栈为空 回溯结束了
return ;
}
//判断当前点是不是出口
if( isExit(cur, entry) )
{
//找到一条路径以后, 拿它和 shortest_path 对比
//如果当前路径比 shortest_path 短, 或者 shortest_path 为空
//就用 now_path 替换 shortest_path
if( now_path->size < shortest_path->size || shortest_path->size == 0 )
{
//替换路径函数
replacePath(shortest_path, now_path);
}
//如果now_path 不比 shortest_path 更短
//则继续找其他路径
stackPop(now_path);
goto loop;
}
//如果当前点不是出口
//就遍历周围的 4 个点
//上
point up = {cur.row-1, cur.col};
//先判断能否落脚
if( canStay(up) )
{
//标记为2
Mark(up);
stackPush(now_path, up);
continue;
}
//右
point right = {cur.row, cur.col+1};
if( canStay(right) )
{
//标记为2
Mark(right);
stackPush(now_path, right);
continue;
}
//下
point down = {cur.row+1, cur.col};
if( canStay(down) )
{
//标记为2
Mark(down);
stackPush(now_path, down);
continue;
}
//左
point left = {cur.row, cur.col-1};
if( canStay(left) )
{
//标记为2
Mark(left);
stackPush(now_path, left);
continue;
}
//若4个点都不能落脚
stackPop(now_path);
}
}
}
void getShortestPath_main(point entry)
{
getShortestPath(entry, entry, &now_path, &shortest_path);
}
void TestReplace()
{
point cur1 = {1,2};
point cur2 = {1,3};
point cur3 = {1,4};
point cur4 = {1,5};
stackPush(&now_path, cur1);
stackPush(&now_path, cur2);
stackPush(&now_path, cur3);
stackPush(&now_path, cur4);
replacePath(&shortest_path, &now_path);
stackPrint(&now_path, "打印当前路径");
stackPrint(&shortest_path, "打印最短路径");
}
void TestShortestPath()
{
stackInit(&now_path);
stackInit(&shortest_path);
point entry = {0, 2};
MazePrint(map, "打印迷宫");
getShortestPath_main(entry);
MazePrint(map, "迷宫路线");
}
void TestGetPath()
{
stackInit(&mystack);
point entry = {0, 2};//定义入口
MazePrint(map, "打印迷宫");
getPath(entry);
MazePrint(map, "迷宫路线");
}
int main()
{
//TestGetPath();
//TestReplace();
TestShortestPath();
printf("\n\n\n");
printf("\n\n\n");
printf("\n\n\n");
return 0;
}
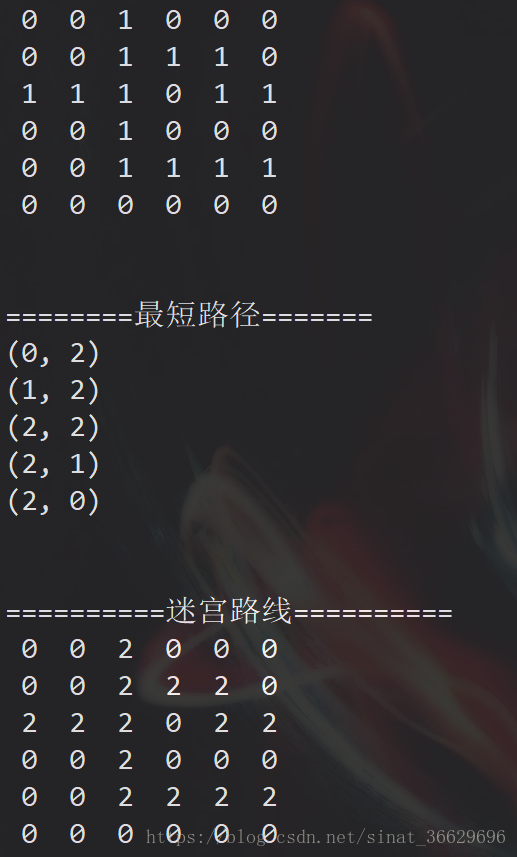
但是如果迷宫带环, 上面的方法就会出问题了
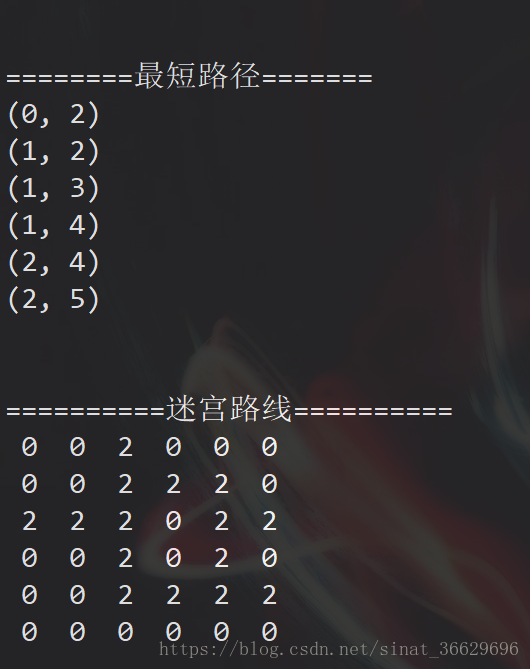
这时, 求出了错误的结果, 所以我们需要改变一些规则
请看下面的带环求多出口迷宫的最短路径方法
求带环的多出口迷宫的最短路径
//迷宫求解
//思路: 从一个入口点开始, 依次判断它的 上,右,下,左 方位能不能走
// 如果能就直接走, 每走一步将这个位置的坐标入栈, 并且标记为2, 代表已经走过
// 若都不能走, 说明走到死路了, 要开始回溯
// 回溯时就是把入栈的坐标出栈, 即可原路返回, 每返回一步就重新再判断它的 上右下左 能不能走
// 直到找到出口
//方法一: 利用递归的函数调用栈, 保存已经走过的点
//方法二: 利用自己定义的栈, 保存已经走过的点
#include <stdio.h>
#include <stdlib.h>
#include <memory.h>
// 9*9的迷宫
#define ROW 6
#define COL 6
//定义一个迷宫地图
int map[ROW][COL] = {
{0, 0, 1, 0, 0, 0 },
{0, 0, 1, 1, 1, 0 },
{1, 1, 1, 0, 1, 1 },
{0, 0, 1, 0, 1, 0 },
{0, 0, 1, 1, 1, 1 },
{0, 0, 0, 0, 0, 0 },
};
//定义一个坐标点
typedef struct point
{
int row;
int col;
}point;
//打印迷宫
void MazePrint(int map[][COL], char* msg)
{
printf("\n==========%s==========\n", msg);
if(map == NULL)
return ;
for(int i=0; i<ROW; i++)
{
for(int j=0; j<COL; j++)
{
printf("%2d ", map[i][j]);
}
printf("\n");
}
printf("\n");
}
//方法二: 利用自己定义的栈, 保存已经走过的点
#define MAX_SIZE 100
typedef point DataType;
typedef struct stack
{
//栈里保存的元素类型是一个结构体
DataType data[MAX_SIZE];
int size;
}stack;
//定义栈 并初始化
stack mystack;
stack now_path;
stack shortest_path;
//初始化栈
void stackInit(stack* stk)
{
stk->size = 0;
}
//入栈
void stackPush(stack* stk, DataType cur)
{
if(stk == NULL)
return ;
stk->data[stk->size] = cur;
stk->size++;
}
//出栈
void stackPop(stack* stk)
{
if(stk == NULL)
{
return ;
}
--stk->size;
}
//取栈顶元素
int stackTop(stack* stk, DataType* cur)
{
if(stk == NULL)
return 0;
if(cur == NULL)
return 0;
if(stk->size == 0)
return 0;
*cur = ( stk->data[stk->size-1] );
return 1;
}
//打印栈
void stackPrint(stack* stk, char* msg)
{
printf("\n========%s=======\n", msg);
if(stk == NULL)
return ;
for(int i=0; i<stk->size; i++)
{
printf("(%d, %d)\n", stk->data[i].row, stk->data[i].col);
}
printf("\n");
}
//判断能否落脚的函数
int canStay(point cur)
{
if(cur.row < 0 || cur.col < 0 || cur.row > ROW || cur.col > COL)
{
//点越界
return 0;
}
//点的值是 0 或 2 则不能走
if(map[cur.row][cur.col] == 0 || map[cur.row][cur.col] == 2)
{
return 0;
}
//点的值是 1 则能走
if(map[cur.row][cur.col] == 1)
{
return 1;
}
}
//标记已经走过的点
void Mark(point cur)
{
map[cur.row][cur.col] = 2;
}
//判断当前点是不是出口
int isExit(point cur, point entry)
{
//如果是入口, 肯定不是出口
if(cur.row == entry.row && cur.col == entry.col)
return 0;
//除此之外
//点的坐标在边界, 就说明是出口
else if(cur.row == 0 || cur.col == 0 || cur.row == ROW-1 || cur.col == COL-1)
return 1;
return 0;
}
//路径替换函数
void replacePath(stack* dst, stack* src)
{
if(dst == NULL || src == NULL)
return ;
//先把 shortest_path 里的元素清空
//memset(dst, 0, sizeof(point)*src->size + 1);
dst->size = 0;
for(int i=0; i<src->size; i++)
{
dst->data[i] = src->data[i];
dst->size++;
//printf("(%d, %d)\n", dst->data[i].row, dst->data[i].col);
}
}
//canStayWithCycle 带环判定落脚函数
int canStayWithCycle(point now_cur, point pre_cur)
{
//点在地图外 不能落脚
if(now_cur.row < 0 || now_cur.col < 0 || now_cur.row > ROW || now_cur.col > COL)
{
return 0;
}
//取now_cur的值
int now_cur_value = map[now_cur.row][now_cur.col];
//如果 now_cur_value 是 0, 则不能走
if(now_cur_value == 0)
{
return 0;
}
//如果 now_cur_value 是1, 则可以直接走
if(now_cur_value == 1)
{
return 1;
}
//now_cur的值大于pre_cur的值 + 1, 则能走
else
{
int pre_cur_value = map[pre_cur.row][pre_cur.col];
if(now_cur_value > pre_cur_value + 1)
{
return 1;
}
return 0;
}
}
//带环标记函数
void markWithCycle(point now_cur, point pre_cur, point entry)
{
//如果当前点是入口, 直接标记为2
if(now_cur.row == entry.row && now_cur.col == entry.col)
{
map[now_cur.row][now_cur.col] = 2;
}
else
{
//当前点应该标记为它的上一个点的值 + 1
map[now_cur.row][now_cur.col] = map[pre_cur.row][pre_cur.col] + 1;
}
}
//求带环的多出口迷宫的最短路径
void getShortestPathWithCycle(point now_cur, point pre_cur, point entry, stack* now_path, stack* shortest_path)
{
//判定当前点能否落脚(判定规则改变了)
if( canStayWithCycle(now_cur, pre_cur) )
{
//标记当前点(规则也变了)
markWithCycle(now_cur, pre_cur, entry);
//当前点入栈
stackPush(now_path, now_cur);
loop: while(1)
{
point cur;
int ret = stackTop(now_path, &cur);
if(ret == 0)
{
stackPrint(shortest_path, "最短路径");
//栈为空 回溯结束了
return ;
}
pre_cur = cur;
//判断当前点是不是出口(规则没变)
if( isExit(cur, entry) )
{
//找到一条路径以后, 拿它和 shortest_path 对比
//如果当前路径比 shortest_path 短, 或者 shortest_path 为空
//就用 now_path 替换 shortest_path
if( now_path->size < shortest_path->size || shortest_path->size == 0 )
{
//替换路径函数
replacePath(shortest_path, now_path);
}
//则继续找其他路径
stackPop(now_path);
goto loop;
}
//如果当前点不是出口
//就遍历周围的 4 个点
//上
point up = {cur.row-1, cur.col};
//先判断能否落脚
if( canStayWithCycle(up, pre_cur) )
{
//标记
markWithCycle(up, pre_cur, entry);
stackPush(now_path, up);
continue;
}
//右
point right = {cur.row, cur.col+1};
if( canStayWithCycle(right, pre_cur) )
{
//标记
markWithCycle(right, pre_cur, entry);
stackPush(now_path, right);
continue;
}
//下
point down = {cur.row+1, cur.col};
if( canStayWithCycle(down, pre_cur) )
{
//标记
markWithCycle(down, pre_cur, entry);
stackPush(now_path, down);
continue;
}
//左
point left = {cur.row, cur.col-1};
if( canStayWithCycle(left, pre_cur) )
{
//标记
markWithCycle(left, pre_cur, entry);
stackPush(now_path, left);
continue;
}
//若4个点都不能落脚
stackPop(now_path);
}
}
}
void getShortestPath_main(point entry)
{
point pre_cur = {-1, -1};
getShortestPathWithCycle(entry, pre_cur, entry, &now_path, &shortest_path);
}
void TestShortestPath()
{
stackInit(&now_path);
stackInit(&shortest_path);
point entry = {0, 2};
MazePrint(map, "打印迷宫");
getShortestPath_main(entry);
MazePrint(map, "迷宫路线");
}
int main()
{
TestShortestPath();
printf("\n\n\n");
printf("\n\n\n");
printf("\n\n\n");
return 0;
}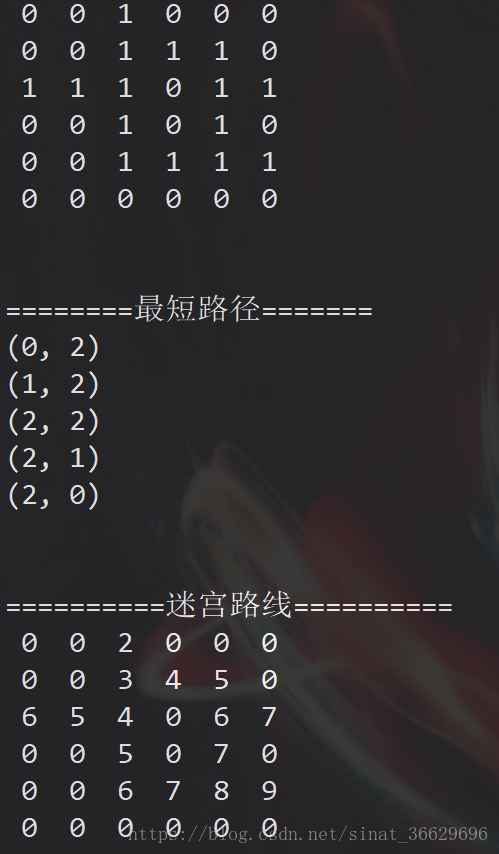
此时每个出口的值 - 1, 便是从入口到出口走的步数
可以看出, 最短的走了 5 步, 打印出的路线也正确























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








