-
分布分析:
-
揭示数据的分布特征和分布类型。
-
|
数据类型 |
需求 |
图表 |
|
定量数据 |
分布形式(对称、非对称) 发现特大(特小)可疑值 |
频率分布表 频率分布直方图 茎叶图 |
|
定性分类数据 |
分布情况 |
饼图、条形图 |
-
对比分析:
-
把两个相互联系的指标进行比较,从数量上展示和说明研究对象规模的大小、水平的高低,速度的快慢,以及各种关系是否协调。特别适用于指标间的横纵向比较、时间序列的比较分析。在对比分析中,选择合适的对比标准是十分关键的步骤,只有选择合适,才能做出客观的评价。
-
对比分析方式
-
绝对数比较
-
相对数比较
-
结构相对数
-
比例相对数
-
比较相对数
-
强度相对数
-
计划完成程度相对数
-
动态相对数
-
-
-
-
统计量分析
-
用统计指标对定量数据进行统计描述,常从集中趋势和离中趋势两个方面进行分析
-
集中趋势度量 |
平均水平的指标是对个体集中趋势的度量,使用最广泛的是均值和中位数; | |
集中趋势度量 |
定义 |
公式 |
|
均值 |
所有数的平均值 |
原始计算公式:
加权均值(反应均值中不同重要程度):
|
|
中位数 |
将一组观察值按从小到大排列,位于中间的数 |
当N为奇数时:
当N为偶数时:
|
|
众数 |
数据集中出现最频繁的值 |
众数不具有唯一性 众数一般用于离散型变量而非连续型变量 |
离中趋势度量 |
对个体离开平均水平的度量是反应变异程度的指标,使用较广泛的是标准差(方差)、四分位间距 | |
离中趋势度量 |
定义 |
公式 |
|
极差 |
对数据集的极端值非常敏感,并且忽略了位于最大值与最小值之间的数据分布情况 |
极差=最大值-最小值 |
|
标准差 |
度量数据偏离均值的程度 |
|
|
变异系数 |
度量标准差相当于与均值的离中趋势 主要用来比较两个或多个具有不同单位或不同波动幅度的数据集的离中趋势 |
|
|
四分位间距 |
将所有数值由小到大排列并等分成四份,处于第一个分割点位置的数值为下四分位数,处于第二个分割点位置(中间位置)的是中位数,处于第三个分割点的数值是上四分位数 |
四分位间距,是上四分位数与下四分位数之差,期间包含了全部观察值的一半,其值越大,说明数据的变异程度越大;反之,说明变异程度小。 |
-
周期性分析
-
探索某个变量是否随着时间变化而呈现出某种周期变化趋势。
-
年(季度、月、周、天、时)周期趋势
-
-
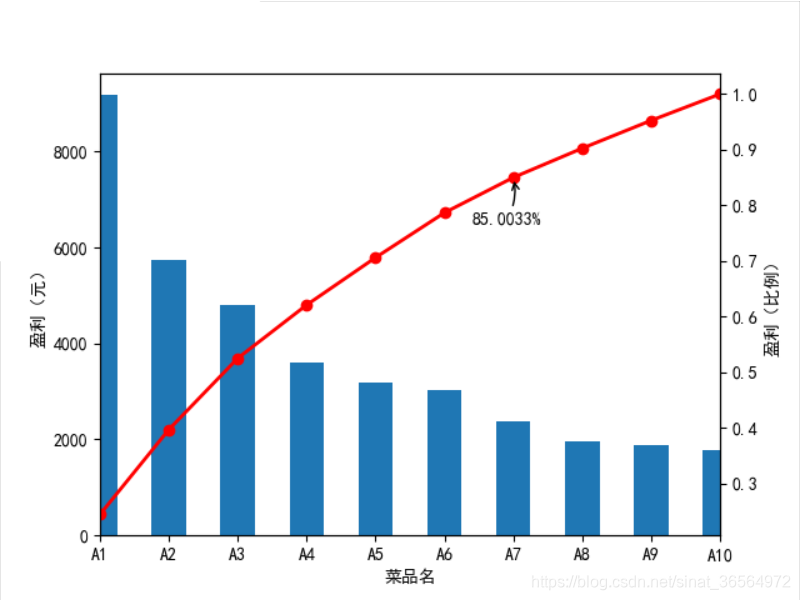
贡献度分析(帕累托分析)
-
原理:帕累托法则(20/80定律)。即同样的投入放在不同的地方会产生不同的效益。例如,一个公司80%的利润来自于20%最畅销的产品。
-
-
帕累托图实例:
#-*- coding: utf-8 -*-
#菜品盈利数据 帕累托图
from __future__ import print_function
import pandas as pd
#初始化参数
dish_profit = 'data/catering_dish_profit.xls' #餐饮菜品盈利数据
data = pd.read_excel(dish_profit, index_col = u'菜品名')
data = data[u'盈利'].copy()
data.sort_values(ascending = False)
import matplotlib.pyplot as plt #导入图像库
plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
plt.figure()
data.plot(kind='bar')
plt.ylabel(u'盈利(元)')
p = 1.0*data.cumsum()/data.sum()
p.plot(color = 'r', secondary_y = True, style = '-o',linewidth = 2)
plt.annotate(format(p[6], '.4%'), xy = (6, p[6]), xytext=(6*0.9, p[6]*0.9),
arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
#添加注释,即85%处的标记。这里包括了指定箭头样式。
plt.ylabel(u'盈利(比例)')
plt.show()
运行结果:
-
相关性分析
-
分析连续变量之间线性相关程度的强弱,并用适当的统计指标表示出来。
-
|
分析方法 |
内容 |
公式或图像 |
|
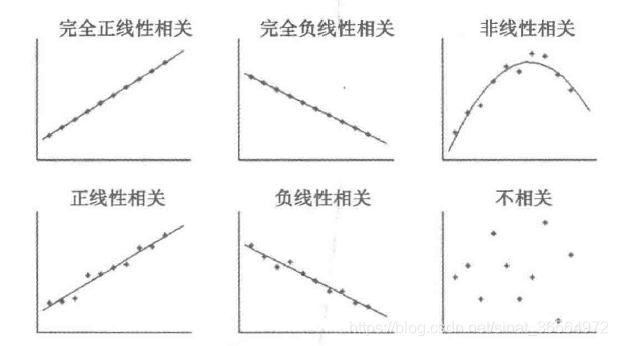
直接绘制散点图 |
判断两个变量是都具有线性相关关系最直观得方法是绘制散点图 |
|
|
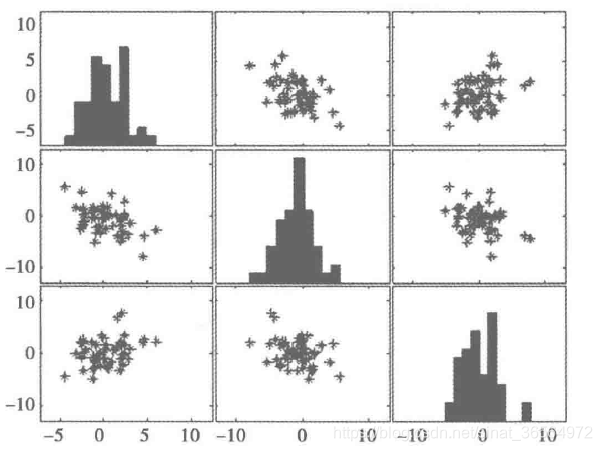
绘制散点图矩阵 |
同时考察多个变量间的相关关系时,可以利用散点图矩阵同时绘制各变量间的散点图。 在进行多元线性回归时显得尤为重要 |
|
|
计算相关系数 |
|
|
|
Pearson相关系数 (皮尔森相关系数) |
用于分析两个连续变量之间的关系(要求连续变量的两个取值服从正态分布): 相关系数r的取值范围: -1<=1<=1
|
|
|
Spearman秩相关系数 (斯皮尔曼相关系数) |
不服从正态分布的变量、分类或等级变量间的关联性可采用Spearman秩相关系数,也称等级相关系数。
只要两个变量具有严格单调的函数关系,那么它们就是完全Spearman相关的。 |
对两个变量成对的取值分别按照从小到大(或从大到小)顺序编秩, |
|
判定系数 |
判定系数是相关系数的平方,用 |
判定系数取值范围: 0<= |





 本文全面解析数据统计分析的核心方法,涵盖分布分析、对比分析、统计量分析、周期性分析、贡献度分析、相关性分析等内容,深入探讨各类数据分析手段的应用场景与计算公式。
本文全面解析数据统计分析的核心方法,涵盖分布分析、对比分析、统计量分析、周期性分析、贡献度分析、相关性分析等内容,深入探讨各类数据分析手段的应用场景与计算公式。
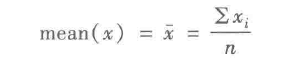
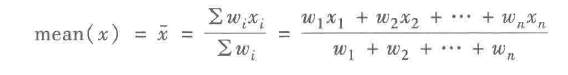
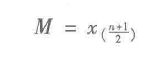
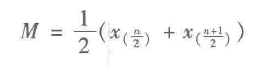
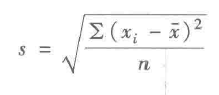
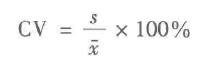

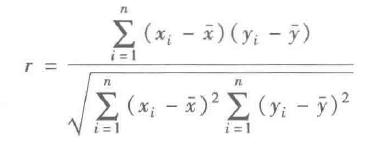

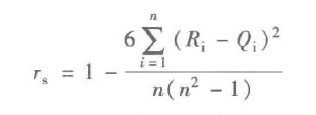
















 1215
1215

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








